2014-02-24
1504
Показательная форма записи комплексного числа.
Воспользовавшись тем, что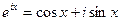 
, запишем комплексное число z
.
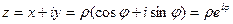После первого знака равенства стоит алгебраическая, после второго знака равенства – тригонометрическая, а после третьего знака равенства – показательная форма записи комплексного числа. При этом в показательной форме записи вновь явным образом указаны модуль и аргумент комплексного числа.
Теперь рассмотрим уравнение: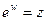 
и решим его относительно w: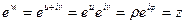 
.
Здесь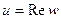 
, 
, 
, 
.
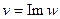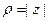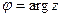Тогда: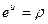 
, 
Þ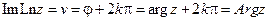 
.
Значит: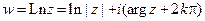 
, 
.
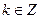Получена формула для вычисления логарифма комплексного числа. Отметим что, любое комплексное число (кроме нуля) имеет логарифм, причем этих значений бесконечно много.
Примеры:
1°.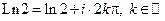 
;
2°.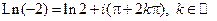 
.
И, наконец, можно ввести операцию возведения комплексного числа (не равного нулю) в произвольную комплексную степень: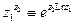 
.
Примеры:
1°.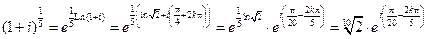 
.
2°.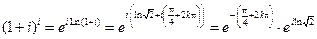 
.
3°.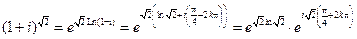 
.
4°.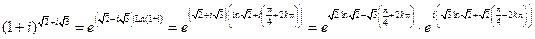 
.
5°.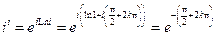 
.
6°.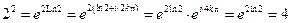 
.
*. Во всех решениях: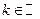 
.
Сделаем несколько замечаний, касающихся приведенных выше решений.
*. В задаче 1 получено пять различных решений расположенных на окружности радиуса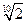 
в вершинах правильного пятиугольника.
*. В задаче 2 бесконечно много решений. Все они расположены на луче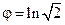 
и по модулю образуют бесконечную в обе стороны геометрическую последовательность со знаменателем 
.
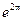*. В задаче 3 все решения расположены на окружности радиуса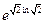 
и покрывают ее всюду плотным образом.
*. В задаче 4 решения расположены на спирали и всюду плотным образом заполняют направления в которых они находятся.
*. Задача 5. Удивительный факт: чисто мнимое число в чисто мнимой степени есть бесконечное множество вещественных положительных чисел.
*. Задача 6. И все таки дважды два равно четыре.
