2014-02-24
425
Рассматривается задача интегрирования рациональной дроби: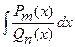 
.
а) Если m > n: т.е. дробь под знаком интеграла неправильная. Производя деление, получим
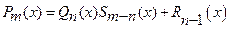Þ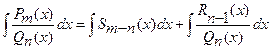 
,
причем:
*. Интеграл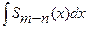 
легко берется (интеграл от полинома);
*. Интеграл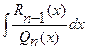 
- является интегралом от правильной дроби.
б) Разложим многочлен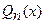 
на неприводимые множители, т.е. на линейные множители и квадратные трехчлены с вещественными коэффициентами без вещественных корней. Это всегда можно сделать, если у исходного многочлена вещественные коэффициенты:
(*)
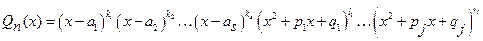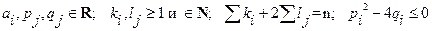
в) Метод разложения дроби на простейшие.
Теорема: Правильная дробь 
, у которой знаменатель 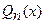представлен в виде (*) всегда может быть представлена в виде суммы элементарных дробей вида I, II, III, IV.
Т.е.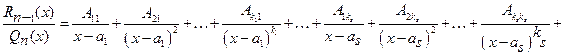 
.
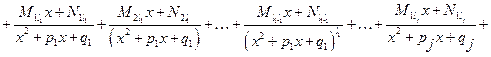
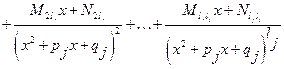Учитывая, что в правой части стоят только дроби I, II, III и IV типов, а интегрировать эти дроби мы научились, то задача интегрирования рациональной дроби решена.
Неопределенный интеграл от рациональной функции существует на любом промежутке, где знаменатель интегрируемой дроби не обращается в ноль и выражается через рациональные функции, логарифмы и арктангенсы в конечном виде.
