Groups, their main characteristics and the role of the personality in the group

M2 n2

N

И

X

A

X

-3

-1

X

X

2 7

X1

ЕЕ

X2

X1

A

0.

-6 6 6 -6

3 6 6 3

X2

nn

j =1

y 2 .. yn

= A

x_n

Или сокращенно

Y = AX.

Матрицу A называют матрицей оператора A в данном базисе.

Рангом оператора A называют ранг ее матрицы.

Суммой операторов A и В называют оператор, действующий по правилу

{A + В)x ¯ = Ax ¯ + Вx ¯ .

Произведением операторов A и В называют оператор, действующий по правилу

{AВ)x ¯ = A{Вx ¯ ).

Теорема 28. Сумме и ироизведению операторов соответствуют сумма и произведе­ние их матриц.

Нулевым называют оператор, который все векторы переводит в ноль. Ему соот­ветствует нулевая матрица.

Тоснсдественным называют оператор, который все векторы переводит в себя. Ему соответствует единичная матрица.

August 31, 2013 Курбатов В.Г. 43

5.3 Собственные значения и собственные векторы

Число λ и ненулевой вектор b называют, соответственно, собственным значением и собственным вектором квадратной матрицы A, если

A ¯ b = λ ¯ b. (5.2)

Равенство (5.2) моясно иеренисать в матричном виде

A ¯ b = λE ¯ b или (A - λE) ¯ b = ¯0,

где ¯ b — матрица-столбец, составленная из координат вектора ¯ b.

Теорема 29. Собственные значения матрицы A совпадают с корнями характери­стического уравнения

|A-λE| = 0.

Таким образом, чтобы найти собственные значения λ, нуясно решить уравнение

|A-λE| = 0, (5.3)

а чтобы найти собственные векторы, надо решить уравнение

(A - λE)b = 0.

Если определитель раскрыть, то получится многочлен степени n относительно λ. Такое уравнение имеет не более n решений. Для каждого решения λ моясно найти соответствующий ему собственный вектор ¯ b.

Задача 26. Найти собственные значения и собственные векторы оператора, заданного матрицей

A = 6 3 Решение. Составим характеристическое уравнение и решим его: A λE /3 6\ λ /1 0\ /3 6\ / λ 0

3 -λ 6 6 3 -λ

3 -λ 6 6 3 -λ

= (3 - λ)2 - 62 = 0 ,

(3 -λ- 6)(3 -λ + 6) = 0, (- 3 -λ)(9 -λ) = 0.

Получили два собственных значения λ 1 = - 3, λ 2 = 9. Теперь для каж;дого λ ^ найдем соответствуюш,ий ему собственный вектор.

August 31, 2013 Курбатов В.Г.

1. Для λ ₁ = - 3 составим уравнение (A - λE) ¯ b = 0:

1 0 0 1

6 6 6 6

Обозначим координаты собственного вектора b 1 через {x;y). Для них

6 6 6 6

6x 6x

6 y 6y

(A-λ1E)b1 =

Приравнивая к нулю, получим систему уравнений

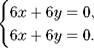
Прямой ход метода Гаусса

6 6 6 6

0 0 6x

(6 6 I 0)

приводит к одному уравнению

6 y = 0.

Полоясим y = C (т. е. примем y в качестве свободной неизвестной, см. § 2.8). Тогда все решения можно описать формулами x = С, y = C. Таким образом, все собственные векторы описываются формулой b 1 = {-; C) или b 1 = C (- 1; 1).

Решение однородной системы всегд - строено подобным образом. Поэтому обыч­но ограничиваются нахождением одного собственного вектора, т. е. одного нетриви­ального решения системы (A - λ1E)b = 0. Для этого вместо того, чтобы взять y = C полагают, что y есть некоторое фиксированное ненулевое число. Например, полагают y = 1. Тогда, повторяя предыдущие выкладки, приходят к ответу: b 1 = (- 1; 1).

2. Для λ ₂ = 9 имеем

A-λE =

1 0 0 1

В результате получаем систему уравнений

6x + 6 y = 0, 6x - 6y = 0.

C, тогда и

Опять система сводится к одному уравнению 6x - 6y = 0. Полож;им y x = C.В итоге ¯ b 2 = C (1;1).

3 и λ 2 = 9. П

Таким образом, матрица A имеет два собственных значения λ ₁ = Им отвечают собственные векторы b1 = (- 1;1) и ¯ b ₂ = (1;1)-

Теорема 30. Матрица оператора A в базисе, состоящем из собственных векторов

b1, ¯ b 2, • • •; bn диагональна:

λ 1 0

0 0

λ 2 .

λn

причем по диагонали стоят собственные значения.

Глава 6

Квадратичные формы

6.1 Определение квадратичной формы, ее матрица

Квадратичной формой называют функцию n неременных, имеющую вид

i=1 j=1

a_ijx_ix_j.

Здесь aij — заданные числа, называемые коэффициентами. Моясно считать, что a aji. Пример:

ij

L(x1,x2,x3) = 2x ²₁ ~ 5 x 1 x 2 + 4 x ²2 — 7x ²₃ + 2 x1x3 — 8 x 2 x 3.

Матрицу A, состоящую из коэффитщентов a_ij, называют матрицей квадратичной формы.

Задача 27. Дана квадратичная форма

L(x1,x2) = 3x ²₁ ~ 5 x 1 x 2 + 4x ²₂.

Выписать ее матрицу.

Решение. Запишем квадратичную форму в симметричном виде: L(x1,x2) = 3 x ²₁ — ⁵ x 1 x 2 — ⁵ x 2 x 1 + 4x2- Теперь легко написать матрицу:

A

⁵ ₂ 4

Теорема 31. Всякую квадратичную форму моукно представить в матричном виде

L = X'AX,

где

X =

И. обратно, всякая функция вида L = X'AX является квадратичной формой.

August 31, 2013 Курбатов В.Г.

Доказательство. Имеем

X'AX = (x1 x2... x_n

a 21 a 22

an 1 an 2

a 1 n a 2 n

x ₁ x ₂

x_n

i =1 j =1

a_ijx_ix_j.

Пусть столбцы переменных

X

x2 x_n

Y

y ₁

y2 y_n

связаны линейным преобразованием X = CY, где C — матрица, состоящая из за­данных чисел cij. Выполняя в представлении L = X'AX замену X = CY, приходим к представлению

L = X'AX = (CY)'ACY = Y'C'ACY = Y'(C'AC)Y.

Видно, что получилась квадратичная форма относительно переменных y ₁, y2, ■ ■ ■, y_n, имеющая матрицу CAC. Тем самым доказана

Теорема 32. При линейной замене X = CY матрица квадратичной формы преоб­разуется по правилу

A = C AC.

Если матрица C невырождена (т. е. det C = 0), то ранги матриц A я A = CAC совпадают. Ранг этих матриц называют рангом квадратичной формы.

Пример 26. Мы знаем, что ранг единичной матрицы

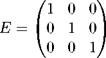
равен 3. Эта матрица порождает квадратичную форму L = x ²₁ + x2 + x ²₃ ранга 3.

6.2 Канонический вид и закон инерции

Говорят, что квадратичная форма имеет канонический вид, если ее матрица яв­ляется диагональной. В этом случае

L = a ₁₁ x ²₁ + a ₂ x ²₂ + ··· + a_nnx ² _n.

August 31, 2013 Курбатов В.Г. 47

Теорема 33. Любая квадратичная форма с помощью невыроукденного преобразо­вания X = CY приводится к капопическому виду.

Доказательство. Проведем на примере:

L = x ²₁ - 6 x 1 x 2 + 8 x 1 x ₃ + 5 x 2 - 16 x 2 x 3 + 10x ²₃ = = x ²₁ + 2 x 1(- 3 x 2 + 4 x ₃) + 5 x ² - 16 x 2 x 3 + 10x ²₃ =

x1 + (- 3 x 2 + 4 x 3)) -

- 3 x 2 + 4 x 3)2 + 5 x 2 - 16 x 2 x 3 + 10 x ²₃ =

x1 - 3 x 2 + 4 x ₃) - 4x ²₂ + 8 x 2 x 3 - 6 x ²3

x1 - 3 x 2 + 4 x ₃) - 4(x ²2 - 2 x 2 x 3) - 6x ²₃ x1 - 3 x 2 + 4 x ₃) - 4(x 2 - x ₃)² + 4 x ²₃ - 6 x 3

x1 - 3 x2 + 4 x ₃) - 4(x 2 - x ₃)² - 2 x ²₃.

Видно, что замена y ₁ = x ₁ - 3x2 + 4 x 3, y2 = x2 - x3, y4 = x3 (с треугольной матрицей)
приведет квадратичную форму к каноническому виду. П

Одна и та же квадратичная форма может быть преобразована к различным ка­ноническим видам. Общим во всех этих представлениях является только свойство, описываемое в следующей теореме.

Теорема 34 (закон инертщи). Число слагаемых с полоукительными (отрицатель­ными, пулевыми) коэффициентами пе зависит от способа приведения квадратичной формы к каноническому виду.

Следствие 35. Ранг квадратичной формы равен числу ненулевых слагаемых в лю­бом ее каноническом нредставленип.

6.3 Знакоопределенные квадратичные формы

Из формулы

^{n n}

L = у ^ у ^ aijxixj.

i=1 j=1

ВИДНО, что при x1 = x2 = • • • = x_n = 0 любая квадратичная форма L равна нулю. Квадратичную форму называют

Ф положительно определенной, если

L(x1, x2,..., x_n) > 0,

при условии, что вектор (x 1 ,x 2 ,...,x_n) отличен от нуля,

Ф отрицательно определенной, если

L(x1,x2,...,x_n) < 0,

если хотя бы один аргумент x1, x2,..., x_n отличен от нуля,

August 31, 2013 Курбатов В.Г.

Ф знакопеременной, если она принимает как положительные, так и отрицатель­ные значения.

Очевидно, факт знакоонределенности не меняется при замене переменных X = CY. Для канонической формы

L = a11x ²₁ + a 2 x ²2

+ anrix.

положительная (отрицательная) определенность, очевидно, означает, что все коэф­фициенты aц положительны (отрицательны). А знаконеременность — что есть как положительные, так и отрицательные коэффициенты.

Теорема 36. Для того чтобы квадратичная форма была полож.ителвно (отрица-телвно) определенной, необходимо и достаточно, чтобы все собственивте значения ее матрицы бв1ли нолож.ителвнв1ми (отрнцателвивтми).

Теорема 37 (критерий Сильвестра). Для того чтобы квадратичная форма была иолоукителвно оиределенной, необходимо и достаточно, чтобвт все главивхе минорв!

∆1 = a 11, ∆2

a 11 a 12 a 21 a 22

∆

a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33

ее матритщ бвтли иолож.ителвнв1.

Задача 28. Доказать, что квадратичная форма L = 1 3 x ²₁ — 4 x 1 x 2 + 7x ²₂ положительно определена.

Решение. Выпишем матрицу квадратичной формы:

I. Собственные значения этой матрицы равны 5 и 15. Поэтому по теореме 36

квадратичная форма полож;ительпо определена.

П. a 11 = 13 > 0, тельпо определена.

13 —2

75 > 0. По теореме 37 квадратичная форма положи-

Глава 7

Элементы аналитической геометрии

7.1 Уравнение линии на плоскости

с интуитивной точки зрения линия — это след, оставляемый двиясущейся точкой.

Уравнением линии называют уравнение, которому удовлетворяют координаты каясдой точки, нринадлеясащей данной линии, но не удовлетворяют координаты лю­бой точки, не иринадлеясатдей данной линии. Например, y = x"^, x^ + y^ = 1.

Правило: Чтобы проверить, иринадлеясит ли точка липни, надо координаты точки подставить в уравнение линии.

Различают два тина уравнений:

y = f (x), (7.1)

F (x,y) = 0. (7.2)

Примеры таких уравнений:

y = e^x, x ^ + y ^ = 1.

В уравнении (7.1) неизвестная y явно выраясена через x. Такой способ задания назы­вают явным. Чтобы, зная x, с помощью уравнения (7.2) найти y, надо это уравнение решить. Такой способ задания называют неявным.

Правило: чтобы найти точку (точки) пересечения двух линий, надо выписать систему, состоящую из уравнений этих линий, и решить ее.-*-)

7.2 Уравнение прямой с угловым коэффициентом

Уравнением прямой с угловым коэффициентом называют уравнение вида

y = kx + b.

В нем коэффициент k имеет геометрический смысл тангенса угла меясду осью X и прямой.^) Число k называют угловым коэффициентом прямой. Если k > 0, то

August 31, 2013 Курбатов В.Г.

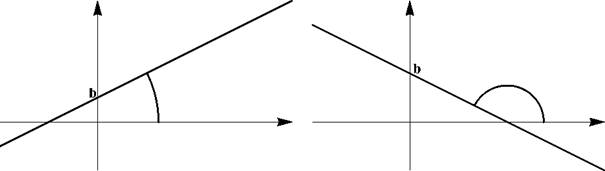
Рис. 1: Слева: k > 0; справа k < 0

график прямой возрастает. А если k < 0, то график прямой убывает. Число b имеет геометрический смысл координаты точки пересечения прямой с осью Y.

Правило: Угловой коэффициент — это то, па что умножается x в явном уравне­нии прямой. Примеры: 2 y + 4 x = 6 и y = —2x + 3.

■•■^Часто это правило формулирует не виолне корректно: надо приравнять у. Это путь можно реализовать только при условии, что оба уравнения являются явными. ■^Ютсчитываемого в нанравлении от оси к прямой.

August 31, 2013 Курбатов В.Г.

Задача 29. Составьте уравнение прямой, проходящей через заданную точку (xо,yо) с заданным угловым коэффициентом k.

Решение. Ответом является уравнение

y - y ₀ = k (x - x ₀).

Эту формулу надо знать наизусть.

7.3 Общее уравнение прямой

Не все прямые можно задать уравнением с угловым коэффициентом. А именно, исключением является вертикальная прямая (см. рис. 2):

x = a.

Общим уравнением прямой называют уравнение

Ax + By + C = 0

в предположении, что хотя бы одно из чисел A, B не равно нулю. Это уравнение охватывает все типы прямых.

Рис. 2: Вертикальная прямая

7.4 Уравнение прямой,

проходящей через две заданные точки

Задача 30. Составьте уравнение прямой, проходящей через две заданные точки (xо,yо) и (xi,yi).

August 31, 2013 Курбатов В.Г.

Решение. Ответом является уравнение

y -y 0

x-x ₀

y ₁ -y ₀ x ₁ -x ₀

Универсальный способ построения прямых: надо нарисовать две точки, лежащие на прямой, и провести через них прямую.

7.5 Условие параллельности

и перпендикулярности прямых

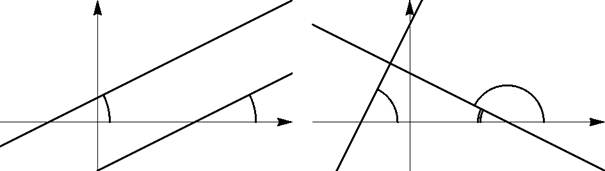
Теорема 38. Пусть даны две прямые y = kix + bi и y = k2x + b ₂- Для того чтобы эти прямые были параллельны, необходимо и достаточно, чтобы

k ₁ = k ₂.

Для того, чтобы прямые были перпеидикуляриы, необходимо и достаточно, чтобы

k ₁ k ₂

1.

Рис. 3: Идея доказательства теоремы 38

Задача 31. Дана прямая 2 y + 3 x —7 = 0. Составьте уравнения двух прямых, проходя­щих через точку (5,9), одна из которых параллельна, а другая — перпендикулярна исходной.

Решение. Выясним, какой угловой коэффициент у исходной прямой: (Угловой ко­эффициент — это то, на что умножается x в явном уравнении прямой.)

37 y = - 2 x + 2,

k ₁ =

Выпишем уравпепие параллельной прямой (используя задачу 29: y — yо = k (x

xо)):

y - 9 = - 2(x - 5).

August 31, 2013 Курбатов В.Г.

Выпишем уравнение иернендикулярной прямой (используя условие перпендикуляр­ности k 1 k 2 = - 1):

2 y-9 = - (x-5).

П

7.6 Кривые 2-го порядка, их общее уравнение

Уравнением 2-го порядка называют уравнение вида

a11x2 + 2a12xy + a 22 y 2 + 2 b 1 x + 2 b 2 y + c = 0.

Линию, задаваемую уравнением 2-го порядка, называют кривой 2-го порядка.

При замене координат уравнение может упрощаться. Путем поворота системы координат моясно добиться того, чтобы a 12 = 0, а путем сдвига, как правило, допол­нительно — чтобы b 1 = b 2 = 0. Получающееся уравнение называют каноническим.

Нормальным уравнением окружности называют уравнение

x

y ²

R ².

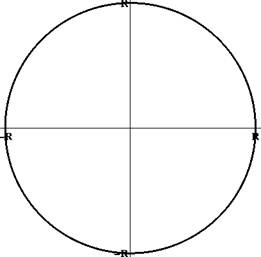
Оно задает окружность радиуса R с центром в начале координат. Сдвигая начало координат в точку (x ₀ ,y ₀ ), получаем уравнение

(x - x ₀ )2 + (y- y ₀)² = R ² .

Правило. Кривая F (x - x ₀ ,y - y ₀ ) = 0 получается из кривой F(x,y) сдвигом вправо на x ₀ и сдвигом вверх на y ₀-

Xy 0

Рис. 4: Окруж;ности

August 31, 2013 Курбатов В.Г.

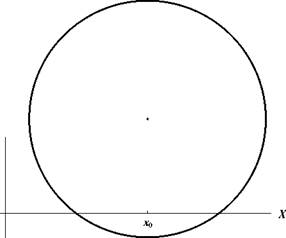
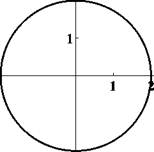
Задача 32. Изобразить кривую (x - 5)2 + (y + 3)2 = 4.

Решение. Это — окруясность, получающаяся из окружности x ² + y 2 = 4 путем
сдвига па вектор (5, - 3). Окружность x ² + y ² = 4 имеет радиус 2. П

Рис. 5: Окруж;ности

7.7 Выделение полного квадрата

Полным квадратом называют выраж;ение

поскольку его можно преобразовать к виду (a + b)2. Выделение полного квадрата — важная процедура при построении кривых второго порядка. Например, уравнение

ax ² + ay ² + 2bix + 2b2y + c = 0,

называемое общим уравнением окружности, всегда можно привести к виду

(x - x о)2 + (y - y о)2 = R ² .

Задача 33. Выделить полный квадрат в выраж;ении x 2 - 6 x + 5.

Решение. Имеем

x 2 - 6 x + 5 = x 2 - 2 x · 3 + 32 - 32 + 5

= (x 2 - 2 x · 3 + 32) - 4 = (x - 3)² - 4 .

Такое преобразование удобно, например, для построения графика функции y = x2

6 x + 5. -

Задача 34. Построить кривую x 2 - 10 x + y ² + 6 y + 30 = 0.

August 31, 2013 Курбатов В.Г.

Решение. Выделяем полные квадраты:

Получилось уравнение из задачи 32.

x ² - 10 x + y ² + 6 y + 30 = 0

x ² - 2 x · 5 + y ² + 2 y · 3 + 30 = 0

x ² - 2 x · 5 + 5² - 5² + y ² + 2 y · 3 + 3² - 3² + 30 = 0

(x ² - 2 x · 5 + 5²) + (y ² + 2 y · 3 + 3²) + 30 - 5² - 3² = 0

(x - 5)² + (y + 3)² - 4 = 0.

7.8 Эллипс

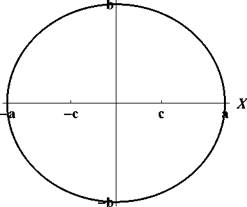
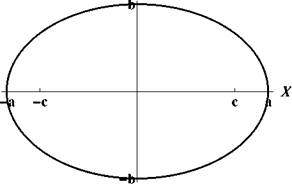
Эллипсом называют кривую, заданную уравнением

x ² y ²

+ a ² b ²

1.

А само уравнение называют каноническим уравнением эллипса. Числа a иb называ­ют полуосями, а точки пересечения с осями — вершинами.

Точки с координатами (c, 0) и (— c, 0), где c = ^a"^ — b ^, называют фокусами.

Рис. 6: Эллипсы

Задача 35. Определить вид и расположение кривой x^ — 6x + 4y^ — 16y + 21 приведя ее уравнение к каноническому виду.

= 0,

August 31, 2013 Курбатов В.Г.

Решение. Выделяем полные квадраты:

х ² -6х + 4 ² - 16у + 21 = 0

ж² - 2ж · 3 + 4(у2 - 2 · у · 2) + 21 = 0

ж2 - 2ж · 3 + 32 - 32 + 4(у2 - 2 · у · 2 + 22 - 22) + 21 = 0

(х2 -2х·3 + 32) + 4(у2 - 2 · у · 2 + 22) + 21 - 32 - 4 · 22 = 0

(ж - 3)2 + 4(у - 2)2 - 4 = 0

22 12

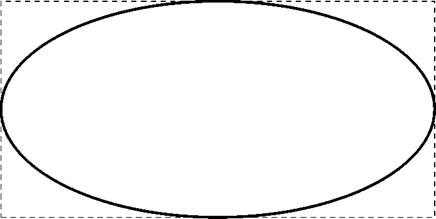
Получился эллипс с центром в точке (3,2) и полуосями 2 и 1. В качестве вспомо­гательного построения сначала рисуем прямоугольник с нужными полуосями. П

Рис. 7: Эллине из задачи 35

7.9 Гипербола

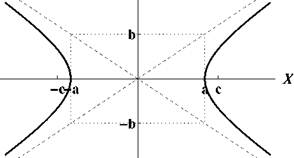
Гиперболой называют кривую, заданную уравнением

x

y ² b ²

1.

August 31, 2013 Курбатов В.Г.

Само уравнение называют каноническим уравнением гиперболы. Числа a и b на­зывают полуосями, а точки пересечения с осями — вершинами. Прямые y = ± - x называют асимптотами гиперболы. Если a = b гиперболу называют равносторон­ней. Точки с координатами (c, 0) и (— c, 0), где c = ya? + b, называют фокусами.

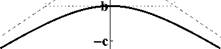
Рис. 8: Гиперболы с уравнениями ^

62

62

= 1

Правило рисования: Сначала рисуют прямоугольник с полуосями a и b, затем через его вершины проводят асимптоты, а затем — саму гиперболу.

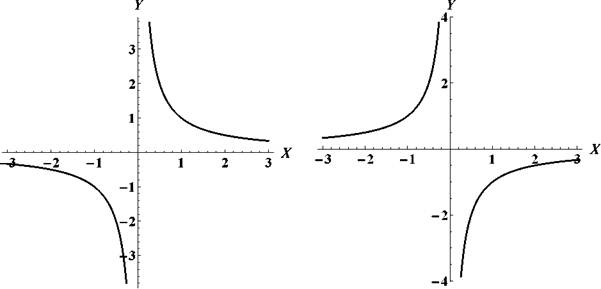
Рис. 9: Гиперболы y = - -а y = —-

Кривая y = - является равносторонней гиперболой, повернутой но отношению к канонической на угол 45°.

August 31, 2013 Курбатов В.Г.

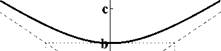
7.10 Парабола

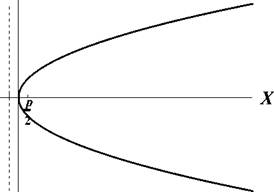
Параболой называют кривую, заданную уравнением

y ² = 2 px.

Само уравнение называют каноническим уравнением параболы. Число p называют параметром параболы, а точку (0,0) — вершиной. Точку с координатами (^p ₂,0) на­зывают фокусом, а прямую x = - ^p ₂ — директрисой.

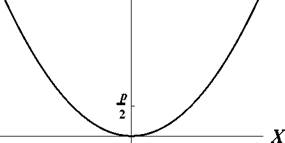
Рис. 10: Параболы y2 = 2px и 2 py = x 2

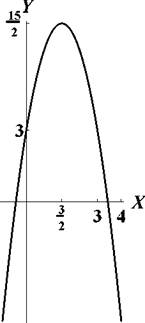
Задача 36. Построить кривую y = - 2 x 2 + 6 x + 3. Решение. Выделим полный квадрат:

y = - 2 x 2 + 6 x + 3,

	y = - 2(x 2 - 3 x) + 3,
y =	/ 2 332 32
y =	x 2 3 32\ 9
	2/ 3\ 15
	15 / 3\ y- 2 = - 2 x- 2) .

Птак, получилась парабола y

2 x ², верп1ина которой смещена в точку |, ₂

7.11 Уравнение плоскости

Общим уравнением плоскости называют уравнение вида

Ax + By + Cz + D = 0

August 31, 2013 Курбатов В.Г.

Рис. 11: Парабола из задачи 36

в предполоясении, что хотя бы один из коэффитщеитов A, B или C отличен от нуля. Покажем, что вектор n ¯ = (A, B, C) является перпендикулярным плоскости. Вектор n ¯ = (A, B, C) называют нормальным от слова "нормаль" вектором плоскости. Пусть точка Mo(xo,yo,zo) принадлежит плоскости, т. е.

Axо + Byо + Czo + D = 0.

Вычитая предыдущие равенства друг из друга, приходим к уравнению

A (x - xо) + B (y - yо) + C(z - zo) = 0,

(7.3)

которое можно интерпретировать как равенство нулю скалярного произведения век­торов n ¯ = (A, B, C) и MqM = (x - x о,y - yo,z - z q). Таким образом, уравнению удовлетворяют в точности те точки M, для которых вектор MqM нернендикулярен вектору n ¯.

Задача 37. Составить уравнение плоскости, проходящей через точку (5,7 ,- 3) пер­пендикулярно вектору (4 ,- 6,8).

Решение. Уравнение (7.3) является решением задачи: составить уравнение плос­кости, проходящей через точку (xo,yo,zo) перпендикулярно вектору (A, B, C). Оста­ется подставить нап1и данные:

4(x - 5) - 6(y - 7) + 8(z + 3) = 0. Далее мож;но раскрыть скобки и привести подобные.

Если хотя бы один из коэффициентов A, B или C равен нулю, то уравнение плос­кости называют неполным. Например, если C = 0, то вектор n ¯ = (A, B, 0) параллелен плоскости XY, и значит, сама прямая параллельна оси Z.

August 31, 2013 Курбатов В.Г. 60

August 31, 2013 Курбатов В.Г. 61

и условие перпендикулярности

A1·A2 + B1·B2 + C1·C2 = 0 двух плоскостей.

7.12 Уравнение прямой

Прямую в пространстве можно задать как пересечение двух плоскостей, т. е. как множество решений системы уравнений

A1x + B1y + C1z + D1 = 0, A2x + B2y + C2z + D2 = 0.

Эти две плоскости определены неоднозначно. Разумно выбирать их возмож;но более простыми. Считается, что самый простой вид — это

x - x 1	y - y 1	z - z 1
l	m	n

(7.4)

Здесь два уравнения. Например, уравнение

x - x1 = y - y ₁
l m

задает плоскость, параллельную оси Z.

Уравнения (7.4) называют каноническими уравнениями прямой.

Очевидно, точка (x 1 ,y ₁ ,z ₁) леж;ит на прямой. Вектор q = (l,m,n) параллелен прямой. Его называют направляющим вектором прямой.

Задача 39. Составить уравнение прямой, проходящей через точку (5,7 ,- 3) парал­лельно вектору (4, - 6, 8).

Решение. Уравнение (7.4) является решением задачи: составить уравнение пря­мой, проходящей через точку (x1,y1,z ₁ ) параллельно вектору (l,m,n). Остается под­ставить наши данные:

x - 5 y - 7 z + 3

4 - 6 = 8

Углы между плоскостями и прямыми — это по определению углы меж;ду их нор­мальными и направляющими векторами. Их находят с помощью теоремы 17. В част­ности, имеем условие параллельности

1 1 m ₁ n ₁

и условие перпендикулярности

l ₁ · l2 + m ₁ · m2 + n ₁ · n2 = 0

двух прямых.