Установившийся режим
Неустановившийся режим
При φ > 1 установившегося режима не существует, т.е. заявки прибывают, очередь растет неограниченно, так как средний интервал между обслуживаниями отдельных заявок 1/λ(t) больше среднего интервала 1/μ(t) между поступающими заявками.
При φ < 1 поток также не устанавливается, но в этом случае 1/λ(t) меньше 1/μ(t), т.е. очередь убывает, что может привести к окончанию потока заявок и к простою каналов обслуживания.
Поток устанавливается при φ = 1. При установившемся режиме очередь постоянна. Установившийся режим не зависит от начальных условий.
Наилучшим примером решения задач по моделям систем массового обслуживания является создание вычислительных систем, управляемых операционными системами строго в соответствии с детерминированными законами очереди и обслуживания заданий (решаемых задач).
Наибольшей сложностью моделей характеризуются многопроцессорные комплексы или сети вычислительных систем. Хуже всего реализуется организация социально-экономических систем из-за сложности формализации законов их функционирования.
|
|
|
Под вероятностью системы понимается отношение числа совершившихся событий к общему числу возможных событий:
P = ncc / n,
где n сс – число совершившихся событий; n – общее число событий.
Вероятность поступления заявок в очередь в момент времени t определяется по формуле
Р вх(t) = λ(t) dt.
Вероятность обслуживания заявок в очереди, в момент времени t определяется по формуле
Р вых(t) = μ(t) dt.
Рассмотрим ряд состояний, в которых может находиться система массового обслуживания:
Состояние Е 0
1. Заявок нет.
 |
Состояние Е 1
2. Одна заявка обслуживается.
 |
Состояние Е2.
3. Одна заявка обслуживается и одна стоит в очереди.
 |
Состояние Е n
4. Одна заявка обслуживается и n –1 заявок стоит в очереди
(V = n -1).
 |
Средняя стоимость обслуживания в СМО в единицу времени: 
Y = VC 1 + ρ C 2,
где C 1 – стоимость ожидания одной заявки в единицу времени; V – среднее число заявок в очереди; C 2 – стоимость работы канала обслуживания в единицу времени; ρ – среднее число каналов обслуживания.
Для определения дифференциальных уравнений состояний системы массового обслуживания обозначим через J стохастическую матрицу (матрицу переходов системы из одного состояния в другое), а через Р стохастический вектор. Вероятность обозначается Рn 1 n, где n 1 – предыдущее состояние системы; n – последующее состояние системы; Р 01 = λd t обозначает вероятность возникновения в системе одной заявки.
Переходы системы из одного состояния в другое можно описать следующими уравнениями:
|
|
|
| Изменение состояния: | Вероятность перехода: |
| Е 0 → Е 1 | Р 01 = λ(t)d t, n =1 |
| Е 0 → Е 0 | Р 00 = 1 – λ(t)d t |
| Е 0 → Е 2 | Р 02 = 0 |
| Е 0 → Еn | Р 0n = 0, n ≥ 2 |
| Е 1 → Е 0 | Р 10 = μ(t)d t |
| Е 1 → Е 2 | Р 12 = λ(t)d t |
| Е 1 → Е 1 | Р 11 = 1 – (λ(t) + μ(t))d t |
В общем виде это можно выразить следующей системой уравнений:
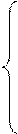 Р 00 = 1 – λ(t)d t Р 00 = 1 – λ(t)d t
|
| Рi, i +1 = λ(t)d t |
| Рi, i = 1 – (λ(t) + μ(t))d t |
| Рi –1, i = μ(t)d t |
Составим стохастическую матрицу переходов из одного состояния в другое
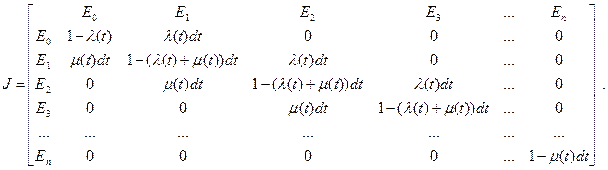
Сумма элементов стохастической матрицы в одной строке равна единице:
Р i0 + Р i1 + Р i2 +... Р in = μ(t)dt + [1–(λ(t)+μ(t))dt] + λ(t)dt = 1
Вектор состояния системы отражает вероятность возникновения перехода 0 → n.
Стохастический вектор:

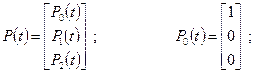
Тогда:
Р (t)/ Р (t + dt) = Р (t) *J – рекуррентная функция;
Р (dt) = Р (0) *J – вероятность возникновения состояния через промежуток времени dt.
В общем виде это можно выразить следующей системой уравнений:
 Р 0(t+dt) = (1 – λ (t) dt) Р 0(t) + μ(t) dt Р 1(t)
Р 0(t+dt) = (1 – λ (t) dt) Р 0(t) + μ(t) dt Р 1(t)
Р 1 (t+dt) = λ(t)dt Р 0 (t) + [1 – (μ(t) + λ(t)) dt ] Р 1(t) + μ(t) dt Р 2(t)
Рi (t+dt) = λ(t) dt Рi- 1(t) + [1 – (μ(t) + λ(t)) dt ] Рi (t) + μ(t) dt Рi+ 1(t)
при i ≥ 1.
Данные соотношения можно пояснить так. Событие Еn в момент t+dt может быть реализовано одним из трех способов:
1. в момент t в системе была (n – 1) заявка, а в интервале dt поступила одна заявка;
2. в момент t в системе было n заявок, а за время dt ни одна заявка не поступила и обслуживание очередной заявки не окончилось;
3. в момент t в системе была (n + 1) заявка, а за время dt одна из заявок была обслужена.
Произведя соответствующие преобразования, получим:
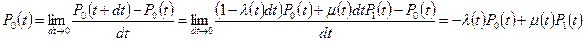

при i ≥ 1.
Таким образом, система уравнений состояний системы массового обслуживания имеет вид:
 Р 0(t) = – λ(t) Р 0(t) + μ(t) Р 1(t)
Р 0(t) = – λ(t) Р 0(t) + μ(t) Р 1(t)
Рi(t) = λ (t) Рi- 1(t) – (λ(t) + μ(t)) Рi (t) + μ(t) Рi+ 1(t).
 2014-02-09
2014-02-09 853
853








