Определение. Система истинностных функций называется полной, если с помощью функций этой системы можно выразить любую истинностную функцию

Полные системы истинностных функций

Теорема. Всякая истинностная функция, не равная тождественно Л, может быть представлена в СДНФ. Всякая истинностная функция, не равная тождественно И, может быть представлена в СКНФ.

Определение. Конъюнкция, составленная из элементарных дизъюнкций, называется совершенной конъюнктивной нормальной формой (СКНФ).

Определение. Дизъюнкция, составленная из элементарных конъюнкций, называется совершенной дизъюнктивной нормальной формой (СДНФ).

Составленная СДНФ выражает ту же истинностную функцию, что и истинностная таблица.

□ Пусть при данном наборе (P₁,..., Р_п) истинностная функция, согласно истинностной таблице, имеет значение И: f(P₁,..., Р_п)= И. Тогда этот набор будет среди выбранных, значит, среди составленных элементарных конъюнкций будет такая, которая при данном наборе примет значение И. Поэтому в СДНФ будет один (и только один) член, имеющий значение И. По определению дизъюнкции значение И будет иметь и СДНФ.

Пусть теперь при данном наборе (P₁,..., Р_п) истинностная функция, согласно истинностной таблице, имеет значение JI. Тогда этого набора не будет среди выбран­ных, и, значит, все составленные элементарные конъюнк­ции будут иметь значение Л (элементарная конъюнкция обладает свойством принимать значение И только при том наборе, для которого она составлена). Итак, все члены СДНФ, а поэтому и она сама имеют значение JI. ■

Алгоритм СКНФ (совершенная конзъюнктивная нормальная форма). Этот алгоритм аналогичен алгоритму СДНФ.

1. Выбираем все те наборы значений атомов P₁,..., Р_п, при которых истинностная функция имеет значение Л.

И	Л	Л
Л	И	Л
Л	Л	И
Л	Л	Л

2. Для каждого из этих наборов составляем дизъюнкцию из атомов P₁,..., Р_п или их отрицаний, такую, что при данном наборе она принимает значение Л.

¬ P₁ Ú P₂ Ú P_з.

P₁ Ú¬ P₂ Ú P_з.

P₁ Ú P₂ Ú¬ P_з.

P₁ Ú P₂ Ú P_з.

Дизъюнкции, содержащие все п атомов P₁,..., Р_п (с отрицаниями или без них), называются элементарными дизъюнкциями (длины п).

3. Составляем конъюнкцию выписанных элементарных дизъюнкций.

(¬ P₁ Ú P₂ Ú P_з)Ù(P₁ Ú¬ P₂ Ú P_з)Ù(P₁ Ú P₂ Ú¬ P_з)Ù(P₁ Ú P₂ Ú P_з).

Составленная СКНФ выражает ту же истинностную функцию, что и истинностная таблица.

Из теоремы следует, что для выражения любой истинностной функции достаточно трех логических операций: отрицания, конъюнкции и дизъюнкции.

Система { ^Ø, Ù. Ú} — полная, что следует из предыдущей теоремы.

Существуют и более “бедные” функциями системы, являющиеся полными. Теорема. Системы истинностных функций

{^Ø, Ù }, {^Ø, Ú }, {^Ø, Þ}– полные .

□ Для доказательства полноты системы { ^Ø, Ù} достаточно, исходя из полноты системы { ^Ø, Ù. Ú} выразить дизъюнкцию через отрицание и конъюнкцию. Но это имеет место в силу равносильности

А Ú В ≡ ^Ø (^Ø А Ù ^Ø В). (1)

Полнота системы { ^Ø, Ú} следует из равносильности

А Ù В ≡^Ø (^Ø А Ú ^Ø В). (2)

Полнота системы { ^Ø, Þ } следует из равносильности

А Þ В ≡ ^Ø А Ú В. (3)

Равносильности (1), (2), (3) можно доказать, например, составлением истинностных таблиц. ■

Среди указанных в таблице двухместных истинностных функций имеются и такие, которые в единственном числе образуют полную систему истинностных функций.

Например, функции штрих Шеффера (отрицание конъюнкции или дизъюнкция отрицаний 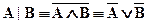) и стрелка Пирса (отрицание дизъюнкции или конъюнкция отрицаний ):

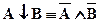А	В	А| В		А	В	А¯В
И	И	Л		И	И	Л
И	Л	И		И	Л	Л
Л	И	И		Л	И	Л
Л	Л	И		Л	Л	И

Теорема. Системы истинностных функций {|} и {¯} – полные .

□ Полноту системы {|} доказывают равносильности:

^ØА º А | А,

АÚВ= (А | А) | (В | В)

АÙВ= (А | В) | (А | В)

Покажем, что Ø и Ù выражаются через |.

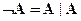
А	А|A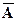
и	л	л
л	и	и

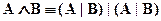
А	В	А|В	(А|B)|(A|B)	AÙB
и	и	л	и	и
и	л	и	л	л
л	и	и	л	л
л	л	и	л	л

Т.к. 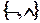- полная система функций, а {|} выражается через 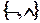, то{|} - полная система.

Полноту системы {¯} доказывают равносильности:

^ØА º А¯А,

АÙВ= (А¯А)¯(В¯В)

АÚВ= (А¯В)¯(А¯В)

Выразим 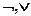через ¯

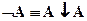
A		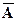A¯A
и	л	л
л	и	и

Покажем, что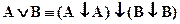

А	В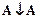
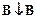
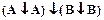
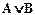
и	и	л	л	и	и
и	л	л	и	л	л
л	и	и	л	л	л
л	л	и	и	л	л

Т.к. {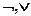}- полная система функций, то 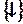- полная система функций. ■