Поэтому резонансное сопротивление становится равным

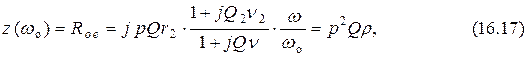
что меньше аналогичного сопротивления простого контура с теми же значениям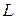и и .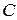

Зависимость модуля сопротивления сложного параллельного колебательного контура с двумя индуктивностями с учётом потерь приведена на рис. 16.9.

Сложный контур применяют, если резонансное сопротивление простого контура больше требуемого. Подбирая коэффициент включения, можно уменьшить 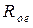, не ухудшая добротность контура. Кроме того, если требуется, то последовательный резонанс в ветви удобно использовать для подавления сигналов вблизи частоты .

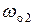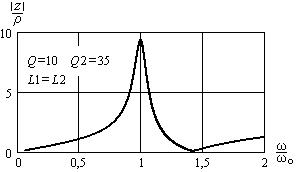
Рис. 16.9. Частотная характеристика сопротивления сложного параллельного контура с двумя индуктивностями с учётом потерь

16.4. Параллельный колебательный контур с двумя емкостями*

Параллельный колебательный контур с двумя емкостями также называют сложным (рис. 16.1, в).

Найдём сопротивления ветвей для контура без потерь:

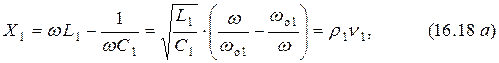
и

где 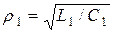– характеристическое сопротивление, 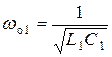– резонансная частота левой ветви контура, 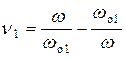– относительная расстройка левой ветви контура.

Используя формулу (16.2), получаем выражение входного сопротивления идеального (без потерь) сложного параллельного колебательного контура с двумя емкостями

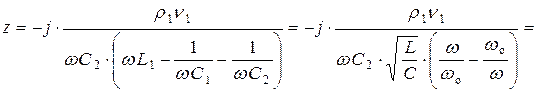
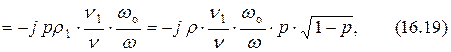
где 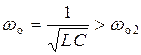– резонансная частота контура, 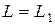– индуктивность, 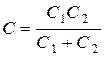– полная ёмкость.

Согласно определению коэффициент включения равен

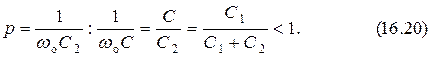
Приняв частоту 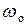в качестве базовой, выразим через неё резонансную частоту и относительную расстройку левой ветви

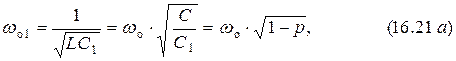
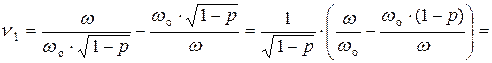
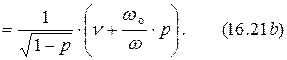
Использование формулы 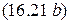в выражении (16.19) упрощает расчёты.

Зависимости сопротивления (16.19) от частоты приведены на рис. 16.10.

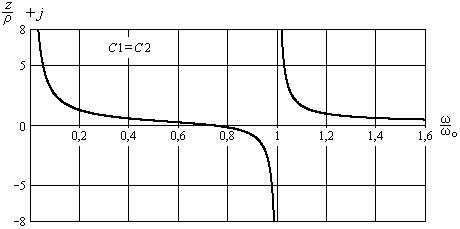
Рис. 16.10. Частотная зависимость сопротивления идеального параллельного колебательного контура с двумя емкостями

Потерями правой ветви контура можно пренебречь на частотах выше той, с которой начинает выполняться условие 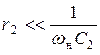. Как правило, 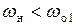. Потерями левой ветви пренебрегать нельзя, так как на резонансе этой ветви её реактивное сопротивление становится равным нулю. Также нельзя пренебрегать потерями обеих ветвей вблизи резонансной частоты контура 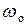, когда реактивная составляющая в знаменателе сопротивления контура становится равной нулю.

С учётом сказанного сопротивление (16.1) для сложного контура может быть записано в виде

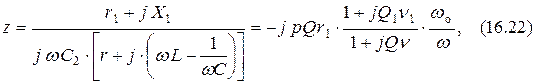
где 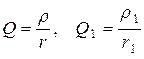– добротности всего контура и левой ветви соответственно.

На резонансной частоте 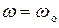имеют место соотношения 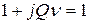и 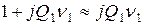. Поэтому резонансное сопротивление становится равным

что меньше аналогичного сопротивления простого контура с теми же значениям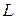и и .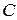

Зависимость модуля сопротивления параллельного колебательного контура с двумя емкостями приведена на рис. 16.11.

Как и в случае контура с двумя индуктивностями сложный контур применяют, если резонансное сопротивление простого контура больше требуемого. Подбирая коэффициент включения, можно уменьшить 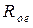, не ухудшая добротность контура. Кроме того, если требуется, то последовательный резонанс в ветви удобно использовать для подавления сигналов вблизи частоты .

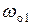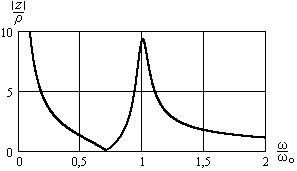
Рис. 16.11. Частотная характеристика сопротивления сложного параллельного колебательного контура с двумя емкостями с учётом потерь

* Данный раздел студенты изучают самостоятельно