Пример 1. Линейная оптимизационная модель годовой производственной программы предприятия.
Производственная мощность предприятия характеризуется величиной годового максимально – возможного выпуска продукции при применении прогрессивных технологий, эффективной организации производства и наиболее полном использовании производственного оборудования предприятия. Математическая модель для определения производственной программы должна иметь критерий эффективности со стоимостными показателями продукции, хотя они имеют ряд недостатков (изменение цен на продукцию из-за инфляционных процессов, ставок оплаты труда, цен на сырье и др.)
Для построения модели введем обозначения:
· 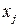 - объем производства продукции
- объем производства продукции 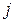 - го вида,
- го вида, 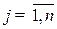 ;
;
· 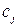 - стоимость единицы продукции
- стоимость единицы продукции 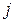 - го вида,
- го вида, 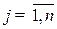 ;
;
· 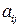 - время обработки
- время обработки 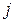 - ой продукции на
- ой продукции на 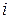 - том оборудовании;
- том оборудовании;
· 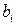 - фонд времени работы оборудования
- фонд времени работы оборудования 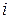 - го вида.
- го вида.
Математическая модель рассматриваемой задачи будет иметь вид:
Найти план 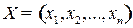 выпуска продукции, при котором предприятие получит максимум выручки
выпуска продукции, при котором предприятие получит максимум выручки
|
|
|
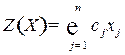
при ограничениях на фонд времени работы оборудования
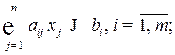
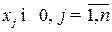 .
.
Частным случаем рассматриваемой модели является оптимизационная модель использования ресурсов.
Предположим, что предприятие может изготавливать четыре вида продукции 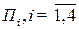 . Предприятие располагает ресурсами и нормами их расхода, приведенными в таблице 1.1
. Предприятие располагает ресурсами и нормами их расхода, приведенными в таблице 1.1
Таблица 1.1
| Ресурсы | Продукция | Объем ресурса | |||
| П-1 | П-2 | П-3 | П-4 | ||
| Трудовые ресурсы, человеко-смены | 2,5 | 2,5 | 1,5 | ||
| Полуфабрикаты, кг | |||||
| Станочное оборудование, станко-смены | |||||
| Прибыль от единицы продукции, ден. ед. |
Требуется: 1) определить план выпуска продукции, максимизирующей прибыль предприятия;
2) учесть требование комплектации, чтобы количество единиц третьей продукции было в два раза больше количества единиц первой;
3) определить оптимальный ассортимент при дополнительных условиях: первой продукции выпускать не менее 27 единиц, третьей – не более 35, а второй и четвертой – в отношении 2:3.
Построим математическую модель задачи. Для этого введем неизвестные величины 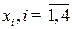 , характеризующие количество произведенной продукции. Критерий оптимальности – стоимостной (максимум прибыли предприятия). Следовательно, нужно определить план выпуска продукции
, характеризующие количество произведенной продукции. Критерий оптимальности – стоимостной (максимум прибыли предприятия). Следовательно, нужно определить план выпуска продукции 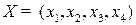 , при котором целевая функция
, при котором целевая функция 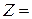
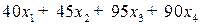 достигает максимального значения и который удовлетворяет системе ограничений:
достигает максимального значения и который удовлетворяет системе ограничений:
· на трудовые ресурсы: 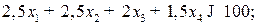
· на полуфабрикаты: 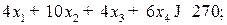
· на станочное оборудование: 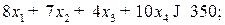
· условию неотрицательности переменных: 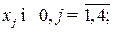
· дополнительное требование комплектации: 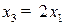 ;
;
|
|
|
· дополнительные условия: 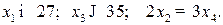
Линейная оптимизационная модель построена. Способы решения рассмотрим ниже.
Пример 2. Линейная оптимизационная модель о выборе технологий.
Предположим, что для выпуска некоторой однородной продукции можно использовать 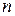 технологий и при этом используются
технологий и при этом используются 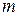 видов ресурсов, заданных соответственно объемами
видов ресурсов, заданных соответственно объемами 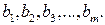
Построим математическую модель, решая которую определим оптимальную технологию для выпуска однородной продукции. Пусть: 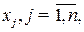 - время, в течение которого предприятие выпускает продукцию по
- время, в течение которого предприятие выпускает продукцию по 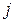 - тому технологическому способу;
- тому технологическому способу;
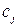 ,
,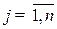 , - стоимость конечной продукции, производимой в единицу времени, по
, - стоимость конечной продукции, производимой в единицу времени, по 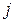 - тому технологическому способу;
- тому технологическому способу;
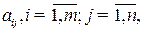 - расход
- расход 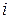 - го ресурса в единицу времени по
- го ресурса в единицу времени по 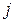 - тому технологическому способу.
- тому технологическому способу.
Пренебрегая временем переналадок, необходимым для перехода от одного технологического способа к другому, и воспользовавшись стоимостным критерием оптимальности, получим следующую математическую модель рассматриваемой задачи.
Определить оптимальное применение технологических способов 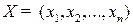 , при которых максимизируется объем выпуска (в ден. ед.) продукции:
, при которых максимизируется объем выпуска (в ден. ед.) продукции: 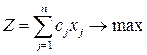
и, которые удовлетворяют системе ограничений:
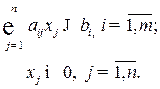
Предположим, что предприятие может работать по трем технологическим способам. Расход ресурсов за единицу времени при соответствующей технологии и производительность по каждому технологическому способу (в ден. ед.) в единицу времени, представим в таблице 1.2.
Таблица 1.2
| Ресурсы | Технологические способы | Объем ресурса | ||
| Т-1 | Т-2 | Т-3 | ||
| Трудовые ресурсы, человеко - часов | 1 300 | |||
| Сырье, т | ||||
| Электроэнергия, кВт/ч | 3 000 | |||
| Производительность технологического способа |
Определить план использования технологических способов, при котором максимизируется объем выпуска продукции.
Построим математическую модель задачи. Пусть 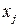 - время использования
- время использования 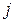 - го технологического способа. Требуется найти план
- го технологического способа. Требуется найти план 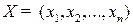 , при котором целевая функция
, при котором целевая функция
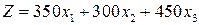
достигает максимального значения, и, который удовлетворяет ограничениям:
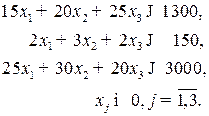
Пример 3.Линейная оптимизационная модель раскроя материалов.
На деревообрабатывающем предприятии листы фанеры для изготовления деталей изделий могут раскраиваться несколькими способами. Если лист раскроить по j -му способу раскроя (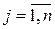 ), то получится
), то получится 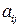 деталей i -го вида (
деталей i -го вида (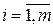 ), при этом отходы с одного листа равны
), при этом отходы с одного листа равны 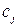 м2. Требуется найти, сколько листов фанеры раскраивать по каждому из способов раскроя, чтобы получить деталей i -го вида не менее
м2. Требуется найти, сколько листов фанеры раскраивать по каждому из способов раскроя, чтобы получить деталей i -го вида не менее 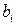 единиц, а количество отходов должно быть минимальным.
единиц, а количество отходов должно быть минимальным.
Составим математическую модель данной задачи.
Обозначим 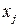 количество листов фанеры, раскраиваемых по j - тому способу. Определим план
количество листов фанеры, раскраиваемых по j - тому способу. Определим план 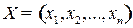 раскроя листов фанеры так, чтобы суммарное количество отходов по всем вариантам раскроя было минимальным:
раскроя листов фанеры так, чтобы суммарное количество отходов по всем вариантам раскроя было минимальным:
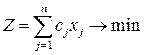
и чтобы выполнялись ограничения на изготовление деталей:
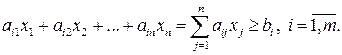
Количество листов фанеры, раскраиваемых по j - тому способу, должно быть неотрицательным:
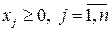 .
.
Пример 4. Линейная оптимизационная модель о рационе.
Сельскохозяйственное предприятие для откорма скота располагает n видами кормов (сочные, грубые, концентрированные и др.). Каждый вид корма характеризуется содержанием питательных веществ (кормовые единицы, белки, фосфор, кальций и др.). Известно содержание i -го питательного вещества в единице корма j -го вида и равно оно 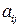 единиц (
единиц (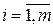 ,
, 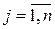 ), а также
), а также 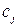 – стоимость единицы корма j -го вида (
– стоимость единицы корма j -го вида (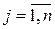 ) и минимальная суточная потребность скота в i -м питательном веществе
) и минимальная суточная потребность скота в i -м питательном веществе 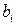 (
(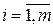 ). Требуется составить рацион минимальной стоимости.
). Требуется составить рацион минимальной стоимости.
Для построения математической модели данной задачи обозначим 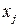 - количество корма
- количество корма 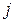 - го вида. Определим рацион
- го вида. Определим рацион 
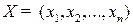 , при котором суммарная стоимость рациона:
, при котором суммарная стоимость рациона:
|
|
|
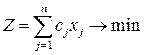
будет минимальной, а суточная потребность животного в питательном веществе 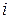 - го вида будет не менее минимального количества
- го вида будет не менее минимального количества 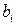 :
:
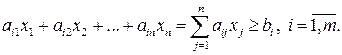
Количество корма, потребляемого животным, не может быть отрицательной величиной:
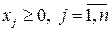 .
.
Пример 5. Линейная оптимизационная модель о назначениях.
Имеется n механизмов, которые могут использоваться для выполнения n работ. Известна производительность 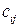 каждого i -го механизма (
каждого i -го механизма (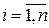 ). Требуется так закрепить механизмы за работами, чтобы суммарная их производительность была максимальной.
). Требуется так закрепить механизмы за работами, чтобы суммарная их производительность была максимальной.
Для составления математической модели задачи введем переменные:
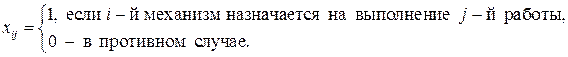
Найдем план использования механизмов так, чтобы их суммарная производительность была максимальной:
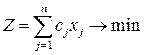 ,
,
при ограничениях:
· 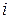 - ый механизм должен быть назначен только на одну работу:
- ый механизм должен быть назначен только на одну работу:
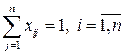 ,
,
· каждая работа должна выполняться только одним механизмом:
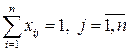 .
.
Пример 6. Линейная оптимизационная модель о размещениях.
Отраслью заключены договоры на поставку продукции потребителям в заданных ассортименте, объеме и сроках. Для выполнения договорных обязательств руководство отрасли разрабатывает мероприятия по расширению производства на ряде предприятий, проведению их реконструкции, а также строительству и вводу новых мощностей. Требуется определить объемы производства продукции на действующих, реконструируемых и вновь вводимых предприятиях, а также объемы поставок продукции от предприятий-поставщиков к потребителям, чтобы суммарные затраты на производство и доставку продукции были минимальными.
Введем обозначения и построим математическую модель задачи:
i – вид производимой продукции (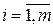 );
);
j – номер предприятия, производящего продукцию (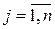 );
);
k – номер потребителя продукции (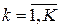 );
);
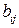 – мощности j -го предприятия по производству продукции i -го вида;
– мощности j -го предприятия по производству продукции i -го вида;
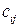 – стоимость производства единицы продукции i -го вида на j -м предприятии;
– стоимость производства единицы продукции i -го вида на j -м предприятии;
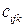 – затраты на перевозку единицы продукции i -го вида от j -го предприятия k -му потребителю;
– затраты на перевозку единицы продукции i -го вида от j -го предприятия k -му потребителю;
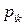 – объем поставки продукции i -го вида k -му потребителю согласно договорным обязательствам;
– объем поставки продукции i -го вида k -му потребителю согласно договорным обязательствам;
|
|
|
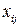 – искомый объем производства продукции i -го вида на k -м предприятии;
– искомый объем производства продукции i -го вида на k -м предприятии;
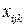 – объем поставки j -м предприятием продукции i -го вида k -му потребителю.
– объем поставки j -м предприятием продукции i -го вида k -му потребителю.
С учетом обозначений суммарные производственные и транспортные затраты в математической модели определяются следующим выражением
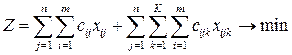 .
.
Ограничения задачи:
· по мощностям каждого предприятия
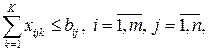
· по балансу производства и потребления продукции
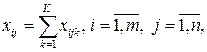
· по удовлетворению спроса потребителей
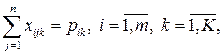
· объемы поставок и производства продукции должны быть неотрицательными:
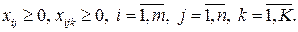
1.3. Графический способ решения линейных оптимизационных моделей. Рассмотрим линейнуюоптимизационную модель в общей форме записи:
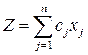 (1.8)
(1.8)
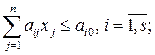 (1.9)
(1.9)
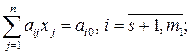 (1.10)
(1.10)
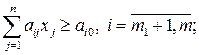 (1.11)
(1.11)
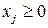 ,
, 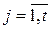 ; (1.12)
; (1.12)
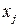 – произвольные,
– произвольные, 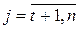 .
.
с геометрической точки зрения. Целевая функция (1.8) определяет семейство параллельных гиперплоскостей уровня цели, каждой из которых соответствует определенное значение функции 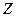 , так как при изменении
, так как при изменении 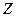 коэффициенты
коэффициенты 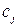 не меняются. Поскольку частные производные целевой функции по переменным
не меняются. Поскольку частные производные целевой функции по переменным 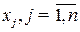 :
: 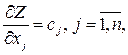 определяют координаты вектора
определяют координаты вектора 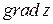 , то вектор
, то вектор 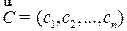 - это вектор градиентного направления и, следовательно, определяет направление наискорейшего возрастания целевой функции
- это вектор градиентного направления и, следовательно, определяет направление наискорейшего возрастания целевой функции 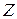 , а вектор
, а вектор 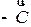 определяет направление наискорейшего убывания. Неравенства (1.9), (1.11) определяют полупространства, а (1.10) – гиперплоскости. Полупространства и гиперплоскости являются выпуклыми множествами. Множество точек выпукло, если отрезок, соединяющий две произвольные точки этого множества, принадлежит множеству. Пересечение конечного числа выпуклых множеств – множество выпукло. Следовательно, пересечение полупространств и гиперплоскостей определяет выпуклое множество, называемое многогранным множеством или многогранником. Многогранник (ограниченный или неограниченный) – это область допустимых решений
определяет направление наискорейшего убывания. Неравенства (1.9), (1.11) определяют полупространства, а (1.10) – гиперплоскости. Полупространства и гиперплоскости являются выпуклыми множествами. Множество точек выпукло, если отрезок, соединяющий две произвольные точки этого множества, принадлежит множеству. Пересечение конечного числа выпуклых множеств – множество выпукло. Следовательно, пересечение полупространств и гиперплоскостей определяет выпуклое множество, называемое многогранным множеством или многогранником. Многогранник (ограниченный или неограниченный) – это область допустимых решений  линейной оптимизационной модели. Особое значение имеют угловые (или крайние) точки области допустимых решений. Угловой (крайней) точкой выпуклого множества называется точка, если она не является внутренней ни для какого отрезка целиком принадлежащего множеству.
линейной оптимизационной модели. Особое значение имеют угловые (или крайние) точки области допустимых решений. Угловой (крайней) точкой выпуклого множества называется точка, если она не является внутренней ни для какого отрезка целиком принадлежащего множеству.
Так как планы линейнойоптимизационной модели – это упорядоченные совокупности n чисел (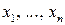 ), то их можно рассматривать как точки n ‑мерного пространства. Они образуют выпуклое множество, т. е. справедлива теорема:
), то их можно рассматривать как точки n ‑мерного пространства. Они образуют выпуклое множество, т. е. справедлива теорема:
Теорема. Множество планов линейнойоптимизационной модели является выпуклым.
Доказательство (для канонической линейнойоптимизационной модели). Линейнуюоптимизационную модель можно записать и в матричном виде:
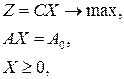
где 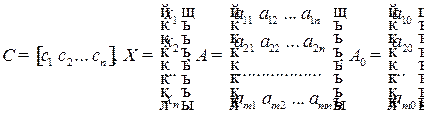 .
.
Пусть 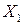 и
и 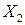 – планы канонической линейнойоптимизационной модели. Следовательно, они удовлетворяют системе ограничений:
– планы канонической линейнойоптимизационной модели. Следовательно, они удовлетворяют системе ограничений: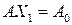 и
и 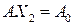 . Покажем, что линейная выпуклая комбинация планов
. Покажем, что линейная выпуклая комбинация планов 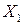 и
и 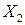
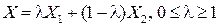
также является планом данной задачи. Действительно, подставив 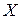 в систему ограничений, последовательно преобразовывая, получим верное равенство:
в систему ограничений, последовательно преобразовывая, получим верное равенство:
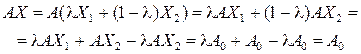
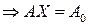
что и требовалось доказать.
Введением дополнительного неравенства:
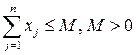 (достаточно большое)
(достаточно большое)
задачу с неограниченной областью планов формально можно преобразовать в задачу с ограниченной областью.
Поэтому в дальнейшем будем предполагать, что множество планов линейнойоптимизационной модели является выпуклым многогранником и называть его многогранником планов.
Таким образом, линейнуюоптимизационную модель на геометрическом языке можно сформулировать следующим образом: найти точку 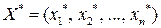 многогранника планов, определяемого системой ограничений (2.2) – (2.5), через которую проходит гиперплоскость семейства (2.1), соответствующая наибольшему (наименьшему) значению функции
многогранника планов, определяемого системой ограничений (2.2) – (2.5), через которую проходит гиперплоскость семейства (2.1), соответствующая наибольшему (наименьшему) значению функции 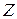 .
.
Пусть 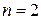 , тогда линейнаяоптимизационная модель на геометрическом языке формулируется следующим образом: найти точку
, тогда линейнаяоптимизационная модель на геометрическом языке формулируется следующим образом: найти точку 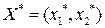 многоугольника (многоугольной области) планов, определяемого системой ограничений:
многоугольника (многоугольной области) планов, определяемого системой ограничений:
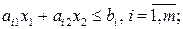 (1.13)
(1.13)
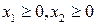 ,
,
через которую проходит прямая семейства
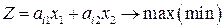 , (1.14)
, (1.14)
соответствующая наибольшему (наименьшему) значению функции 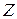 .
.
Прямые 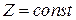 называются линиями уровня. Используя данную геометрическую интерпретацию, линейнуюоптимизационную модель (1.13)- (1.14) можно решить графически. Для этого:
называются линиями уровня. Используя данную геометрическую интерпретацию, линейнуюоптимизационную модель (1.13)- (1.14) можно решить графически. Для этого:
1) нужно построить многоугольник (многоугольную область) планов, т. е. множество допустимых решений Ω с учетом системы ограничений (1.13);
2) построить вектор 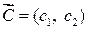 и одну из прямых семейства
и одну из прямых семейства 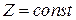 , например
, например 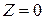 ;
;
3) параллельным перемещением прямой 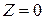 в направлении вектора
в направлении вектора 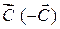 найти точку, в которой
найти точку, в которой 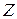 достигает максимума (минимума);
достигает максимума (минимума);
4) решая совместно уравнения прямых, пересекающихся в точке оптимума, найти ее координаты, а затем 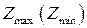 .
.
При определении оптимального плана возможны случаи:
1) функция 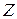 может достигать минимума в одной точке, а максимума – в любой точке отрезка;
может достигать минимума в одной точке, а максимума – в любой точке отрезка;
2) максимум может достигаться в одной точке, минимума не имеет (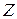 → –
→ –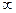 ) или минимум может достигаться в любой точке отрезка;
) или минимум может достигаться в любой точке отрезка;
3) функция 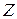 не имеет ни максимума (
не имеет ни максимума (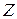 → +
→ +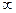 ), ни минимума (
), ни минимума (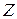 → –
→ –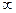 ).
).
Таким образом, оптимальный план может быть единственным; оптимальных планов может быть бесконечное множество; целевая функция может быть не ограничена; задача не имеет решения (см. рис. 1.1).

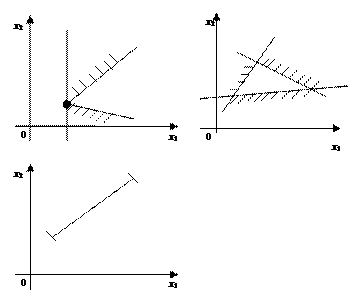
Рис. 1.1.
Анализируя рассмотренные случаи, можно сделать вывод: если целевая функция 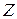 достигает оптимума, то это имеет место по крайне мере в одной из крайних точек области планов.
достигает оптимума, то это имеет место по крайне мере в одной из крайних точек области планов.
Отметим, что графическим методом можно решать линейнуюоптимизационную модель со многими переменными. Нужно, чтобы в канонической записи задачи разность между числом неизвестных (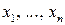 ) – n и числом линейно независимых уравнений r было равно двум: n – r = 2. Преобразовав такую задачу к симметричной форме, получаем линейнуюоптимизационную модель с двумя переменными, которую и решают графически. Найдя две координаты точки оптимума, подставляют их в ограничения. Решая полученную систему уравнений, определяем остальные координаты точки оптимума.
) – n и числом линейно независимых уравнений r было равно двум: n – r = 2. Преобразовав такую задачу к симметричной форме, получаем линейнуюоптимизационную модель с двумя переменными, которую и решают графически. Найдя две координаты точки оптимума, подставляют их в ограничения. Решая полученную систему уравнений, определяем остальные координаты точки оптимума.
Пример 1.1. Две базы поставляют продукцию трем потребителям. Объемы запасов, потребности и затраты на перевозку единицы продукции с баз представлены в таблице 1.3:
Таблица 1.3
| Базы | Потребители | Запасы | ||
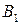
| 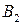
| 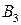
| ||
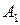
| ||||
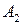
| ||||
| Потребности |
Необходимо спланировать перевозки таким образом, чтобы затраты на них были минимальными.
Решение. Обозначим через 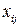 количество единиц продукции, которые нужно перевезти с базы
количество единиц продукции, которые нужно перевезти с базы 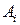 к потребителю
к потребителю 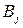 . Построим распределительную таблицу 1.4:
. Построим распределительную таблицу 1.4:
Таблица 1.4
| Базы | Потребители | Запасы | |||||
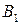
| 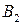
| 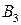
| |||||
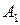
| 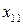
| 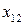
| 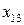
| ||||
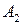
| 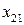
| 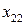
| 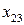
| ||||
| Потребности | min 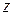
|
Составим математическую модель. Определим план перевозок таким образом, чтобы минимизировать стоимость перевозок:
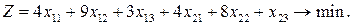
При этом должны выполняться следующие ограничения:
1) продукция с баз должна быть вывезена:
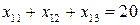 ;
;
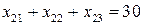 ;
;
2) заявки потребителей должны быть удовлетворены полностью:
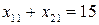 ;
;
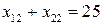 ;
;
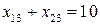 ;
;
1) должны быть исключены обратные перевозки:
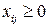 , i = 1, 2; j = 1, 2, 3.
, i = 1, 2; j = 1, 2, 3.
Это модель закрытой транспортной задачи. Так как
nm – (n + m – 1) = 2 · 3 – (2 + 3 – 1) = 2,
то задача может быть решена графически.
Выберем две свободные неизвестные, например, 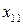 и
и 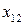 . Выразим все другие переменные через свободные, получим:
. Выразим все другие переменные через свободные, получим:
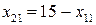 ;
; 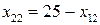 ;
; 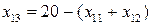 ;
;
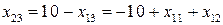 .
.
Подставим значения 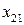 ,
, 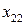 ,
, 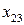 , выраженные через свободные переменные, в целевую функцию:
, выраженные через свободные переменные, в целевую функцию:
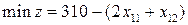 .
.
Из требования неотрицательности всех переменных (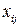 ≥ 0) имеем:
≥ 0) имеем:
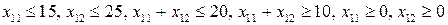 .
.
Целевая функция 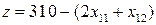 достигает минимума, если функция:
достигает минимума, если функция: 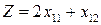 достигает максимума. Найдем
достигает максимума. Найдем 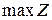 . Для этого выполним следующие действия:
. Для этого выполним следующие действия:
1) построим область Ω – множество допустимых решений, удовлетворяющих системе ограничений:
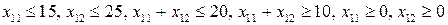 .
.
Для построения области 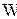 строим на плоскости
строим на плоскости 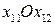 граничные прямые:
граничные прямые:
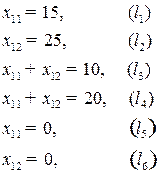
соответствующие данным неравенствам (см. рис. 1.2).


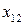


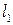
 |


 25
25 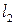

 20
20
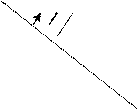







 10
10 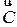
 | |||||
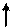 | |||||
 | |||||
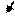

 0 10 15 20
0 10 15 20 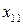
 |
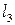
Рис. 1.2.
Каждая из них делит плоскость на две полуплоскости, одна из которых является решением соответствующего неравенства. Для выбора полуплоскости, являющейся решением неравенства, подставляем начало координат 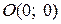 в каждое неравенство. Если получаем верное неравенство, то полуплоскость, содержащая начало координат, является решением неравенства, в противном случае – полуплоскость, не содержащая начало координат, является решением.
в каждое неравенство. Если получаем верное неравенство, то полуплоскость, содержащая начало координат, является решением неравенства, в противном случае – полуплоскость, не содержащая начало координат, является решением.
Стрелки указывают полуплоскости, являющиеся областями решений данных неравенств. Пересечение отмеченных полуплоскостей – заштрихованный многоугольник на рис. 1.2 – область решения данной системы.
2) построим вектор 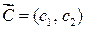 ,
, 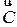 = (2, 1);
= (2, 1);
3) проведем линию 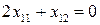 уровня цели перпендикулярно вектору
уровня цели перпендикулярно вектору 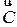 ;
;
4) так как ищется максимум 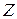 , то, прямую
, то, прямую 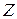 = 0, будем перемещать в направлении вектора
= 0, будем перемещать в направлении вектора 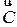 , так чтобы она заняла крайнее положение в области Ω;
, так чтобы она заняла крайнее положение в области Ω;
5) решаем систему из уравнений прямых, пересекающихся в точке оптимума:
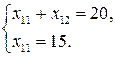
6) находим координаты точки оптимума:
 .
.
7) далее находим значения остальных неизвестных 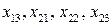 :
:
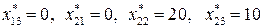 .
.
Тогда минимум целевой функции: 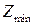 = 310 – (2·15 + 5) = 275.
= 310 – (2·15 + 5) = 275.
Оптимальный план перевозок записывается в виде таблицы 1.5:
Таблица 1.5
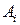 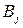
| 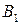
| 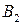
| 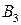
| Запасы |
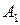
| ||||
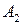
| ||||
| Потребность |
или матрицы 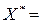
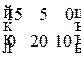 .
.
 2014-02-09
2014-02-09 6053
6053
