2014-02-09
981
Разбиения
Тема 3.2. Разбиения. Включения и исключения
Резюме по теме
Вопросы для повторения
1.Чем занимается комбинаторика?
2.Кем впервые был введен термин комбинаторика?
3.В чем заключается смысл правила суммы и произведения?
4.Что представляет собой выборка?
5.Когда используются перестановки?
6.Назовите отличие размещения от перестановки?
7.В чем особенность размещений с повторениями?
8.Что такое сочетание?
Показано назначение комбинаторики. Применение комбинаторики в менеджменте в явном виде практически не используется, но при применении статистики или же при решении задач линейного программирование аппарат комбинаторики приходится к месту. Рассмотрен принцип сложения и умножения. Показаны перестановки, размещения и сочетания.
Цель: ознакомиться с понятиями комбинаторики разбиения, включения и исключения.
Задачи:
1 Рассмотреть разбиения.
2 Рассмотреть полиномиальную формулу.
3 Рассмотреть формулы включения и исключения.
|
|
|
Подсчитаем число разбиений конечного множества Х, где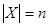 
, на k подмножеств Х 1, Х 2, …, Хk 
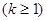таких, что каждое Хi содержит ni элементов, т.е.
, 
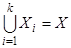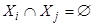при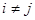 
, 
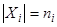, i =1, 2,.., k. (1)
Очевидно, что при этом n 1+ n 2+…+ nk = n. Отметим, что для некоторых номеров i возможно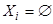 
. Число указанных разбиений при фиксированных ni обозначается 
.
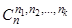Замечание. В данном случае набор подмножеств множества Х в разбиении является упорядоченным, т.е. Х 1, Х 2, …, Хk – упорядоченная последовательность множеств.
Лемма.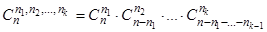 
.
Доказательство: Множество Х 1 может быть выбрано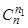 
. После выбора Х 1 множество Х 2 можно выбрать 
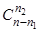способами (т.к. 
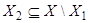и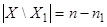 
) и т.д. Тогда по правилу произведения выбор упорядоченной последовательности множеств Х 1, Х 2, …, Хk можно произвести 
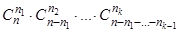способами.
Теорема 1.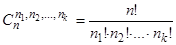 
.
Доказательство: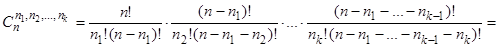 
[после сокращений]= 
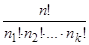, что и требовалось доказать.
Пример 2.
Требуется найти число размещений с повторениями из n элементов по k элементов, в которых первый элемент встречается ровно n 1 раз, второй элемент встречается ровно n 2 раз, …, k –ый элемент встречается ровно nk раз (n 1+ n 2+…+ nk = n).
Теорема 2. Число таких размещений равно .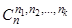
Доказательство. Каждому размещению указанного типа поставим в соответствие разбиение множества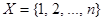 
номеров элементов в выборке на подмножества Х 1, Х 2, …, Хk, где Хi – множество номеров элементов i –го типа в выборке. Очевидно, что при этом выполняются условия (1). Указанное соответствие между размещениями данного типа и разбиениями, удовлетворяющими (1), является взаимно однозначным (биективным). Следовательно, в силу теоремы 1, теорема 2 верна.
