Задание двоичных функций формулами
Пусть имеется некоторый класс (т.е. множество) двоичных функций K. Он может быть как конечным, так и бесконечным. Обозначим через f1, f2,..., входящие в него функции, и пусть X = {x1, x2,...} множество двоичных переменных. Дадим индуктивное определение формулы над классом K.
1. Символ переменной xi, xiÎX есть формула над K.
2. Если f –обозначение некоторой функции от m переменных из класса K и Ф1,..., Фm - формулы над K то запись Ф = f(Ф1,..., Фm) есть формула над K
Таким образом, формулы – это записи, в которых используются символы переменных и функций из K. Если необходимо подчеркнуть, от каких переменных зависит формула Ф, то используют обозначение Ф(x1,...,xn), где x1,...,xn - это все переменные, участвующие в задании формулы Ф.
Установим теперь связь между формулами и двоичными функциями. Сначала заметим, что для произвольного набора значений переменных, входящих в формулу, можно, используя индуктивных характер определения, вычислять ее значение на этом наборе. Действительно, если значение формул Ф1,..., Фm, входящих в формулу Ф = f(Ф1,..., Фm), уже подсчитаны и равны соответственно b1,..., bm, biÎF2,то значение формулы Ф равно значению функции f(b1,..., bm). Поставим в соответствие каждой формуле Ф(x1,...,xn) функцию fФ(x1,...,xn), зависящую от тех же переменных, значения которой при всех значениях переменных совпадают со значениями формулы Ф(x1,...,xn).
Легко видеть, что одна и та же формула может быть использована для записи целого ряда функций. Например, формула x1 соответствует функциям
| x1 | f1 |
| x1 | x2 | f |
| x1 | x2 | x3 | f |
и.т.д. Поэтому естественным оказывается следующее определение.
Определение 1.3.1 Под функциями, реализуемыми формулой Ф понимается функция fФ , а также все функции, которые получаются из fФ удалением или добавлением несущественных переменных.
С другой стороны, одной функции может соответствовать множество различных формул. Например, рассматриваемые выше функции могут быть заданы любой из следующих формул:
x1, x1 ×(x1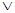 x2), x1
x2), x1 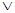 (x1× x2), x1
(x1× x2), x1 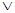 (x2×
(x2×  ),...
),...
Чтобы учесть эту неоднозначность введем понятие равносильности
формул.
Определение 1.3.2. Две формулы Ф1 и Ф2 называются равносильными (обозначается Ф1 = Ф2), если они реализуют одинаковые множества функций.
Замечание 1.3.3. Заметим, что для проверки равносильности формул Ф1 и Ф2 достаточно добавить к функции  те переменные, которые входят в Ф2, но не входят в формулу Ф1, а к функции
те переменные, которые входят в Ф2, но не входят в формулу Ф1, а к функции  добавить переменные из Ф1, которые не входят в формулу Ф2, а затем сравнить таблицы полученных функций.
добавить переменные из Ф1, которые не входят в формулу Ф2, а затем сравнить таблицы полученных функций.
Приведем два свойства, облегчающих проверку равносильности формул. Для их формулировки нам потребуется понятие подформулы.
Определение 1.3.4. Подформулой формулы Ф называется сама формула Ф; подформулой формулы f(Ф1,..., Фm) называется она сама, а также все подформулы формул Ф1,..., Фm.
Свойство 1.3.5. Если Ф1 - подформула формулы Ф, и Ф1 равносильна Ф2, то подформула Ф’, полученная из Ф путем замены Ф1 на Ф2 будет равносильна формуле Ф.
Свойство 1.3.6. Если формулы Ф1 и Ф2 равносильны, то, подставив одновременно в них вместо некоторых переменных любые формулы, получим в результате также равносильные формулы.
Основные способы задания двоичных функций.
(продолжение)
§2.1 нормальные формы двоичных функций.
Всюду в этом параграфе рассматриваются формулы над классом  . Обозначим через
. Обозначим через  функцию
функцию 
Очевидно, что  тогда и только тогда, когда
тогда и только тогда, когда  ,
, 
Определение 2.1.1 Элементарной конъюнкцией называются формулы вида  , где все переменные различны. Рангом элементарной конъюнкции называется число входящих в неё переменных.
, где все переменные различны. Рангом элементарной конъюнкции называется число входящих в неё переменных.
Непосредственно из определения 2.1.1 получаем, что элементарная конъюнкция  принимает единичное значение в том и только том случае, когда
принимает единичное значение в том и только том случае, когда  ,
,  . Этот факт запомним как свойство элементарных конъюнкций.
. Этот факт запомним как свойство элементарных конъюнкций.
Определение 2.1.2. Дизъюнктивной нормальной формой (ДНФ) называется формула вида  , где дизъюнкция берется по некоторым наборам
, где дизъюнкция берется по некоторым наборам  , и
, и  ,
,  .
.
Обозначим через  функцию, полученную из функции
функцию, полученную из функции 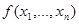 фиксацией первых
фиксацией первых  переменных значениями
переменных значениями  . Из следующей теоремы вытекает, что любую двоичную функцию можно задать с помощью ДНФ.
. Из следующей теоремы вытекает, что любую двоичную функцию можно задать с помощью ДНФ.
Теорема 2.1.3 (о разложении функции). При любом  ,
,  , двоичную функцию
, двоичную функцию 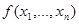 можно представить в виде:
можно представить в виде:
(2.1.4) 
Доказательство. Покажем, что функция, стоящая в левой и правой части равенства 2.1.4, принимает одинаковое значение при одинаковых значениях переменной. Пусть . Тогда в силу свойств элементарных конъюнкций значение функции из правой части равно
. Тогда в силу свойств элементарных конъюнкций значение функции из правой части равно  =
=  . Теорема доказана.
. Теорема доказана. 
Следствие 2.1.5
 (2.1.6)
(2.1.6)
Доказательство. Следует из теоремы 2.1.3, если положить 
Следствие 2.1.7
 (2.1.8)
(2.1.8)
Доказательство. Вытекает из следствия 2.1.5 при перенумерации переменных.
Замечание 2.1.9. Разложение (2.1.6) называется разложением Шеннона.
Следствие 2.1.10
 (2.1.11)
(2.1.11)
Доказательство. Следует из теоремы 2.1.3, если положить  .
.
Замечание 2.1.12. В разложении 2.1.11 можно опустить все элементарные конъюнкции, которым соответствуют нулевые значения функций. Полученная в результате формула имеет вид:
 (2.1.13)
(2.1.13)
Определение 2.1.14. Равенство (2.1.13) называется совершенной ДНФ (СДНФ) функции 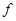 .
.
Как построить СДНФ функции 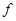 ?
?
СДНФ двоичной функции легко построить по ее табличному заданию. С этой целью для каждого набора аргументов  , на котором функция принимает единичное значение, строится элементарная конъюнкция ранга
, на котором функция принимает единичное значение, строится элементарная конъюнкция ранга 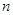 по правилу:
по правилу:
 (2.1.15)
(2.1.15)
Затем берется дизъюнкция всех построенных элементарных конъюнкций. Приведём пример:
Пример 2.1.16. Пусть функция 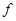 задана следующей таблицей:
задана следующей таблицей:
 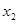 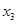 | 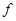 |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
Таблица 2.1.17
Построим для неё СДНФ:




Поэтому:





Заметим, что СДНФ является частным случаем ДНФ. В ней все элементарные конъюнкции имеют ранг 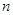 .
.
Отличительной особенностью СДНФ является то, что она однозначно определяется по функции 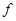 . Действительно, все элементарные конъюнкции в ней находятся во взаимно-однозначном соответствии с векторами
. Действительно, все элементарные конъюнкции в ней находятся во взаимно-однозначном соответствии с векторами  из области истинности функции:
из области истинности функции:  .
.
В отличие от СДНФ, ДНФ не однозначно соответствует функции. Так функция 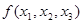 из предыдущего примера может быть записана в виде следующих ДНФ:
из предыдущего примера может быть записана в виде следующих ДНФ:

Аналогично ДНФ вводятся конъюктивные нормальные формы (КНФ). Они являются конъюнкциями элементарных дизъюнкций  и имеют вид
и имеют вид  , где конъюнкция берется по некоторым наборам
, где конъюнкция берется по некоторым наборам  ,
,  ,
,  . Как и в случае СДНФ можно показать, что функции
. Как и в случае СДНФ можно показать, что функции 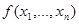 соответствует однозначно определенная КНФ(называемая совершенная КНФ), в которой все элементарные дизъюнкции имеют ранг
соответствует однозначно определенная КНФ(называемая совершенная КНФ), в которой все элементарные дизъюнкции имеют ранг 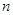 . Её можно получить из СДНФ функции
. Её можно получить из СДНФ функции  :
:  с помощью соотношений:
с помощью соотношений:  ,
,  . Из свойств 1.3.5 и 1.3.6 равносильных формул имеем:
. Из свойств 1.3.5 и 1.3.6 равносильных формул имеем:

 =
= =
= .
.
СКНФ функции 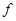 легко строится по её табличному зданию. Для функции
легко строится по её табличному зданию. Для функции 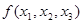 , заданной таблицей 2.1.17, получаем:
, заданной таблицей 2.1.17, получаем:




Поэтому





многочлен двоичной функции.
Будем рассматривать формулы над классом 
Определение 2.2.1. Многочленом Жегалкина (приведенным многочленом) называется представление двоичной функции 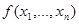 формулой вида:
формулой вида:
 , где
, где  .
.
Теорема 2.2.2. Для каждой двоичной функции существует единственный многочлен Жегалкина.
Доказательство. Покажем, что по таблице функции однозначно определяются коэффициенты  её многочлена Жегалкина. Воспользуемся методом неопределенных коэффициентов. Будем последовательно вычислять значения искомого многочлена на наборе из одних нулей, затем на наборе с одной единицей, затем – с двумя, и т.д. В результате получим систему:
её многочлена Жегалкина. Воспользуемся методом неопределенных коэффициентов. Будем последовательно вычислять значения искомого многочлена на наборе из одних нулей, затем на наборе с одной единицей, затем – с двумя, и т.д. В результате получим систему:

Из первого уравнения находим  , из второго
, из второго  ,…, из
,…, из  -
-  ,
,
из  -
-  ,…, из последнего
,…, из последнего  . Теорема доказана.
. Теорема доказана. 
Определение 2.2.3. Конъюнкции  , входящие в многочлен Жегалкина, называются одночленами. Степенью одночлена называется число входящих в него переменных (ранг конъюнкции). Степенью нелинейности (порядком) многочлена Жегалкина функции
, входящие в многочлен Жегалкина, называются одночленами. Степенью одночлена называется число входящих в него переменных (ранг конъюнкции). Степенью нелинейности (порядком) многочлена Жегалкина функции 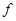 (обозначается
(обозначается  ) называют максимальную из степеней входящих в него многочленов.
) называют максимальную из степеней входящих в него многочленов.
Многочлен Жегалкина можно вычислять исходя из ДНФ или СДНФ
функции 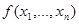 , выразив операции дизъюнкция и отрицание через операции конъюнкция и сложение по модулю два:
, выразив операции дизъюнкция и отрицание через операции конъюнкция и сложение по модулю два:

 2014-02-09
2014-02-09 1508
1508







