1. Найти точки, в которых 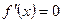 (стационарные) и точки, в которых
(стационарные) и точки, в которых 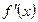 не существует. Это те точки, в которых функция может иметь экстремум (подозрительные на экстремум или критические).
не существует. Это те точки, в которых функция может иметь экстремум (подозрительные на экстремум или критические).
2. Разбиваем исследуемый интервал на частичные: 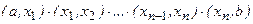 а,х1) – это интервалы монолитности функции.
а,х1) – это интервалы монолитности функции.
3. Находим знак производной в каждом из частичных интервалов. (Для этого достаточно узнать знак производной в любой точке интервала).
По изменению знака производной определяем точки экстремума.
Пример.
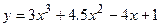
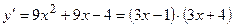
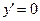 при
при 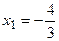 ,
, 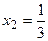 .
.
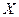
| 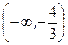
| -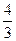
| 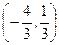
| 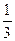
| 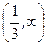
|
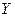
| | Max
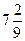
| ¯ | Min
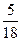
| |
| + | - | + |
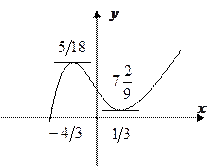
Если в точке 
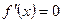 , но знака не меняет Þ функция не имеет ни max ни min, а соответственно при
, но знака не меняет Þ функция не имеет ни max ни min, а соответственно при 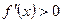 - возрастает, при
- возрастает, при 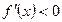 - убывает.
- убывает.
Теорема 3. (2-ой достаточный признак экстремума).
Пусть при 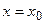
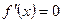 . Пусть, кроме того, $
. Пусть, кроме того, $ 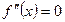 и непрерывна в некоторой окрестности точки
и непрерывна в некоторой окрестности точки 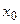 . Тогда
. Тогда 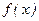 имеет max в точке
имеет max в точке 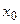 , если
, если 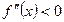 и
и 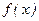 имеет min в точке
имеет min в точке 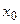 , если
, если 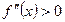 .
.
Доказательство.
1). Пусть 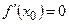 ,
, 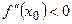 . То, что
. То, что 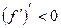 означает, что
означает, что 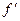 убывающая в окрестности
убывающая в окрестности 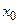 . Но по условию
. Но по условию 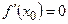 , т.е. при переходе через
, т.е. при переходе через 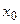 производная
производная 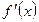 меняет знак с <+> на <-> Þ в точке
меняет знак с <+> на <-> Þ в точке 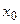
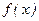 имеет max.
имеет max.
|
|
|
2). (Аналогично). 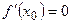 ,
, 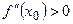 .
.
3). Если 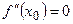 Þ характер
Þ характер 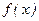 не известен и исследование нужно вести с помощью 1-ой теоремы.
не известен и исследование нужно вести с помощью 1-ой теоремы.
Вернемся к рассмотренному примеру: 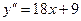
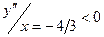

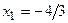 - max;
- max; 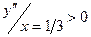

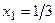 - min.
- min.
 2014-02-09
2014-02-09 420
420








