Скорость роста функций

Анализируя алгоритм можно стараться найти точное количество выполня­емых им действий. Но в большинстве случаев достаточно оценить асимптотику роста времени работы алгоритма (это делается на основе точной оценки) при стремлении раз­мера входа к бесконечности (asymptotic efficiency). Если у одного алгоритма асимптотика роста меньше, чем у другого, то в большинстве случаев он бу­дет эффективнее для всех входов, кроме, может быть, совсем коротких.

Сравнивая некоторую функцию ƒ с некоторым множеством функций, все алгоритмы можно сгруппировать по скорости роста. Существуют три категории:

1) Класс функций, растущих, по крайней мере, так же быстро, как ƒ, обозначается через Ω(ƒ) (читается как «омега большое»). Можно считать, что класс Ω(ƒ) задается указанием свой нижней границы: все функции из него растут, по крайней мере, так же быстро, как ƒ;

2) Класс функций, растущих не быстрее ƒ, обозначается O. Функция ƒ образует верхнюю границу для класса O (f)(читается как «о большое»);

3) Класс функций, растущих с той же скоростью, что и ƒ, обозначается Q(¦) ( читается как «тэта большое»). С формальной точки зрения этот класс представляет собой пересечение двух предыдущих классов.

Пусть время T (n) работы алгоритма на входах длины n есть Q(n²). Тогда найдутся такие константы c ₁, c ₂> 0 и такое число n ₀, что с ₁× n ² ≤ T (n) ≤ с ₂× n ² при всех n ≥ n ₀. Проще говоря, начиная с некоторого размера входа n ₀, функциональная зависимость T (n) может быть описана посредством n ² с точностью до константы, при этом «вилка» или диапазон возможных значений константы, способной обеспечить полное соответствие описания оригиналу, задается при помощи c ₁ и c ₂. Вообще, если g (n) – некоторая функция, то запись f (n) = Q(g (n)) означает, что найдутся такие c ₁, c ₂ > 0 и такое n ₀, что 0 ≤ с ₁× g (n) ≤ f (n) ≤ c ₂× g (n) для всех n ≥ n ₀. Запись f (n) = Q(g (n)) читается так: «эф от эн есть тэта от же от эн».

Следует также упомянуть, что если f ₁(n) = Q(g (n)) и f ₂(n) = Q(g (n)), то отсюда не следует f ₁(n) = f ₂(n)!

Определение Q(g (n)) предполагает, что функции f (n) и g (n) асимптотически неотрицательны (asymptotically nonnegative), т.е. неотрицательны для достаточно больших значений n. Если функции f и g строго положительны, то можно исключить n ₀ из определения (изменив константы c₁ и c₂ так, чтобы для малых n неравенство также выполнялось).

Если f (n) = Q(g (n)) то говорят, что g (n) является асимптотически точной оценкой (asymptotically tight bound) для f (n). На самом деле это отношение симметрично: из f (n) = Q(g (n)) следует g (n) = Q(f (n)).

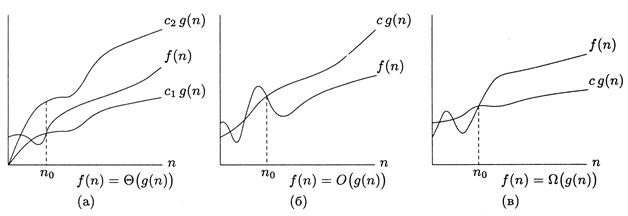
Рисунок 1.1 – Иллюстрации к определениям f (n) = Q(g(n)), f (n) = O(g(n)) и f (n) = W(g(n))

Запись f (n) = Q(g (n)) включает в себя две оценки: верхнюю и нижнюю. Их можно разделить. Говорят, что f (n) = O (g (n)), если найдется такая константа c > 0 и такое число n₀, что 0 ≤ f (n) ≤ c × g (n) для всех n ≥ n ₀. Говорят, что f (n) = W(g (n)), если найдется такая константа c > 0 и такое число n ₀, что 0 ≤ c × g (n) ≤ f (n) для всех n ≥ n ₀. Эти записи читаются так: «эф от эн есть о большое от же от эн», «эф от эн есть есть омега большая от же от эн».