Математический аппарат транспортной логистики

Несмотря на сложность использования математического аппарата в реальной деятельности специалист по логистике должен владеть им, поскольку умение решать математические задачи управления транспортом позволяют более системно и подробно понять принципы эффективного функционирования транспорта в рамках логистической системы.

Транспортная задача

(или задача прикрепления поставщиков к потребителям)

Данная проблема связана с распределением товаров между поставщиками (находящимися в пунктах производства) и потребителями (находящимися в пунктах назначения) таким образом, чтобы общая стоимость распределения была минимальной. Эта задача может быть решена либо с помощью методов линейного программирования, либо специального алгоритма решения транспортной задачи.

Имеется m поставщиков определенного вида продукции. Максимальные объемы возможных поставок заданы и равны соответственно a_i, i = 1, 2,…, m. Эта продукция используется n потребителями. Объемы потребностей заданы и равны соответственно b_j, j = 1, 2,…, n. Стоимость перевозки единицы продукции от i –го поставщика к j –му потребителю известна для всех i = 1, 2,…, m и всех j = 1, 2,…, n и равна c_ij. Требуется установить такие объемы перевозок x_ij от каждого поставщика к каждому потребителю, чтобы суммарные затраты на перевозки были минимальными и потребности всех потребителей были бы удовлетворены (если только общий объем возможных поставок покрывает общий объем потребностей).

Математическая модель этой задачи такова:

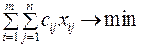
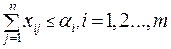
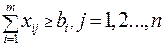
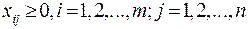
Очевидно, что эта задача линейного программирования с mn переменными и (m + n) непрямыми ограничениями.

В литературе описан ряд классических транспортных задач и методов их решения.

1. Задача о ранце. Здесь речь идет о собравшемся в поход путешественнике, который должен упаковать в ранец различные полезные предметы n наименований, причем может потребоваться несколько одинаковых предметов. Имеется m ограничений такого типа, как вес, объем, линейные размеры и т.д. При формулировке задачи место ранца может занять бомбардировщик, трюм или палуба корабля, складское помещение и т.д.

2. Задача о назначениях или задача выбора. Имеется n различных самолетов, которые требуется распределить между n авиалиниями. Известно, что на j –й авиалинии i –й самолет будет приносить доход c_ij. Требуется так распределить самолеты, чтобы максимизировать суммарный доход.

Эффективным методом решения задачи о назначениях является венгерский метод.

3. Задача о коммивояжере. Имеются города, пронумерованные числами 0, 1, 2,…, n. Выехав из города 0, коммивояжер должен объехать все остальные города, побывав в каждом из них по одному разу, и вернуться в исходный город. Известны расстояния c_ij между городами i и j (i = 1, 2,…, m; j = 1, 2,…, n). Требуется найти самый короткий маршрут.

4. Задача о четырех красках. В 1976 году была доказана замечательная теорема: любую географическую карту можно раскрасить, используя не более четырех различных красок. Тем самым была решена одна из наиболее знаменитых и старых математических проблем. Показательно, что обоснование этого результата проделано с помощью ЭВМ: после теоретических рассуждений осталось большое, но конечное число карт, относительно которых не было известно лишь то, можно ли их раскрасить четырьмя красками. С помощью ЭВМ был получен положительный ответ, который и дал окончательное решение проблемы.

Уточним формулировку задачи. Дана плоская географическая карта, на которой граница каждой страны представляет собой замкнутую непрерывную кривую. Две страны называются соседними, если у них есть общая граница – участок кривой определенной длины. Требуется так раскрасить данную карту в четыре цвета, чтобы соседние страны были раскрашены в разные цвета.