Количество расстановок скобок

Прежде чем применять динамическое программирование к задаче об умножении последовательности матриц, стоит убедиться, что простой перебор всех возможных расстановок скобок не даст эффективного алгоритма. Разобьём матрицы на группы по три; произведение для каждой группы можно вычислить двумя способами, так что для 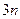матриц есть не менее 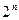вариантов. Следовательно, алгоритм полного перебора всевозможных вариантов не будет эффективным (полиномиальным).

1.3.2 Шаг 1: строение оптимальной расстановки скобок

Если мы собираемся воспользоваться динамическим программированием, то для начала должны описать строение оптимальных решений. Для задачи об умножении последовательности матриц это выглядит следующим образом.

Обозначим для удобства через 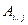матрицу, являющуюся произведением 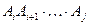. Оптимальная расстановка скобок в произведении 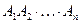разрывает последовательность между 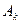и 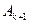для некоторого 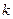, удовлетворяющего неравенству 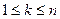. Иными словами, при вычислении произведения, диктуемом этой расстановкой скобок, мы сначала вычисляем произведения 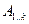и 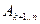, а затем перемножаем их и получаем окончательный ответ 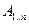. Стало быть, стоимость этой оптимальной расстановки равна стоимости вычисления матрицы 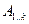плюс стоимость вычисления матрицы 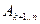плюс стоимость перемножения этих двух матриц.

Чем меньше умножений нам потребуется для вычисления 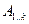и 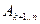, тем меньше будет общее число умножений. Стало быть, оптимальное решение задачи о перемножении последовательности матриц содержит оптимальные решения задач о перемножении её частей. Это и позволяет применить динамическое программирование.

1.3.3 Шаг 2: рекуррентное соотношение

Теперь надо выразить стоимость оптимального решения задачи через стоимости оптимальных решений её подзадач. Такими подзадачами будут задачи об оптимальной расстановке скобок в произведениях 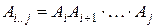для 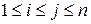. Обозначим через 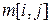минимальное количество умножений, необходимое для вычисления матрицы 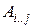, в частности, стоимость вычисления всего произведения 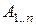есть .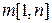

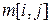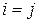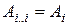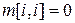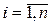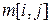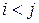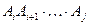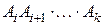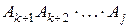Числа можно вычислить так. Если , то последовательность состоит из одной матрицы , и умножения вообще не нужны. Стало быть, для . Чтобы подсчитать для , мы воспользуемся информацией о строении оптимального решения, полученной на шаге 1. Пусть при оптимальной расстановке скобок в произведении последним идет умножение на , где 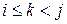. Тогда 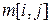равно сумме минимальных стоимостей вычисления произведени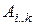и и 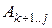плюс стоимость перемножения этих двух матриц. Поскольку для вычисления произведения 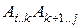требуется 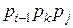умножений, то

.

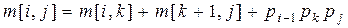В этом соотношении подразумевается, что оптимальное значение 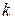нам известно; на деле это не так. Однако число 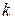может принимать всего лишь 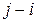различных значений: 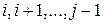. Поскольку одно из них оптимально, достаточно перебрать эти значения 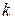и выбрать наилучшее. Получаем рекуррентную формулу:

(*)

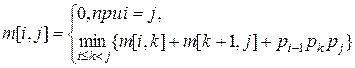Числа 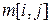- стоимости оптимальных решений подзадач. Чтобы проследить за тем, как получается оптимальное решение, обозначим через 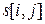оптимальное место последнего умножения, то есть такое 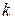, что при оптимальном вычислении произведения 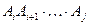последним идет умножение 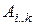на 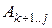Иными словами, 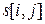равно числу 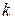, для которого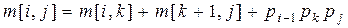

1.3.4 Шаг 3: вычисление оптимальной стоимости

Пользуясь соотношениями (16.2), теперь легко написать рекурсивный алгоритм, определяющий минимальную стоимость вычисления произведения 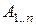(т.е. число 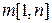). Однако время работы такого алгоритма экспоненциально зависит от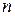, так что этот алгоритм не лучше полного перебора Настоящий выигрыш во времени мы получим, если воспользуемся тем, что подзадач относительно немного: по одной задаче для каждой пары 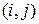, для которой 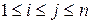, а всего 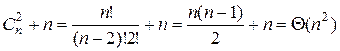. Экспоненциальное время работы возникает потому, что рекурсивный алгоритм решает каждую из подзадач по многу раз, на разных ветвях дерева рекурсии. Такое «перекрытие подзадач» - характерный признак задач, решаемых методом динамического программирования.

Вместо рекурсии мы вычислим оптимальную стоимость «снизу вверх» -

Заполняя таблицу 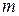, нужно последовательно решить задачи об оптимальной расстановке скобок для одного, двух,..., 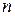сомножителей. В самом деле, соотношение (*) показывает, что число 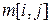— стоимость перемножения 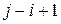матриц — зависит только от стоимостей перемножения меньшего (чем 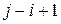) числа матриц.

Сначала нужно задать 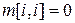для 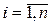: стоимость перемножения последовательности из одной матрицы равна нулю. Затем вычисляются (с помощью соотношения (*)) значени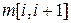я для 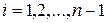— это минимальные стоимости для последовательностей длины 2. Следом рассчитываются значени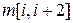я для 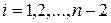— это минимальные стоимости перемножения последовательностей длины 3, и так далее.