Формирование нелинейных математических моделей

Обобщим ранее изложенные методы формирования математических моделей линейных схем на нелинейные схемы. Как и прежде, рассмотрим наиболее распространенные прямые методы формирования математических моделей – обобщенный метод узловых потенциалов, табличный, модифицированный табличный, модифицированный узловой и модифицированный узловой с проверкой.

При отыскании решения по постоянному току в цепи все катушки индуктивности закорачиваются (ветвь к.з.), а все конденсаторы исключаются, т.е. заменяются ветвью х.х.

Обобщенный метод узловых потенциалов. Прежде всего заметим, что уравнения для узловых потенциалов требуют, чтобы резисторы с нелинейным сопротивлением описывались в форме

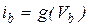. (7.14)

Индекс 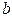будет обозначать напряжения и токи ветвей, а индекс 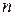используется для обозначения узловых переменных. Предполагается также, что все независимые источники представлены источниками тока.

Запишем закон Кирхгофа для токов ветвей и выразим напряжения ветвей через напряжения узлов:

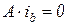, (7.15)

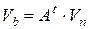. (7.16)

Разделив все ветви на две группы – ветви независимых источников тока и другие, можем переписать соотношение (7.15) в виде

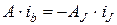(7.17)

или, обозначив узловые токи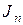

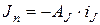, (7.18)

окончательно получим

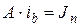. (7.17)

Подставив линейное уравнение ветви (7.14) в (7.17), получим

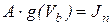, (7.20)

а, используя (7.16), можем записать обобщенную форму узловых уравнений нелинейной цепи

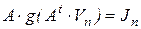. (7.21)

Для представления алгоритма Ньютона-Рафсона перепишем узловую систему нелинейной цепи в виде

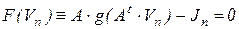. (7.22)

Дифференцированием сложной функции получаем матрицу Якоби узловой системы нелинейной цепи

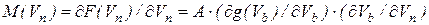. (7.23)

Вводя обозначение

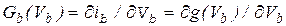(7.24)

и учитывая, что дифференцирование по 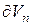соотношений для напряжений ветвей (7.16) дает

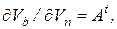(7.25)

получим выражение для Якобиана:

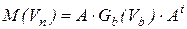. (7.26)

Как видим, вектор функций представляет собой систему узловых компонентных уравнений ветвей, а правило формирования Якобиана из проводимостей ветвей соответствует рассмотренному ранее правилу формирования матрицы проводимостей узловой системы уравнений.

В частном случае линейных сопротивлений соотношение (7.14) примет вид

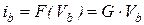. (7.27)

Вектор узловых токов с учетом (7.17) можно записать как

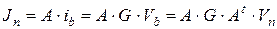, (7.28)

откуда вектор правой части системы уравнений Ньютона-Рафсона можно представить в виде

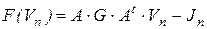. (7.27)

Выражение для производной тока ветви по напряжению ветви, представленное через разность узловых напряжений, запишется как

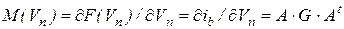. (7.30)

Откуда следует вывод, что компоненты вектора функции правой части системы уравнений Ньютона-Рафсона для линейных ветвей совпадают с линейными узловыми компонентными уравнениями ветвей, а Якобиан узловой системы уравнений для линейной цепи совпадает с дифференциальной матрицей проводимости.

Таким образом, формирование математической модели цепи по постоянному току узловым методом в виде линеаризованной итерационной системы Ньютона-Рафсона полностью совпадает с ранее рассмотренным случаем линейных цепей. Отличие заключается лишь в том, что формирование повторяется на каждом шаге итерации при новых уточненных значениях напряжений и токов. Компонентные уравнения нелинейных ветвей вектора функций и их производные по узловым напряжениям как проводимости нелинейных ветвей, включаемые в Якобиан, задаются аналитическими выражениями, вычисляемыми на каждом шаге итераций.

Обозначив через 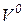начальное приближение вектора решений, распишем основные пункты алгоритма Ньютона-Рафсона в терминах обобщенного метода узловых потенциалов.

1. Установить 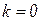и вычислить вектор узловых токов .

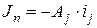2. Определить напряжения на ветвях .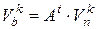

3. Найти токи нелинейных 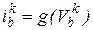и линейных 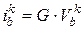ветвей.

4. Вычислить компонентную матрицу 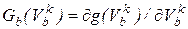. Для линейных ветвей элементы матрицы 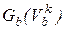совпадают со значениями их проводимостей.

5. Вычислить 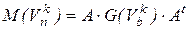и .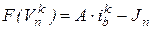

6. Решить уравнение Ньютона-Рафсона .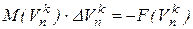

7. Уточнить вектор решений .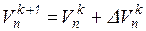

8. Если точность не достигнута, то установить 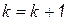и перейти к п.2.

Проиллюстрируем использование алгоритма Ньютона-Рафсона в обобщенном узловом методе на примере простой нелинейной цепи, используемой нами в начале раздела (рис. 7.3).

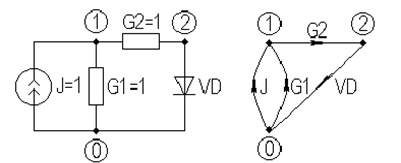
Рисунок 7.3 – Простая нелинейная цепь и ее граф

Пусть вектор начальных узлов напряжений определен как 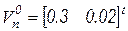. Уравнение диода опишем простейшей ВАХ .

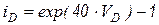Дополненная матрица инциденций ветвей схемы, согласно рис. 7.3, имеет вид

.

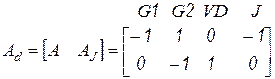Через матрицу инциденций ветвей независимых источников можно определить вектор узловых токов

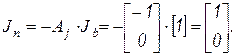
По матрице инциденций ветвей и начальному значению вектора узловых напряжений определим вектор начальных напряжений ветвей:

.

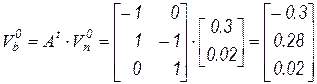Вектор токов ветвей, согласно компонентным уравнениям, определится как

.

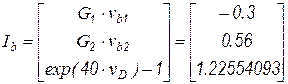Матрица дифференциальных проводимостей ветвей равна

.

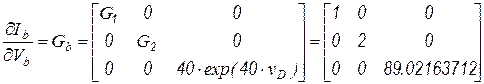Через матрицу инциденций и линеаризованную матрицу дифференциальных проводимостей ветвей определим линеаризованную узловую матрицу проводимости

.

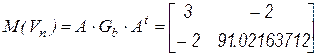Соответственно определяется вектор функций правой части системы Ньютона-Рафсона

.

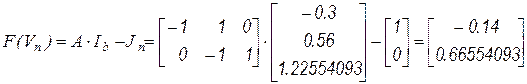В результате система уравнений Ньютона-Рафсона на основе обобщенного узлового метода, при заданных начальных значениях примет вид

.

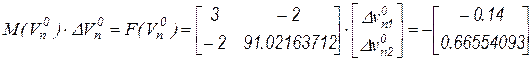Решение системы на первой итерации равно

.

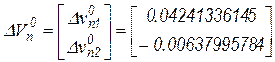Соответственно уточненные значения узловых напряжений после первой итерации при весовом коэффициенте 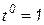будут равны

.

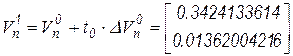Расчет на ЭВМ с точностью до пятого знака после запятой уже на четвертой итерации привел к результатам

; ; ; .

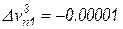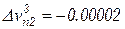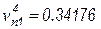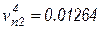Таким образом, получен тот же результат, что и в первом примере данного раздела.

При выводе соотношений алгоритма Ньютона-Рафсона применительно к узловому методу был использован классический подход, основанный на совокупности компонентных и топологических уравнений. При этом топологические соотношения отображались матрицей инциденций. Однако в обобщенном узловом методе, как ранее отмечалось при изложении метода, можно использовать и формальный подход. При этом матрицу Якоби и вектор функций правой части системы Ньютона-Рафсона можно сформировать напрямую по информации о ветвях схемы.

Матрица Якоби имеет такую же структуру, что и матрица проводимости. Проводимости линейных ветвей включаются в матрицу Якоби методом добавления в соответствии с узлами подключения. Нелинейная проводимость 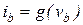, включенная между узлам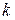и и 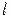, вызовет узловые токи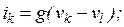 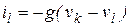, добавляемые в вектор функций. Дифференцируя эти соотношения по узловым напряжениям, получаем следующий фрагмент матрицы Якоби:

.

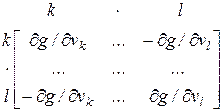Эти производные вычисляются при напряжениях, полученных на предыдущей итерации. Аналогично вносятся и другие нелинейные проводимости. Структура Якобиана фиксирована и дает возможность использовать алгоритмы, предназначенные для разряженных матриц при расчете сложных схем.

Правая часть системы уравнений Ньютона-Рафсона, определяемая соотношением 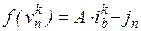, также может быть сформирована напрямую из компонентных уравнений ветвей методом добавления в соответствии с узлами подключения. Компонентные уравнения представляют собой токи линейных и нелинейных ветвей, подключенных к узлу, а также токи независимых источников тока, подключенных к узлу.

Так, диод, изображенный на схеме рис. 7.4, определит следующие элементы Якобиана и вектора правой части:

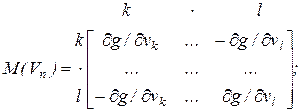
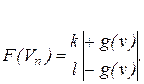
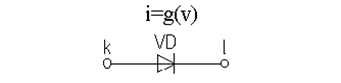
Рисунок 7.4 – Диод в качестве ветви схемы

Т.о., обобщенный узловой метод может рассматриваться как метод формирования математической модели нелинейной цепи.

Табличный метод. Перейдем к рассмотрению табличного метода формирования системы уравнений Ньютона-Рафсона.

Табличную систему как совокупность компонентных и топологических уравнений можно записать в общем виде

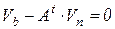, (7.31)

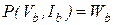, (7.32)

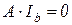. (7.33)

Компонентные уравнения (7.32) определяют связь между токами и напряжениями ветвей в неявной форме. Для линейных ветвей компонентные уравнения, как известно, принимают обобщенную линейную форму

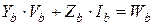. (7.34)

Соответственно правая часть уравнения Ньютона-Рафсона может быть записана в виде

,

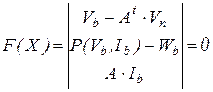где 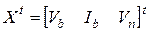. Матрица Якоби на 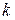-той итерации как производная вектора 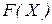по компонентам вектора 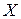будет иметь вид

,

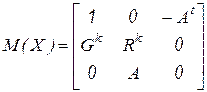где .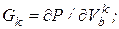

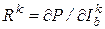Как видим, структура Якобиана совпадает с блочной формой табличной системы. Более того, в случае линейных цепей вместо компонентного уравнения (7.32) можно записать уравнение (7.34), и в результате дифференцирования вектора 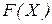убедимся, что Якобиан линейной цепи совпадает с традиционной матрицей коэффициентов табличной системы уравнений.

Система уравнений Ньютона-Рафсона, построенная на основе табличного метода, как обычно, имеет вид

,

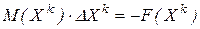где 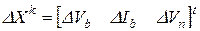. После определения вектора приращений уточняем вектор неизвестных

.

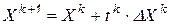Таким образом, табличный метод также может рассматриваться как метод формирования математической модели нелинейной цепи.

Модифицированный табличный метод. В модифицированном табличном методе, в отличие от табличного метода, с целью сокращения размерности системы уравнений (7.31)-(7.33) из рассмотрения исключается уравнение связи напряжений ветвей и узлов. При этом блочное уравнение (7.31) подставляется в уравнение (7.32), в результате чего получаем модифицированную табличную систему уравнений

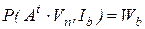, (7.35)

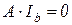. (7.36)

Следовательно, вектор правой части системы уравнений Ньютона-Рафсона, запишется в виде

,

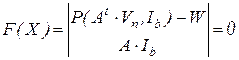где 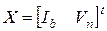– вектор неизвестных. Взяв производную на 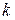-той итерации от вектора функций 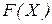, по компонентам вектора неизвестных 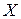получим Якобиан

,

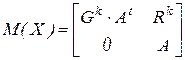где 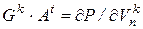; 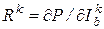. Как видим, структура Якобиана совпадает со структурой матрицы коэффициентов модифицированной табличной системы уравнений. Более того, в случае линейных цепей, воспользовавшись компонентным уравнением (7.34) вместо (7.32), после подстановки в него (7.31) получаем

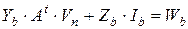(7.37)

вместо уравнения (7.35) и, дифференцируя полученную систему (7.37) и (7.36), убеждаемся, что Якобиан линейной цепи вырождается в матрицу коэффициентов модифицированной табличной системы уравнений.

Таким образом, система уравнений Ньютона-Рафсона как математическая модель нелинейной цепи может быть сформирована модифицированным табличным методом.

Модифицированный узловой метод. В модифицированном узловом методе, объединяющем достоинства узлового и табличного методов, как известно, все ветви цепи делят на три группы:

1) группа ветвей, представимых проводимостью, причем токи этих ветвей не определяются в результате решения;

2) группа ветвей, не представимых проводимостью либо представимых проводимостью, но необходимо определить токи этих ветвей;

3) группа ветвей независимых источников тока, вносимых в вектор узловых токов.

В обобщенном виде узловые уравнения ветвей первой и третьей групп и компонентные уравнения ветвей второй группы можно записать как

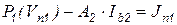, (7.38)

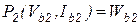, (7.37)

где ; ; .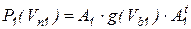

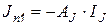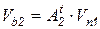Это позволяет записать вектор функций правой части системы уравнений Ньютона-Рафсона в виде

,

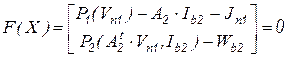где 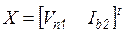– вектор неизвестных. Дифференцируя на 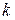-той итерации вектор функций по компонентам вектора неизвестных, получаем Якобиан системы уравнений Ньютона-Рафсона:

,

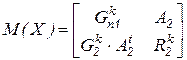где ; ; .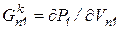

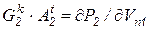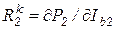Как видим, структура Якобиана аналогична структуре матрицы коэффициентов модифицированного узлового метода.

Для линейных цепей узловые уравнения ветвей первой и второй групп и компонентные уравнения второй группы вместо (7.38) и (7.37) запишутся в виде

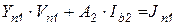, (7.40)

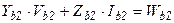, (7.41)

где ; ; .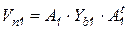

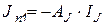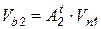Дифференцированием этих уравнений можно убедиться, что Якобиан линейной цепи совпадает с обычной матрицей коэффициентов модифицированной узловой системы уравнений.

Таким образом, модифицированный узловой метод можно рассматривать, как метод формирования математической модели нелинейной цепи.

Модифицированный узловой метод с проверкой. Модифицированный узловой метод с проверкой, как известно, отличается от модифицированного узлового метода тем, что с целью снижения порядка из системы уравнений исключаются те переменные, значения которых заранее известны. Речь идет в основном о токах ветвей холостого хода и напряжениях ветвей короткого замыкания, встречающихся в идеальных управляемых источниках. При этом ветви также разбиваются на три группы, но ветви второй группы, вносимые в дополнение матрицы проводимости, предполагается заносить в соответствии с таблицей. При этом, однако, структура матрицы коэффициентов остается аналогичной структуре матрицы коэффициентов модифицированного узлового метода.

В обобщенном виде узловые уравнения первой и второй групп и компонентные уравнения ветвей второй группы можно записать как

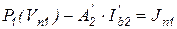, (7.42)

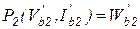, (7.43)

где 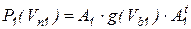; ; 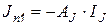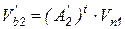. Это позволяет записать вектор функций правой части системы уравнений Ньютона-Рафсона в виде

,

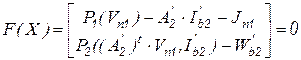где 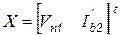– вектор неизвестных. Дифференцируя на 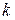-той итерации вектор функций по компонентам вектора неизвестных, получаем Якобиан системы уравнений Ньютона-Рафсона

,

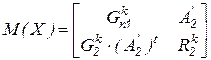где ; ; .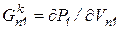

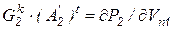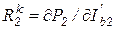Как видим, структура Якобиана аналогична структуре матрицы коэффициентов модифицированного узлового метода с проверкой.

Для линейных цепей узловые уравнения ветвей первой и второй групп и компонентные уравнения ветвей второй группы вместо (7.42) и (7.43), как известно, запишутся в виде

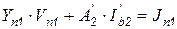, (7.44)

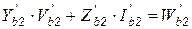, (7.45)

где ; ; .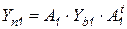

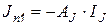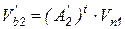Дифференцированием этих уравнений можно убедиться, что Якобиан линейной цепи совпадает с обычной матрицей коэффициентов модифицированной узловой системы с проверкой.

Т.о., модифицированный узловой метод с проверкой можно рассматривать как метод формирования математической модели нелинейной цепи.

Сходимость в диодно-транзисторных схемах. Применение метода Ньютона-Рафсона к расчету режимов диодно-транзисторных схем может привести к переполнению разрядной сетки ЭВМ. Это связано с тем, что в процессе итерационного поиска решения значения переменных, в частности напряжений, претерпевают значительные отклонения от начального значения. В то же время ВАХ-и диодов и транзисторов описываются в основном экспоненциальными зависимостями, небольшие изменения аргументов которых (напряжений на переходах) могут привести к весьма большим значениям функций (токов через переход), что и является основной причиной срыва итерационного процесса и переполнения разрядной сетки ЭВМ.

Поясним этот факт с помощью рис. 7.5, на котором изображена ВАХ диода.

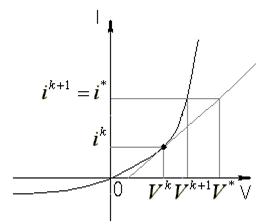
Рисунок 7.5 – ВАХ диода

Пусть ток диода описывается ВАХ диода вида 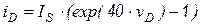. Предположим, что на 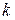-той итерации получена точка 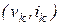и алгоритм предсказал на линеаризованной характеристике новую точку 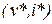. Согласно алгоритму, необходимо определить 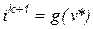, что может в случае экспоненциальной характеристики повлечь переполнение разрядной сетки ЭВМ. В качестве альтернативного шага определения 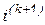предлагается брать горизонтальную проекцию на ВАХ точки пересечения вертикальной проекции точки 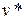. Тогда 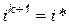, а инверсия вольтамперной характеристики дает 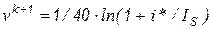. Горизонтальную проекцию на ВАХ можно использовать для всех напряжений на диоде превышающих 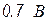. Напряжение 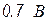соответствует 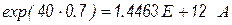, что вполне представимо в современных ЭВМ.

Другое эвристическое правило рекомендует использовать горизонтальную проекцию, при 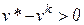, а вертикальную в противном случае.

Трудности могут возникнуть и при отрицательных смещениях на диоде, так как при итерациях вычисляются производные от ВАХ 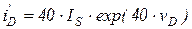, которые при 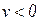могут оказаться слишком малыми. Во избежание этой ситуации при отрицательных напряжениях на диоде предлагается заменить ВАХ касательной при .

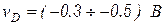Аналогично в качестве альтернативного подхода при прямом смещении на диоде, превышающем 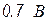, можно предложить заменять ВАХ на ее производную в точке .

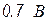Подобные способы преодоления переполнения разрядной сетки ЭВМ, в процессе итерационного поиска решения нелинейных систем уравнений, можно рекомендовать и в схемах на биполярных транзисторах, так как вольтамперные характеристики переходов также имеют экспоненциальную зависимость от напряжений на переходах.