Методы исследования макромоделей
Узловой метод в классической форме записи
Метод переменных состояния.
Тема 4: Модели метауровня
В зависимости от характера и сложности объекта исследования в высшем иерархическом уровне А (на метауровне) можно выделить различное количество подуровней.
На подуровне проектирования функциональных схем в качестве математических моделей элементов используют либо факторные макромодели, часто дополняемые необходимыми логическими, выражениями, либо макромодели в виде передаточных функций. В последнем случае имеет место функциональное моделирование. В качестве основной топологической матрицы, используемой при объединении математических моделей элементов в математическую модель системы, фигурирует матрица связей.
При наибольшей степени абстрагирования от физических свойств элементов и сигналов непрерывная система вырождается в дискретную, в математической модели системы остаются только логические переменные и связи между ними. Такие логические модели находят применение при проектировании функциональных схем цифровых вычислительных машин и устройств дискретной автоматики. Математический аппарат логического моделирования — математическая логика.
Аппарат функционального моделирования применяют при проектировании не только функциональных, но и принципиальных схем, и потому функциональное моделирование занимает положение связующего звена между уровнями А и Б в иерархическом проектировании. На подуровне проектирования структурных схем математические модели систем должны отражать информационные связи между элементами. Типичные математические модели систем этого подуровни формируются на основе статистических закономерностей поступления и обработки информации, при этом применяют такие разделы теории вероятностей, как теория очередей и теория массового обслуживания.
Функциональное моделирование появилось и получило широкое распространение в рамках традиционных немашинных методик исследований.
Основой моделирования на функциональном уровне является использование аппарата передаточных функций. То есть, вместо двух типов фазовых переменных, используемых на микро и макроуровнях, в функциональных моделях фигурируют переменные одного типа, называемые сигналами. Физический смысл сигнала конкретизируется в каждом конкретном случае исходя из особенностей задачи. При этом модель каждого элемента (модели микро и макроуровня) представляют в виде уравнения вход – выход, т.е. в виде 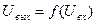 .
.
Естественно, что при этом используются достаточно серьезные допущения и ограничения. В частности это требование безинерционности, линейности математических моделей инерционных элементов.
При выполнении требования линеаризации математических моделей инерционных элементов процессы в инерционном элементе описывают системой линейных дифференциальных уравнений:
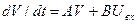 ,
, 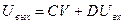 .
.
Здесь: V — вектор переменных состояния; 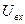 и
и 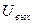 - векторы входных и выходных сигналов; А, В, С и D - постоянные матрицы.
- векторы входных и выходных сигналов; А, В, С и D - постоянные матрицы.
Линейность системы позволяет линеаризировать систему уравнений, перейдя от оригиналов к изображениям с помощью преобразования Лапласа:
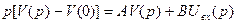 ;
;
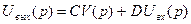 .
.
Из первого имеем 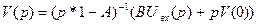 , где 1 — единичная матрица того же порядка, что и матрица А.
, где 1 — единичная матрица того же порядка, что и матрица А.
Подставляя во второе, получаем
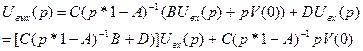 .
.
Матрицу 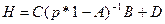 называют матрицей передаточных функций, ее элемент
называют матрицей передаточных функций, ее элемент 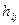 равен отношению изображения сигнала на
равен отношению изображения сигнала на 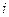 выходе к изображению сигнала на
выходе к изображению сигнала на 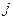 входе. Элементы системы, называемые при функциональном моделировании звеньями, часто рассматривают как объекты с одним входом и одним выходом. Тогда математическая модель элемента есть простое соотношение, связывающее входную и выходную фазовые переменные:
входе. Элементы системы, называемые при функциональном моделировании звеньями, часто рассматривают как объекты с одним входом и одним выходом. Тогда математическая модель элемента есть простое соотношение, связывающее входную и выходную фазовые переменные: 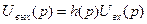 , где h(р) — передаточная функция.
, где h(р) — передаточная функция.
Объединение математических моделей элементов в математическую модель системы осуществляется при функциональном моделировании отождествлением тех входных и выходных величин, которые соответствуют соединяемым входам и выходам (информация о соединениях задается матрицей связей). Столь простое правило построения математической модели системы не может быть строго обосновано; оно вытекает из допущения, что передаточные функции всех звеньев h(р) не зависят от характера и величины нагрузки.
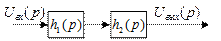 Пусть имеем два звена с передаточными функциями
Пусть имеем два звена с передаточными функциями 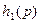 и
и 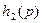 , соединенные последовательно. Отождествляя
, соединенные последовательно. Отождествляя 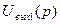 с
с 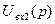 , получаем
, получаем 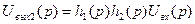 .
.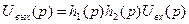
Последнее соотношение и принимается в качестве математической модели рассмотренной системы. При этом в формуле не учтено изменение функции 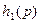 , происшедшее при подключении второго звена к выходу первого.
, происшедшее при подключении второго звена к выходу первого.
Второе серьезное допущение функционального моделирования, заключающееся в не учете влияния нагрузки, ограничивает область его применения системами из элементов с большими запасами по нагрузочной способности.
 Очевидно, что если система имеет обратные связи, то математическая модель физической системы превращается в уравнение или в систему уравнений. Так, для простого примера обратной связи, имеем
Очевидно, что если система имеет обратные связи, то математическая модель физической системы превращается в уравнение или в систему уравнений. Так, для простого примера обратной связи, имеем 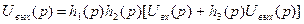 .
.
Макромодели в виде передаточных функций чаще всего получаются с помощью теоретического подхода путем линеаризации полной математической модели и определения матрицы передаточных функций через обращение матрицы 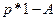 .
.
 2014-02-12
2014-02-12 1769
1769
