2014-02-12
670
Ротор
По определению проекция (rot a) n ротора векторного поля a в некоторой точке P на направление фиксированного вектора n представляется формулой:
.
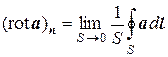Следовательно, мы можем получить проекцию rot a на направление вектора e 1, вычислить циркуляцию вектора a вдоль контура MM 2 N 1 M 3 M (см. рис. 9.1) и разделив ее на d s1. Представим эту циркуляцию в виде суммы четырех слагаемых, отвечающих отрезкам MM 2, M 2 N 1, N 1 M 3 и M 3 M, и вычислим каждое слагаемое отдельно. Начнем с первого из них. Проекция вектора a на направление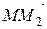 
равна a 2, следовательно, циркуляция вектора a вдоль 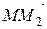(с точностью до бесконечно малых величин первого порядка относительно d s1) равна
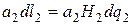. (9.14)
Циркуляция вдоль N 1 M 3 отличаются от только что полученного выражения тем, что на N 1 M 3 третья координата равна q 3+ dq 3, а не q 3, как на MM 2, и, кроме того, направление отрезка N 1 M 3 противоположно направлению e 2. Поэтому циркуляция вдоль N 1 M 3 равна
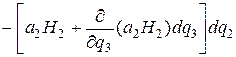. (9.15)
Аналогично получаем для циркуляции вдоль M 2 N 1 и N 3 M выражения
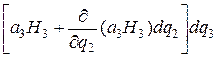(9.16)
и
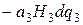. (9.17)
Сложив величины (9.14)-(9.17), получим, что циркуляция вектора a вдоль контура MM 2 N 1 N 3 M равна
|
|
|
.
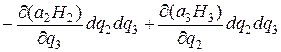Деля полученное выражение на H 2 H 3 dq 2 dq 3, т.е. на площадь грани MM 2 N 1 M 3, получим, что компонента (rot a)1 вектора rot a в направлении базисного вектора e 1 равна
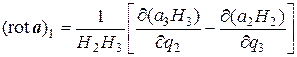. (9.18)
Аналогично вычисляются две другие компоненты:
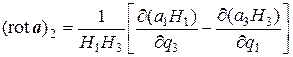, (9.19)
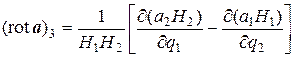. (9.20)
Символически это можно записать в виде
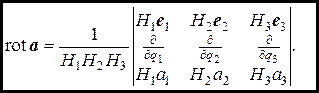(9.21)
Оператор Лапласа DU функции U определяется формулой
.
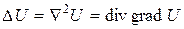Пользуясь формулами для градиента и дивергенции, находим
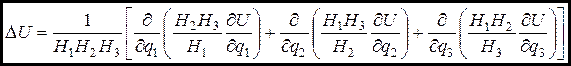. (9.22)
