Метод потенциалов

В соответствии с введенным понятием потенциалов и с учетом связей между моделями двойственных задач каж­дому поставщику (ограничению по запасам) поставим в соответствие потенциал 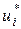, 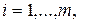а каждому по­требителю (ограничению по спросу) – потенциал ,

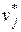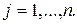
Согласно теореме о потенциалах, каждой занятой клет­ке будет соответствовать уравнение 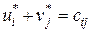. Так как всех занятых клеток должно быть т+п- 1, т. е. на еди­ницу меньше числа потенциалов, то для определения чи­сел 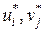необходимо решить систему из т+п- 1 уравне­ний 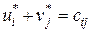с т+п неизвестными. Система неопреде­ленная, и, чтобы найти частные решения, одному из потен­циалов придаем произвольное числовое значение, тогда остальные потенциалы определяются однозначно. Для облегчения расчетов одному из потенциалов придают обычно значение, равное нулю.

Для исследования плана на оптимальность для каждой свободной клетки проверяется условие 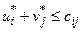. Если хотя бы одна свободная клетка не удовлетворяет данному условию, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка, для которой разность (оценка) между тарифом клетки и суммой потенциалов наименьшая, т. е.

.

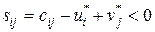Экономически оценка показывает, на сколько денежных единиц уменьшатся транспортные издержки от загрузки данной клетки единицей груза.

Если для всех свободных клеток оценки 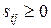, то опорный план перевозок является оптимальным.

Итак, если для опорного плана перевозок указанное условие оптимальности не выполняется, то за счет загруз­ки свободной клетки с отрицательной оценкой план пере­возок улучшается. Для наиболее перспективной свобод­ной клетки строится замкнутый цикл с вершинами в за­груженных клетках. Вершинам этого цикла условно приписываются знаки: свободной клетке – плюс, следую­щей по часовой или против часовой стрелки занятой клет­ке – минус, следующей – снова плюс и т. д. Из поставок в клетках цикла с «отрицательными» вершинами выби­рается наименьшее количество λ груза, которое и переме­щается по клеткам этого цикла: прибавляется к постав­кам в положительных вершинах и вычитается из поставок в отрицательных вершинах, в результате чего баланс цикла не нарушится.

В общем случае цикл представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся под прямым углом. Каждое звено соединяет две клетки строки (столбца). Цикл включает одну свободную клетку, остальные клетки цикла заняты. В цикле всегда четное число клеток. Для свободной клетки всегда можно постро­ить единственный цикл. Если из занятых клеток образу­ется цикл, то план перевозок не является опорным. Цикл строится лишь для свободной клетки.

Сформулируем алгоритм решения ТЗ методом потен­циалов:

1) построить опорный план по одному из правил;

2) вычислить потенциалы поставщиков и потребителей, решив систему уравнений ви­да ;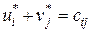

3) вычислить оценки для всех свободных клеток по формуле 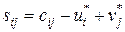. Если все оценки больше либо равны нулю, то полу­ченный план является оптимальным. При этом, если все 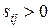, то полученный оптимальный план единственный. В случае, если хотя бы одна оценка 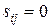, имеем бесчис­ленное множество оптимальных планов с одним и тем же значением целевой функции.

Пример 5.3. Проверим, является ли план, полученный в примере 5.2, оптимальным.

Решение. Для определения потенциалов составляем систему уравнений:

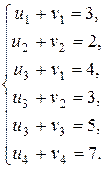
Положим, например, и ₁ = 0, тогда.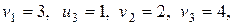

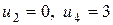Потенциалы проставлены в табл. 5.5. Их можно вычислять и непо­средственно в таблице, не выписывая систему уравнений. Ведь если известны потенциал и тариф занятой клетки, то из соотношения 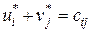легко определить неизвестный потенциал (из суммы вычесть известное слагаемое, получим неизвестное слагаемое). Роль суммы в данном равенстве играет тариф .

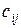Таблица 5.5

							и 1 = 0
			-
					+
		+			-

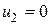
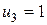
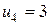
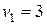
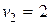
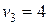
Определим оценки свободных клеток:

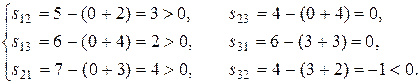
Перспективной является клетка (4; 2) с оценкой –1. Строим для нее цикл непосредственно в таблице. В цикл войдут клетки (3; 2), (3; 3), (4; 3). Наименьшее количество груза, стоя­щее в вершинах цикла с отрицательным знаком, λ = min (400, 500) = 400. В результате смещения λ по циклу получим новый план (табл. 5.6).

Таблица 5.6

							и 1 = 0
			-	+
			+		-

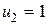
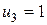
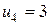
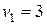
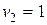
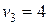
Стоимость перевозок:

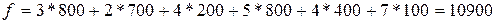руб.

Для нового плана определяем новые потенциалы и оценки свобод­ных клеток:

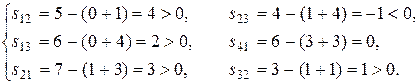
Перспективной является клетка (2; 3) с оценкой –1. Строим для нее цикл непосредственно в таблице. В цикл войдут клетки (2; 2), (4; 2), (4; 3). Наименьшее количество груза, стоя­щее в вершинах цикла с отрицательным знаком, λ = min (700, 100) = 100. В результате смещения λ по циклу получим новый план (табл. 5.7).

Таблица 5.7

							и 1 = 0

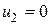
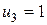
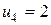
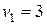
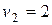
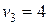
Стоимость перевозок:

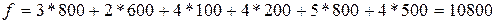руб.

Для нового плана определяем новые потенциалы и оценки свобод­ных клеток:

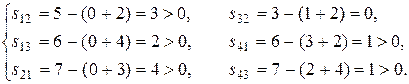
Оценки всех свободных клеток неотрицательны, следовательно, по­лученный план является оптимальным.

Минимальные транспортные издержки для этого плана: 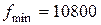руб.

Поскольку среди оценок есть равная нулю, то оптимальный план не единственный.

6. матричная теория игр

6.1. Область применения аппарата теории игр

Достаточно часто решения приходится принимать в условиях неопределенности, то есть в таких условиях, когда или процесс выполнения операции является неопределенным, или нам сознательно противодействует противник, или нет ясных и четких целей (задач) операции. Следствием неопределенности является то, что успех операции зависит не только от наших решений, но от чьих-то решений или действий.

В целом ряде задач приходится анализировать ситуации, в которых сталкиваются какие-то противоборствующие стороны (две или более), каждая из которых преследует свою цель, причем результат любого мероприятия каждой из сторон зависит от того, какие действия предпримет противник. Такие ситуации называют конфликтными, их изучением занимается теория игр. Теорию игр можно определить как теорию математических моделей принятия решений в условиях конфликта.

Среди задач, требующих применения теории игр, можно назвать следующие:

– анализ конфликтных ситуаций в военных и экономических областях (простым экономическим примером конфликтной ситуации, для описания которой применяется теория игр, является конкурентная борьба торговых фирм или промышленных предприятий);

– обменные и торговые операции:

– анализ и проектирование иерархических структур управления и экономических механизмов (например, анализ различных моделей стимулирования);

– анализ целесообразности права первого хода, взаимной информативности, возможности блефовать;

– анализ коалиционного поведения;

– ряд других задач.

Теория игр предназначена для получения решений в играх, которые играются только один раз. Если игра повторяется, то надо использовать статистические методы. В единичной, неповторяющейся игре теория игр позволяет выбрать одно определенное «лучшее» решение из множества возможных решений, либо получить характеристики того случайного механизма, с помощью которого один раз выбирается какое-то одно из возможных решений.