Лекция 6
Результатом пересечения плоскости и многогранной поверхности является в общем случае плоская ломаная линия, которая может быть построена по ее вершинам или сторонам. Первый вариант построения сводится к задаче пересечения прямой с плоскостью, т. е. пересечению ребер многогранника с заданной плоскостью: 1 = SA ∩ Σ, 2 = SB ∩ Σ, 3 = SA ∩ Σ. Второй вариант к пересечению плоскостей, т. е. граней многогранника с плоскостью сечения: p = SAB ∩ Σ, l = SAC ∩ Σ, q = SBC ∩ Σ (рис.42, а).
Выбор способа построения определяется в зависимости от графических условий конкретной задачи.

Рис. 42
На рис. 42, б показано построение на комплексном чертеже линии пересечения фронтально проецирующей плоскости с поверхностью пирамиды. Точки 1, 2 и 3 построенного треугольника определены как точки пересечения ребер пирамиды SA, SB и SC с заданной плоскостью Σ, т. е. задача решена с использованием первого варианта построения.
В том случае, если плоскость сечения занимает общее положение относительно плоскостей проекций, рекомендуется преобразовать ее в проецирующую, используя один из рассмотренных ранее способов преобразования чертежей, так как в общем положении не всегда удается сразу оценить положение плоскости сечения относительно заданной поверхности и вид сечения. Например, если задана плоскость и треугольная пирамида (четырехгранник) в общем положении, то сразу по чертежу трудно оценить, какая фигура получается в пересечении – треугольник или четырехугольник.
|
|
|
В результате пересечения плоскости с кривыми поверхностями получаются плоские кривые линии. Рассмотрим эту тему на примере пересечения плоскости с поверхностями вращения: цилиндрической, конической и сферической, которые являются поверхностями второго порядка. Следовательно, в пересечении их с плоскостью получаются кривые второго порядка – эллипс, гипербола и парабола. И как частный случай – точка, прямая и окружность [2].
Пересечение цилиндрической поверхности вращения с определенным образом ориентированными относительно нее проецирующими плоскостями показаны на фронтальных проекциях комплексного чертежа (рис. 43, а и б).
1. Плоскость (Δ) пересекает все образующие цилиндрической поверхности, т. е. не параллельна ни одной из них. Результатом пересечения является плоская, замкнутая кривая линия второго порядка – эллипс (см. рис. 43, а). В частном случае (Δ ^ i) имеем – окружность.
2. Плоскость (Ω) параллельна образующим цилиндрической поверхности, т. е. не пересекает ни одну из них. В этом варианте в пересечении получаем две прямые m и n (см. рис. 43, б). Если заданная плоскость касательная к поверхности, то в результате имеем одну прямую.
|
|
|

Рис. 43
Пересечение конической поверхности вращения с определенным образом ориентированными относительно нее проецирующими плоскостями показаны на фронтальных проекциях комплексного чертежа (рис. 44 а, б и в).
1. Плоскость (Γ) пересекает все образующие конической поверхности, т. е. она не параллельна ни одной из них. В этом варианте сечение представляет собой плоскую, замкнутую кривую линию второго порядка – эллипс (см. рис. 44, а). В частных случаях имеем окружность (Γ ^ i) и точку S (Γ Ì S).
2. Плоскость (Λ) параллельна одной образующей конической поверхности (l). В этом случае сечение представляет собой плоскую, незамкнутую кривую линию второго порядка – параболу, так как заданная плоскость пересекает только одну из двух пол конической поверхности, расположенных по разные стороны от вершины (S) (см. рис. 44, б). В частном случае, когда плоскость проходит через вершину конической поверхности (Λ Ì S) получаем в пересечении прямую (l)
3. Плоскость (Σ) параллельна двум образующим конической поверхности, например, q и p. В этом варианте в сечении получается плоская, незамкнутая кривая линия второго порядка – гипербола, состоящая из двух ветвей, так как заданная плоскость пересекает обе полы конической поверхности (см. рис. 44, в). В частном случае имеем прямые (q и p), если плоскость проходит через вершину конической поверхности(Σ Ì S).
При пересечении плоскости со сферой получается окружность, которая вырождается в точку в момент касания плоскости и сферы. Если плоскость проходит через центр сферы, то в пересечении получится окружность, диаметр которой равен диаметру сферы. Такую окружность называют меридианом.
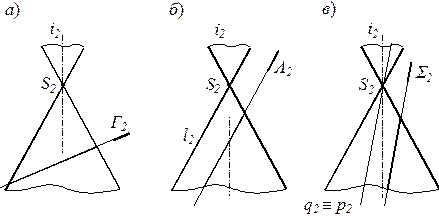
Рис. 44
 2014-02-09
2014-02-09 897
897








