2014-02-13
969
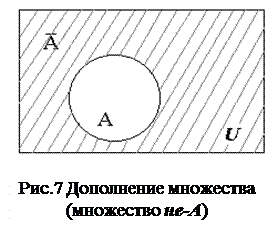
Опр.2.3.5 Дополнением множества А называется разность U\А.. Обозначается, А’ или А и читается «не-А». Иначе, дополнением множества А называется множество А’, состоящее из всех элементов, не принадлежащих множеству А.
Теперь укажем основные свойства изученных выше операций над множествами:
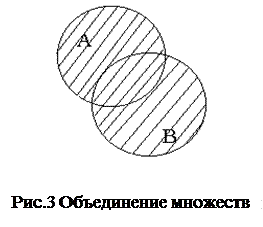
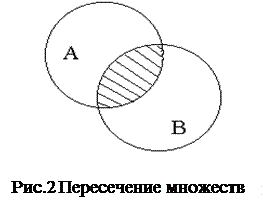
| Свойства операции пересечения: 1) АÇА=А; 2) АÇÆ=Æ; 3) АÇА’=Æ; 4) АÇ U =А; 5) АÇВ=ВÇА. | Свойства операции объединения: 1) АÈА=А; 2) АÈÆ=А; 3) АÈА’= U; 4) АÈ U = U; 5) АÈВ=ВÈА. |
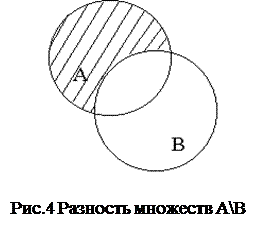
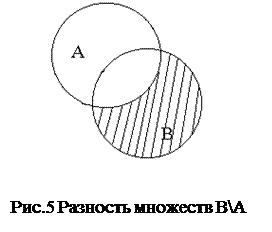
| Свойства операции разности: 1) А\А=Æ; 4) А\ U =Æ; 2) А\Æ=А; 5) U \А=А’; 3) А\А’=А; 6) Æ\А=Æ; 7) А\В ¹ В\А. |
Справедливы равенства (АÈВ) =АÇВ; (АÇВ) =АÈВ (3).
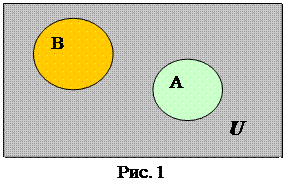Для наглядного представления (графического изображения) множеств и результатов операций над ними удобно пользоваться так называемыми диаграммами Эйлера-Венна (кругами Эйлера).
При этом множества изображаются на плоскости в виде замкнутых кругов, а универсальное множество в виде прямоугольника. Элементы множества – точки внутри соответствующего круга.
|
|
|
 |
 |  | ||
 |  | ||
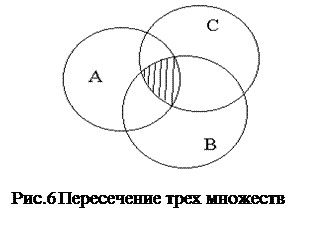
В заключение приведем еще одну формулу для подсчета числа элементов в объединении трех множеств (для общего случая их взаимного расположения, показанного на рис.6):
m (АÈВÈС) = m (А) + m (В) + m (С) - m (АÇВ) – m (АÇС) –
– m (ВÇС) + m (АÇВÇС) (4).
§ 3. Элементы комбинаторики. Соединения без повторений
и с повторениями. Правила суммы и произведения.
Комбинаторика – теория соединений – изучает некоторые операции над конечными множествами, как упорядочение множества и разбиение множества, интересуется расположением элементов в множестве, выясняет, сколькими способами можно расположить элементы множества в том или ином порядке. Это приводит к понятиям перестановок, размещений и сочетаний. Основными задачами комбинаторики являются: 1) определение вида соединения; 2) подсчет числа соединений.
