Уравнение Шрёдингера

В развитие идеи де Бройля о волновых свойствах частиц Шрёдингер в 1926 году предложил своё знаменитое уравнение. Шрёдингер сопоставил движущейся микрочастице комплексную функцию координат и времени, которую он назвал волновой функцией и обозначил греческой буквой «пси» 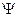. Её принято называть пси-функцией.

Состояние микрочастицы характеризует пси-функция, которая является решением уравнения Шрёдингера:

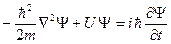. (1.5)

Здесь m – масса частицы, i – мнимая единица, 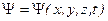, 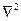– оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых частных производных по координатам:

.

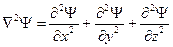Символом U в уравнении (1.5) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу. В случае, когда U не зависит явно от времени, она имеет смысл потенциальной энергии частицы.

В этом случае уравнение (1.5) преобразуется к виду

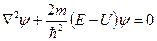. (1.6)

Здесь 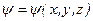, Е – полная энергия частицы.

Уравнение (1.6) называется уравнением Шрёдингера для стационарных состояний.

В теории дифференциальных уравнений доказывается, что уравнения вида (1.6) имеют решения, удовлетворяющие стандартным условиям, налагаемым на 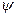-функцию, при дискретных значениях энергии Е. Таким образом, квантование энергии получается из основных положений квантовой механики без каких-либо дополнительных предположений.