Условный закон распределения, условная плотность

В задачах практики, имея дело со случайными векторами, часто приходится определять распределение одних координат случайного вектора при известных значениях других – так называемые условные распределения.

Определение. Пусть 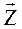=(X,Y). – случайный вектор. Условным законом распределения одной из координат этого вектора называется ее закон распределения, вычисленный при условии, что другая случайная координата приняла определенное значение (или попала в какой-то интервал). ▄

Для любого типа случайных величин (дискретных, непрерывных) функция распределения F(x,y) может быть записана в виде:

F(x,y)=P{X<x;Y<y}=P{X<x}P{Y<y|X<x}=F₁(x)P{Y<y|X<x}

Условная вероятность P{Y<y|X<x} - вероятность события {Y<y} при условии, что величина X приняла значение меньшее, чем x, может быть названа условной функцией распределения случайной величины Y при условии X<x; обозначим ее

P{Y<y|X<x}=F₂(y|X<x).

Тогда

F(x,y)=F₁(x)F₂(y|X<x) (1)

Если в качестве "первой" координаты взять случайную величину Y, то по аналогии с (1), получим:

F(x,y)=F₂(y)F₁(x|Y<y) (2)

На практике применяют другой вид условного закона: закон распределения одной из случайных величин при условии, что другая приняла вполне определенное значение. Вычислим такой закон для системы двух дискретных случайных величин (X,Y). Он образован условными вероятностями, представляющими собой вероятность того, что случайная величина X примет значение x_i, при условии, что Y=y_i (или, наоборот, вероятность того, что случайная величина Y примет значение y_i, при условии, что X=x_i). Эти условные вероятности найдем, вспомнив следующую формулу: а именно, как определяется условная вероятность события В при наличии А:

.

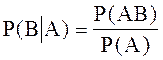Применяя эту формулу, найдем условную вероятность того, что случайная величина Y=y_j при условии, что X=x_i

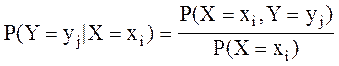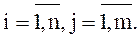, (3)

и, аналогично,

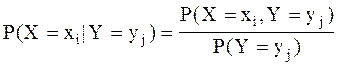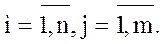, (4)

Совокупность вероятности (3) для 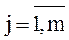представляет собой условный ряд распределения случайной величины Y при условии X=x_i (аналогично и для формулы (4)). Этот ряд распределения обладает свойством обычного ряда распределения: сумма образующих его вероятностей равна 1.

Теорема умножения плотностей. Рассмотрим систему двух зависимых непрерывных случайных величин (X,Y). Можно доказать, что их совместная плотность равна произведению плотности одной из них на условную плотность другой при заданном значении первой

f(x,y)=f₁(x)f₂(y|x) (5)

или, что равносильно,

f(x,y)=f₂(y)f₁(x|y) (6)

где f₂(y|x) - условная плотность случайной величины Y при условии X=x, f₁(x|y) - аналогично.

Эти формулы (5) и (6) можно получить, используя правило умножения вероятностей в схеме событий, а также элемент вероятности f(x,y)dxdy.

Из формул (5) и (6) вытекают формулы, выражающие условные плотности распределения:

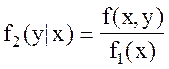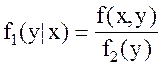; , (7)

т.е. чтобы получить условную плотность распределения одной из случайных величин, входящих в систему, надо разделить совместную плотность на плотность распределения другой случайной величины.

Аналогичные формулы для векторной случайной величины 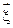= (x₁, x₂)

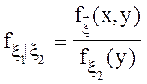Þ для случайного вектора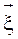

Ранее полученные формулы (1)-(7) можно обобщить на n-мерный случай.

Для дискретных случайных величин имеем:

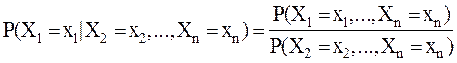(8)

Для непрерывных случайных величин условная плотность вычисляется по формуле:

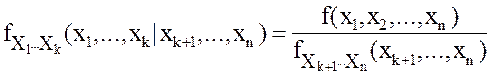(9)

т.е. условной плотностью распределения любой подсистемы (X₁,...,X_k), входящей в систему (X₁,...,X_n) называется плотность распределения этой подсистемы, вычисленная при условии, что остальные случайные величины приняли определенные значения: X_k+1=x_k+1; X_k+2=x_k+2;...,X_n =x_n.