 |
 Частные производные функций нескольких переменных называют также частными производными первого порядка или первыми частными производными.
Частные производные функций нескольких переменных называют также частными производными первого порядка или первыми частными производными.
Частными производными второго порядка от функции 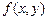 называются соответствующие частные производные от ее частных производных первого порядка, если они существуют.
называются соответствующие частные производные от ее частных производных первого порядка, если они существуют.
Для функции 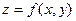 по определению имеем
по определению имеем
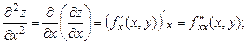
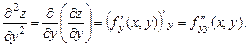
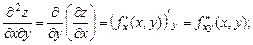
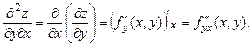
Частные производные второго порядка, взятые по различным переменным называются смешанными.
 Теорема. Если функция
Теорема. Если функция 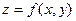 и ее смешанные производные
и ее смешанные производные 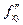 ,
,  определены в некоторой окрестности точки
определены в некоторой окрестности точки 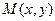 и непрерывны в этой точке, то
и непрерывны в этой точке, то
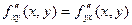 .
.
Дифференцируя частные производные второго порядка как по х, так и по у, получим частные производные третьего порядка.
Пример 8.7. Дана функция 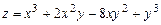 . Найти ее частные производные второго порядка.
. Найти ее частные производные второго порядка.
 Находим частные производные функции
Находим частные производные функции 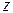 :
:
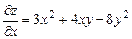 ,
, 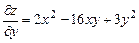 ,
,
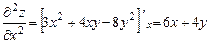 ,
, 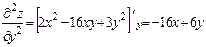 ,
,

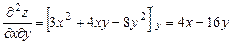 ,
, 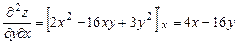 .
.
 Пример 8.8. Найти частные производные второго порядка функции
Пример 8.8. Найти частные производные второго порядка функции 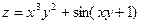 .
.
Последовательно находим
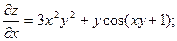
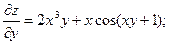
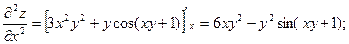
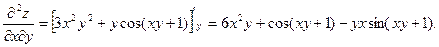
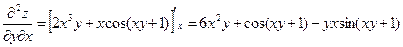
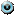

§ 5. Экстремум функции двух переменных
 Максимумом (минимумом) функции
Максимумом (минимумом) функции 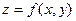 в точке M 0(x 0, y 0) называется такое ее значение
в точке M 0(x 0, y 0) называется такое ее значение 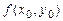 , которое больше (меньше) всех других ее значений, принимаемых в точках
, которое больше (меньше) всех других ее значений, принимаемых в точках 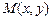 , достаточно близких к точке
, достаточно близких к точке  и отличных от нее.
и отличных от нее.

 Точки максимума и минимума называют точками экстремума, а значения функции в этих точках называются экстремальными.
Точки максимума и минимума называют точками экстремума, а значения функции в этих точках называются экстремальными.
Необходимые условия экстремума. Если дифференцируемая функция 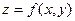 имеет экстремум в точке
имеет экстремум в точке 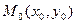 , то ее частные производные в этой точке равны нулю, т.е.
, то ее частные производные в этой точке равны нулю, т.е.
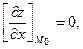
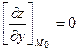 .
.

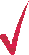 Точки, в которых
Точки, в которых 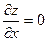 и
и 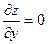 , называются стационарными точками функции
, называются стационарными точками функции 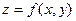 .
.
 Достаточные условия экстремума. Пусть
Достаточные условия экстремума. Пусть 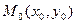 является стационарной точкой функции
является стационарной точкой функции 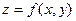 и пусть
и пусть 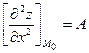 ,
, 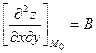 ,
, 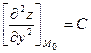 . Составим определитель
. Составим определитель 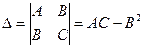 . Тогда:
. Тогда:
если 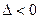 , то в стационарной точке
, то в стационарной точке 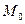 нет экстремума;
нет экстремума;

 если
если 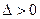 , то в точке
, то в точке 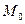 есть экстремум, причем максимум, если А < 0, минимум, если
есть экстремум, причем максимум, если А < 0, минимум, если 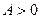 ;
;
если 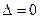 , то требуется дополнительное исследование.
, то требуется дополнительное исследование.
Пример 8.10. Исследовать на экстремум функцию 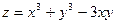 .
.
 Находим частные производные первого порядка:
Находим частные производные первого порядка: 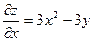 ;
; 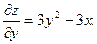 Решая систему уравнений
Решая систему уравнений

получаем две стационарные точки: 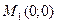 и
и 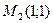 .
.
Находим частные производные второго порядка:
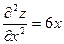 ,
, 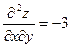 ,
, 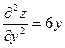 .
.
Исследуем каждую стационарную точку.
1) В точке 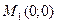 имеем:
имеем: 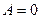 ,
, 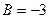 ,
, 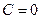 . Тогда
. Тогда 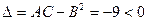 . Так как
. Так как 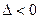 , то в этой точке нет экстремума.
, то в этой точке нет экстремума.
2) В точке 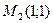 имеем:
имеем:  ,
, 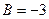 ,
, 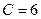 . В этом случае
. В этом случае 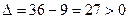 . Так как
. Так как 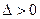 и
и 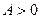 , то в этой точке функция имеет минимум
, то в этой точке функция имеет минимум

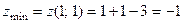 .
.
 2015-01-21
2015-01-21 276
276







