В уравнении

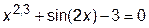
х должен быть больше нуля, в уравнении

,

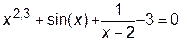кроме того, необходимо учесть, что при х =2 функция имеет разрыв и это значение аргумента следует исключить из области определения функции.

Если аналитический вид функции не известен, то проблема нахождения области определения функции становится более сложной. Здесь могут оказаться полезными сведения о физических условиях задачи. Например, при описании процесса движения воды при давлении, близком к атмосферному, ее температура ограничена пределами 0-100°С.

Для того, чтобы быть уверенным, что на некотором интервале находится корень уравнения, необходимо, чтобы на этом интервале функция меняла знак. Для поиска подобных интервалов диапазон определения функции разбивается на несколько достаточно больших интервалов одинаковой длины и затем вычисляются значения функции на их границах. Далее на интервалах, где функция меняет знаки, проводится поиск корня.

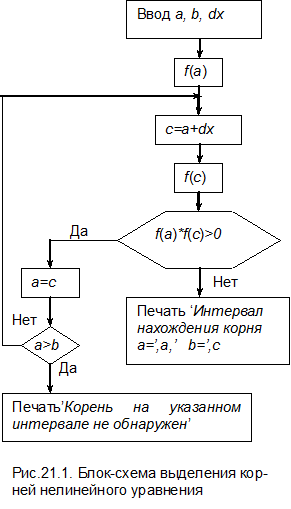
Блок-схема процедуры определения интервала приведена на рис.21.1. Сначала задается интервал [ a,b ], внутри и на границах которого существует функция f (x) и может находиться один из корней. Тут же указывается шаг поиска dx. Затем вычисляется значение функции на левой границе интервала в точке а и организуется цикл, в котором рассчитывается значение функции на расстоянии dx от точки а. Если на участке [ a,a+dx ] функция поменяла знак или приняла нулевое значение, т.е. произведение f(a)*f(b)£0, то это означает, что внутри участка [ a,a+dx ] существует корень уравнения. Если по условиям задачи требуется найти только один корень, то цикл на этом прекращается и производится вычисление корня с требуемой точностью одним из рассмотренных ниже методов. Если необходимо найти все корни уравнения, то выделение участков, содержащих корни, продолжается по аналогичной схеме.

При f (a) *f (b)>0 первоначальный интервал уменьшается на величину шага dx и проверяется, не достигла ли точка а правой границы интервала. Если этого не произошло, то цикл повторяется. Случай, когда был пройден весь интервал [ a,b ] и ни разу функция не поменяла знак, означает, что на данном интервале ни один корень уравнения не найден. При этом расчет приостанавливается и на экран компьютера выводится соответствующее сообщение.

Такая ситуация может быть обусловлена двумя причинами:

1) на интервале [ a,b ] действительно нет корней, в этом случае в зависимости от поставленной задачи необходимо согласиться с полученным сообщением или указать другой интервал поиска;

2) на интервале [ a,b ] существует четное количество корней, при этом была выбрана слишком большая ширина участков и парные корни оказались внутри одного участка. В этом случае можно повторить поиск с меньшим значением dx.

Метод половинного деления (метод дихотомии).

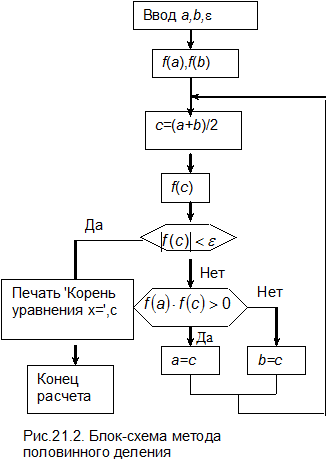
Приближенные значения корней уточняют различными итерационными методами, предполагающими последовательное приближение к искомому значению при выполнении однотипных операций. Если заранее известен интервал [ a,b ], на котором функция меняет знак, т.е. выполняется условие 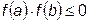, то наиболее надежным является метод половинного деления. Блок-схема метода приведена на рис. 21.2.

Для определения корня этим методом необходимо указать интервал [ a,b ], на котором функция меняет знак, и допустимую погрешность e. Затем вычисляются значения функции на границах интервала f (a) и f (b). После этого организуется цикл, в котором вычисляются середина интервала c= (a+b)/ 2 и значение функции f (c). Далее проверяется условие . При его выполнении принимается, что точка с является корнем уравнения, на экран выводится соответствующее сообщение и расчет прекращается. Если значение функции в точке с по абсолютной величине превосходит допустимую погрешность e, то из двух половин выбирается та, на которой функция меняет знак, и цикл повторяется.

Метод половинного деления прост и надежен, к корню расчет сходится при любых непрерывных функциях f (x), в том числе и недифференцируемых, при этом метод устойчив к ошибкам округления. Скорость сходимости невелика, за одну итерацию интервал неопределенности [ a,b ] сокращается вдвое, зато точность расчета гарантируется.

Недостатки метода:

1. Для начала расчета необходимо найти отрезок, на котором функция меняет знак.

2. Если на этом отрезке несколько корней, то заранее неизвестно, к какому из корней сойдется процесс, хотя к одному из них обязательно сойдется.

3. Метод не применим для решения систем уравнений.

Метод половинного деления используется, когда требуется высокая надежность счета, а скорость сходимости малосущественна.

Метод хорд.

В том случае, когда значение функции на одной границе интервала значительно ближе к нулю, чем на другой границе, более логично искать решение не на середине отрезка, а в области, расположенной ближе к первой границе.

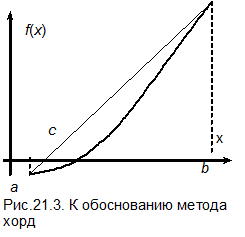
Соединив на графике значения функции на границах интервалов прямой линией, получим точку пересечения этой линии с осью абсцисс, которую будем рассматривать в качестве следующего приближения к корню уравнения. В соответствии с рис.21.3. координаты этой точки находятся из подобия треугольников:

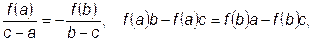откуда

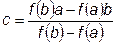. (21.3)

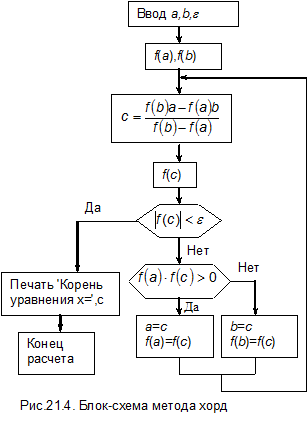
Блок-схема метода хорд приведена на рис.21.4. Она почти полностью повторяет блок-схему метода половинного деления. Отличия заключаются в расчете по иной формуле координаты точки с для дальнейшего уточнения корня и дополнительных переприсвоениях значений функций f (a)= f (c) или f (b)= f (c) при сокращении интервала неопределенности.

Метод хорд сохраняет все недостатки метода половинного деления, но при этом обычно обеспечивает более быструю сходимость.

Лекция 22. МЕТОДЫ КАСАТЕЛЬНЫХ И СЕКУЩИХ.

УСТОЙЧИВОСТЬ И БЫСТРОТА РЕШЕНИЯ РАЗЛИЧНЫХ МЕТОДОВ.

Метод Ньютона (метод касательных).

Этот метод также называется методом касательных или методом линеаризации. Если функция f (x) в области определения имеет непрерывную производную 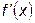, значения которой легко вычисляются, то можно значительно ускорить процесс приближения к корню.

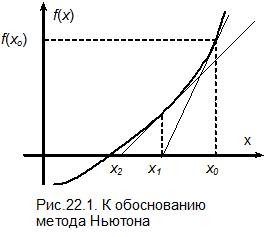
На рис.22.1. показана схема итерационных вычислений корня уравнения по методу Ньютона. Для начала расчета должны быть заданы начальная точка x₀ и допустимая погрешность e. В точке x₀ вычисляются значения функции f (x) и ее производной 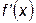. Далее функция f (x) аппроксимируется ее производной, новое приближение к корню определяется как точка пересечения касательной с осью абсцисс. Значение производной в точке x₀ равно

,

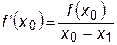откуда находится координата точки x₁:

.

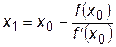Поскольку за один ход не удается найти корень уравнения, то процесс повторяется, новые приближения определяются по рекуррентной формуле

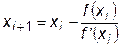(22.1)

до тех пор, пока не будет выполнено условие 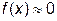или .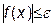

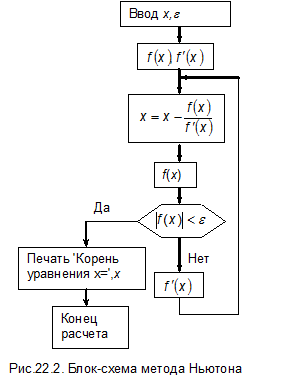
Блок-схема метода Ньютона приведена на рис. 22.2. Если нулевое приближение выбрано достаточно близко к корню, то скорость сходимости велика. К достоинствам этого метода следует отнести также то, что для начала расчета не требуется указывать диапазон, на котором функция меняет знак, а достаточно выбрать только начальную точку.

Допустим, необходимо вычислить квадратный корень из числа a, то есть решить уравнение . Запишем его в виде 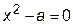. Тогда .

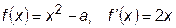Согласно (2.4) получим формулу

,

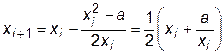которая позволяет вычислить квадратный корень, используя только операции сложения и деления. Именно эта формула запрограммирована в карманных калькуляторах.

К недостаткам метода следует отнести возможность расхождения, то есть возникновения ситуации, когда метод не в состоянии найти корни.

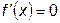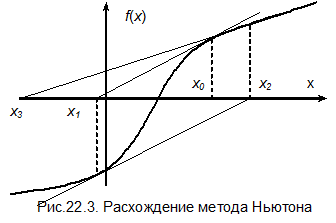
При метод не определен, при малых 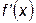или неудачном начальном приближении могут возникнуть проблемы со сходимостью, когда последующее приближение хуже предыдущего. Подобный случай показан на рис. 22.3.

Метод секущих.

В методе Ньютона необходимо вычислять производные 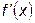. Это может потребовать много времени, может оказаться трудным или даже невозможным делом, особенно если вычисление включает, например, вычисление интеграла, решение дифференциального уравнения или если значение функции определяется результатом работы некоторого физического устройства.

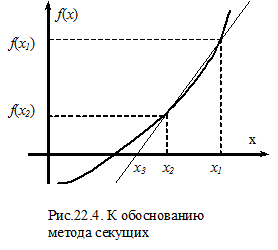
Значение производной можно вычислить приблизительно по значениям функции в двух точках x₁ и x₂, как это показано на рис.22.4.

Заменив в формуле (22.1.) производную ее приближенным значением

,

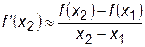получим новую формулу для определения следующего приближения к корню

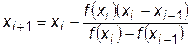(22.2)

Блок-схема метода секущих представлена на рис.22.5.

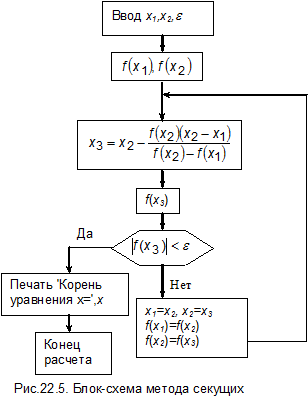
Для начала процесса надо задать две точки x₁ и x₂ и допустимую погрешность e. По сравнению с методом Ньютона из-за погрешности в определении производной для нахождения корня требуется выполнить большее количество шагов. Однако в методе секущих на каждом шаге вычисляется только одно значение функции, в то время как в методе Ньютона вычисляются значения функции и ее производной, поэтому скорость счета у них приблизительно одинакова. Недостаток метода секущих связан с тем, что в знаменателе формулы (22.2) стоит разность значений функции. Вдали от корня это несущественно, но вблизи от корня значения функции малы и очень близки. В результате этого возникает потеря значащих цифр, приводящая к «разболтке» счета, когда результаты вычисления начинают колебаться около истинного значения, не сходясь к нему. Это ограничивает точность счета.

От «разболтки» страхуются так называемым приемом Гарвика. Выбирают не очень малое e₁, ведут итерации до выполнения условия 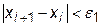и затем продолжают расчет до тех пор, пока 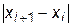убывают. Первое же возрастание обычно означает начало «разболтки», тогда расчет прекращают и последнюю итерацию не используют.

Следует отметить еще одну сторону метода секущих. Формула (22.2) идентична формуле метода хорд:

.

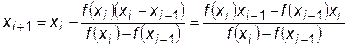Однако, метод касательных не требует указания диапазона изменения знака функции и при этом обеспечивает обычно большую скорость расчета, чем метод хорд. В свою очередь, метод хорд гарантирует нахождения корня и исключает возможность появления «разболтки», так как корень всегда находится внутри диапазона неопределенности и длина диапазона сокращается на каждом шаге.

Лекция 23. Численное интегрирование.

МЕТОДЫ ПРЯМОУГОЛЬНИКОВ, ТРАПЕЦИЙ И СИМПСОНА.

Численное значение определенного интеграла определяется по формуле

,

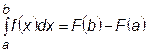где a, b – пределы интегрирования; f (x) – подинтегральная функция;

F (x) – первообразная подинтегральной функции f (x).

В практических задачах достаточно редко удается найти точное аналитическое решение, поэтому приходится прибегать к приближенному численному интегрированию. Для этого обычно заменяют функцию f (x) на близкую к ней и совпадающую с ней в ряде точек функцию j(x), для которой можно найти аналитическое решение. Поскольку на широком интервале [ a,b ] такую функцию подобрать сложно, то исходный интервал разбивают на несколько более узких и вычисляют общий интеграл как сумму интегралов по узким интервалам.

Наиболее часто функцию f (x) заменяют алгебраическим многочленом

.

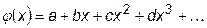Порядок многочлена определяется максимальной степенью при параметре x. Обычно ограничиваются следующими аппроксимациями:

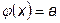- нулевая степень;

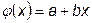- первая степень;

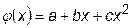- вторая степень.

Метод прямоугольников.

Определенный интеграл функции f (x) на отрезке [ a,b ] можно представить как площадь под кривой f (x), ограниченной пределами интегрирования и осью абсцисс. Разобьем отрезок [ a,b ] на n отрезков одинаковой длины

.

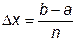В результате получим набор равноудаленных друг от друга точек 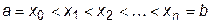. Рассмотрим один отрезок [ x_i-1,x_i ].

Для аппроксимации функции f (x) будем использовать полином нулевой степени 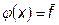, где 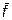- некоторая постоянная величина, ограниченная значениями
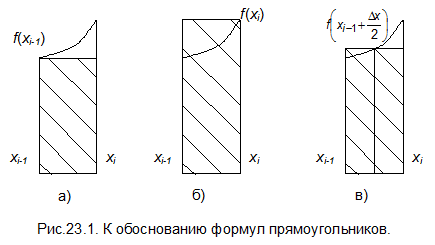
f (x_i-1) и f (x_i). Если принять, что величина 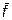равна значению f (x_i-1) на левом крае отрезка, то площадь криволинейной трапеции будет приблизительно равна площади заштрихованного на рис.23.1.а прямоугольника

.

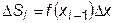Сумма площадей всех прямоугольников даст приближенное значение интеграла:

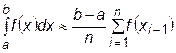. (23.1)

Это формула левых прямоугольников.

В качестве величины можно взять значение функции на правой границе отрезка f (x_i). Площадь заштрихованного прямоугольника на рис.23.1.б будет равна

,

а значение интеграла:

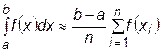. (23.2)

Это формула правых прямоугольников.

Если вычислять значение функции не на краях, а в середине интервала, то, согласно рис.23.1.в, можно ожидать увеличения точности, поскольку завышенные значения площади по сравнению с истинными на одной стороне прямоугольника компенсируются заниженными значениями на другой стороне. Площадь заштрихованного прямоугольника будет равна

,

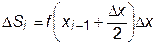а величина интеграла:

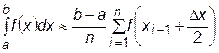. (23.3)

Это формула средних прямоугольников.

Блок-схема метода прямоугольников с заданным количеством разбиений приведена на рис. 23.2.

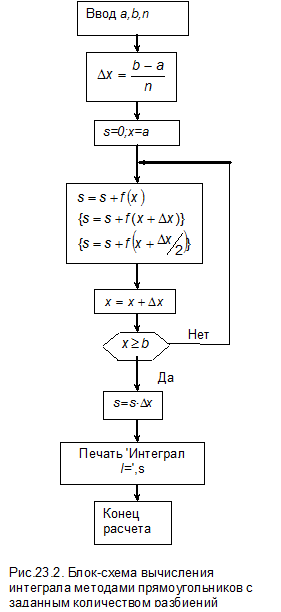
Для начала расчета задаются границы интегрирования [ a,b ] и количество подинтервалов n, на которые разбивается основной интервал. Затем в соответствии с выбранным методом интегрирования суммируются значения функции на каждом из подинтервалов. Поскольку длины подинтервалов равны между собой, то величину D x целесообразно вынести за знак суммы и умножить на эту величину окончательную сумму значений функций.

Сумма длин подинтервалов точно равна общей длине интервала интегрирования, поэтому в этом алгоритме не нужен контроль за совпадением концов последнего подинтервала и всего интервала.

В некоторых случаях более удобно задавать не количество разбиений, а шаг интегрирования D x. При этом величина D x может быть не кратной длине интервала интегрирования, поэтому на последнем шаге необходима проверка совпадения длин и при необходимости корректировка величины D x. Поскольку D x может измениться, то его нельзя выносить за знак суммы.

Блок-схема метода приведена на рис.23.3.

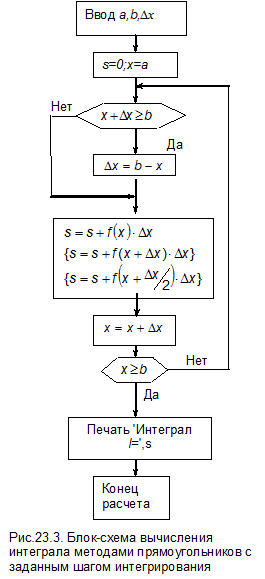
Метод трапеций.

Если для аппроксимации функции f (x) взять полином первой степени 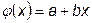и поставить условие, чтобы значения функций f (x) и j(x) совпадали на концах подинтервалов, то заштрихованная площадь на рис.3.4. будет равна

,

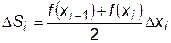а вся площадь под кривой, соответствующая значению определенного интеграла,

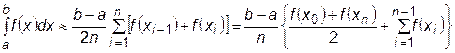. (23.4)

Это формула трапеций.

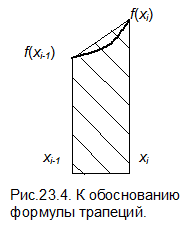
Вычисления по методу трапеций также могут быть организованы как с заданным количеством подинтервалов n, так и с заданной величиной шага D x. В блок-схемах алгоритмов на рис.23.2 и рис.23.3 изменится только узел вычисления интегральной суммы:

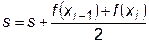
или, например, организован цикл:

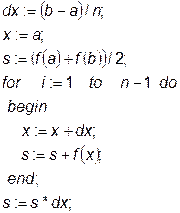
Метод трапеций удобно применять, когда подинтегральная функция задана табличным способом и известны значения функции только на границах подинтервалов.

Метод Симпсона.

Возьмем для аппроксимации функции f (x) многочлен второй степени 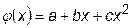. Чтобы определить коэффициенты a,b,c, необходимо на интервале аппроксимации задать три точки. Выберем шаг интегрирования D x и вычислим значения функции на концах интервала и в его середине. Обозначим, как это показано на рис.23.5, значения аргумента через x₀, x₁, x₂ и, соответственно, значения функции через f₀, f₁, f₂. Половину шага интегрирования обозначим .

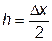Уравнение параболы, проходящей через три точки, можно записать в виде

.

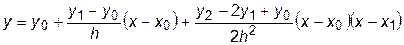Учитывая, что 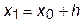, при интегрировании этой функции в пределах от x₀ до x₀+2h после преобразований получим:

.

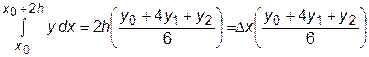Для всего интервала интегрирования будем иметь:

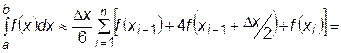
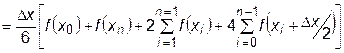, (23.5)

где .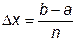

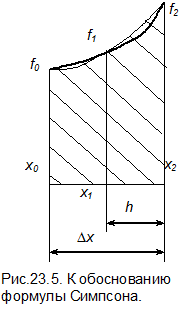
Это формула Симпсона.

Как и для рассмотренных ранее методов, вычисления интегралов по формуле Симпсона могут быть по блок-схемам рис.23.2 или рис.23.3.

Погрешность вычислений различных методов.

Точное значение определенного интеграла можно представить в виде

,

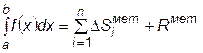где D S_i^мет - площадь элементарной фигуры (прямоугольника, прямолинейной или криволинейной трапеции), вычисленная по какому-либо методу;

R^мет – погрешность вычисления этого метода.

С увеличением количества разбиений n возрастает количество элементарных фигур, при этом ширина их уменьшается, а ломаная линия, ограничивающая площадь фигур сверху, более тесно приближается к графику функции f (x). В результате этого сумма площадей элементарных фигур становится ближе к площади криволинейной трапеции, поэтому можно считать, что при достаточно большом n эта сумма дает приближенное значение определенного интеграла.

Для оценки влияния количества разбиений или, что то же самое, длины шага интегрирования на погрешность вычислений в качестве тестовой задачи в табл.23.1. приведены результаты расчета значения определенного интеграла

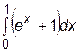
различными методами, точное значение которого до шестого знака после запятой равно 2,718282.

Таблица 23.1. Результаты численного интегрирования тестовой задачи.

Кол-во разби-ений n	Методы
Прямоугольников	трапеций	Симпсона
левых	Правых	средних
	2,000000	3,718282	2,648721	2,859141	2,718661
	2,324361	3,183502	2,700513	2,753931	2,718319
	2,512437	2,942007	2,713815	2,727222	2,718284
	2,675683	2,761597	2,718103	2,718640	2,718282
	2,675683	2,761597	2,718103	2,718640	2,718282
	2,709705	2,726888	2,718275	2,718296	2,718282
	2,716564	2,720001	2,718282	2,718282	2,718282
	2,717723	2,719141	2,718282	2,718282	2,718282
	2,718196	2,718368	2,718282	2,718282	2,718282
	2,718273	2,718290	2,718282	2,718282	2,718282

Результаты расчета показывают, что при использовании методов левых и правых прямоугольников для обеспечения даже невысокой точности вычисления приходится проводить с очень мелким шагом, приводящим к значительному увеличению продолжительности счета. При этом незначительное усовершенствование методов и переход к формулам средних прямоугольников или трапеций в несколько раз снижает погрешность вычислений, причем преимущество усовершенствования возрастает с увеличением требуемой точности расчета. По этой причине методы левых и правых прямоугольников практически не используются.

Как и следовало ожидать, наиболее точным оказался метод Симпсона. Применение трехточечной формулы позволяет проводить вычисления с более широким шагом интегрирования. При заданной точности вычисления интеграла общее количество вычислений функции меньше, несмотря на то, что по методу Симпсона в зависимости то выбранной схемы на каждом шаге производится два или три обращения к функции по сравнению с однократным обращением в методах средних прямоугольников и трапеций.

Лекция 24. АДАПТИВНЫЕ ПРОГРАММЫ ВЫБОРА ШАГА ИНТЕГРИРОВАНИЯ

Погрешность метода средних прямоугольников при вычислениях с постоянным шагом D x оценивается величиной

,

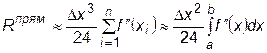где 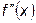- вторая производная функции f (x).

Погрешность метода трапеций приблизительно равна

.

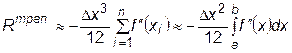В общем случае погрешность формулы средних прямоугольников примерно вдвое меньше, чем у формулы трапеций. Поэтому, если значения функции одинаково легко определяются в любых точках, то лучше вести расчет по более точной формуле средних прямоугольников. Метод трапеций употребляют в тех случаях, когда функция задана только в узлах сетки, а в середине интервала ее значения неизвестны.

Главные члены погрешностей у формул средних прямоугольников и трапеций имеют различные знаки, поэтому, если вести расчеты по обеим формулам, точное значение интеграла будет, как правило, находиться в вилке между ними. Используя это свойство, можно добиться повышения точности расчетов. Так как

, ,

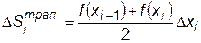то, применяя комбинированную формулу

,

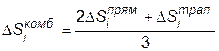сократим основные источники погрешностей. Подставляя в нее конкретные значения, получим формулу

,

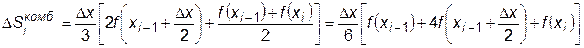соответствующую методу Симпсона, погрешность которого оценивается величиной

.

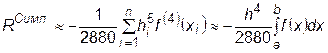В методах средних прямоугольников и трапеций уменьшение шага интегрирования D x вдвое уменьшает погрешность оценки площади элементарного прямоугольника в 8 раз, однако, общее количество этих прямоугольников увеличивается в 2 раза, поэтому общая погрешность уменьшается приблизительно в 4 раза. Коэффициент уменьшения ошибки пропорционален величине второй производной 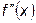и обычно не равен в точности 4, поскольку 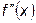не является константой и сказывается также влияние членов более высокого порядка. Однако, при реальных вычислениях с функциями, имеющими непрерывные ограниченные вторые производные, можно ожидать, что удвоение числа элементарных отрезков для любой формулы – средних прямоугольников или трапеций – приблизительно учетверяет точность.

Если в методе Симпсона уменьшить шаг D x в два раза, то каждое Dх⁵ уменьшится в 32 раза, при этом общее количество элементарных фигур возрастет в 2 раза. Погрешность в целом уменьшится приблизительно в 16 раз.

При выборе количества разбиений n или величины шага D x заранее неизвестно, какова будет погрешность вычисления интеграла. Кроме того, точное значение интеграла также неизвестно и сравнить полученное значение с точным нельзя.

Для оценки точности вычисления сравнивают два последовательных приближения к результату. Сначала задают некоторое начальное n₁, для которого вычисляют приближенное значение S₁. Затем число участков удваивают, n₁ =2 n₁, соответственно длины участков сокращаются вдвое, 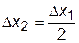. Далее вычисляют новую сумму площадей более узких фигур S₂. Она точнее приближает искомое значение интеграла. Разность 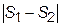сравнивают с наперед заданным малым положительным числом e. При 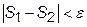считают, что S₂ можно принять за приближенное значение интеграла, полученное с заданной точностью e. В противном случае процесс деления отрезков повторяют, принимая n₃=2n₂, вычисляют S₃ и сравнивают 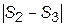с e.

Для непрерывных функций условие 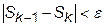должно наступить обязательно, если e>e_маш. Следует отметить, что выполнение условия 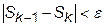в общем случае не означает, что погрешность вычисления интеграла меньше величины e. Здесь сравнивается окончательное значение S_k не с точным значением, а с вычисленным ранее при более крупном шаге интегрирования. Тем не менее, для многих функций такая оценка величины погрешности является достаточной.

При численном интегрировании величина погрешности зависит не только от используемого метода, но и от вида интегрируемой функции. Основным способом уменьшения погрешности вычисления интеграла является уменьшение ширины элементарного отрезка Dх, т.е. увеличение количества разбиений. Однако это приводит к увеличению объема вычислений и соответственно к увеличению продолжительности счета.

Вместе с тем влияние ширины отрезка Dх на точность расчета может быть неодинаковым на разных участках интегрирования. Если функция на некотором участке изменяется мало или ее вид близок к виду аппроксимирующей функции j(х), то для обеспечения требуемой точности целесообразно проводить вычисления с более крупным шагом. Там, где функция изменяется более быстро, целесообразно уменьшать шаг интегрирования.

Для обеспечения выбора приемлемого шага интегрирования на участке в зависимости от выбора типа метода интегрирования и поведения подинтегральной функции применяются адаптивные программы, построенные на алгоритмах с одной или двумя функциями, автоматически определяющими величину шага.

Пользователь подобной программы указывает конечный интервал [ a,b ] и допустимую погрешность e. Программа пытается вычислить величину S, такую, что

.

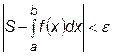В процессе вычислений интервал [ a,b ] разбивается на подинтервалы [ x_i-1,x_i ]. В большинстве программ новый подинтервал получается делением пополам подинтервала, полученного на более раннем этапе вычисления. Реальное число подинтервалов и их длина зависят от функции f(x) и требуемой точности e.

Типичная схема применяет к подинтервалу две различные формулы. Например, схемы, основанные на формуле Симпсона, используют основную формулу с двумя элементарными отрезками

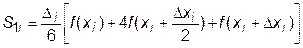
и составную формулу с четырьмя элементарными отрезками

.

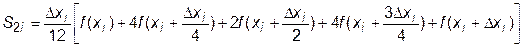Выражения S_1i и S_2i являются приближениями к величине интеграла

.

Основная идея адаптивного метода состоит в сравнении двух приближений S_1i и S_2i и получении при этом оценки их точности. Если точность приемлема, то одно из чисел принимается в качестве значения интеграла по данному подинтервалу. Если точность недостаточна, то подинтервал делится на две или более частей и процесс повторяется для меньших подинтервалов. Если точность значительно меньше требуемой, то на следующем шаге величина подинтервала увеличивается.

Сокращение общего количества вычислений может быть достигнуто также за счет того, что две формулы для расчета S_1i и S_2i используют значения подинтегральной функции в нескольких общих точках. Например, для формулы Симпсона S_2i требует вычисления в пяти точках, три из которых используются при расчете S_1i, и поэтому достаточно вычислить только два новых значения функции f(x).

Для формулы Симпсона сокращение интервала вдвое увеличивает точность вычисления приблизительно в 16 раз.

.

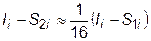Выразим отсюда неизвестную величину I_i – S_2i:

.

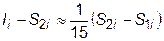Проводя подобные вычисления для формул прямоугольников или трапеций, получим оценку погрешности

.

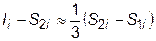Разность между истинным значением и результатом вычисления с уменьшенным вдвое шагом оказывается меньше, чем разность между результатами расчета с первоначальным и половинным шагом. Поэтому, если на каждом шаге обеспечить выполнение условия

,

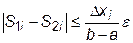то при суммировании всех интервалов будем иметь

.

На рис. 24.1 приведена блок-схема адаптивного алгоритма вычисления определенного интеграла методом средних прямоугольников. В начале программы в качестве шага интегрирования выбирается длина всего диапазона интегрирования. Далее по двум формулам с целым и половинными шагами рассчитываются значения интеграла на участке шириной D x.

При обеспечении требуемой точности расчета полученное значение S_2i суммируется с вычисленными ранее на предыдущих интервалах и делается следующий шаг.

Если точность расчета заметно (в приведенной схеме в 20 раз) превышает требуемую, длина шага увеличивается в 1,87 раза. В том случае, если погрешность расчета оказывается чрезмерной, длина шага уменьшается вдвое.

Коэффициенты увеличения и уменьшения шага выбраны не кратными друг другу для более гибкого изменения длины шага интегрирования. В зависимости от вида подинтегральной функции и желания программиста эти величины могут быть выбраны несколько иными.

Лекция 25. Решение системы линейных уравнений МЕТОДОМ ГАУССА

В инженерных расчетах довольно часто приходится решать системы линейных уравнений. В общем случае система имеет вид

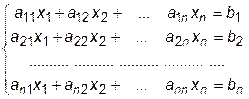(25.1)

Здесь х₁, х₂, …,х_n – неизвестные параметры, значения которых необходимо найти; а₁₁, а₁₂, …, а_1n, а₂₁, …, а_2n, …, а_nn – известные коэффициенты при неизвестных параметрах х₁, х₂, …,х_п. Первый индекс коэффициента означает номер строки (номер уравнения в системе), второй индекс – номер неизвестного параметра, при котором стоит данный коэффициент; b₁, … b_n – свободные члены в уравнениях, индекс означает номер уравнения.

Обычно число уравнений равно числу неизвестных. В этом случае коэффициенты при неизвестных и свободные члены образуют матрицу размером n ´ n +1. Здесь целесообразно свободные члены обозначить как элементы матрицы с индексами i,n+1 (а_i,n+1). Параметр i принимает значения от 1 до n.

Для того, чтобы система имела единственное решение, входящие в нее n уравнений должны быть линейно независимыми, то есть никакое уравнение не может быть линейной комбинацией других уравнений. Необходимым и достаточным условием существования единственного решения является неравенство нулю определителя матрицы коэффициентов.

Алгоритмы решения задач такого типа делятся на прямые и итерационные. Прямые методы дают решения за конечное число действий. Для систем порядка n <200 применяются практически только прямые методы. Итерационные методы выгодны для систем со слабо заполненной матрицей большого порядка n @10³-10⁵.