Изменение характеристик потока жидкости, таких как скорость, направление движения, расход за счет слияния или разделения потоков и т.п., приводит к потерям энергии (напора, давления). Поскольку указанные изменения происходят на коротком участке, то такие потери называют местными. Элементы трубопроводов, в которых наблюдаются местные потери энергии, называют местными сопротивлениями. К ним относят: клапаны, краны, всевозможные регуляторы расхода и давления, золотники, колена, тройники, фильтры и т.п.
Аналитическое определение местных потерь энергии возможно только в некоторых простейших случаях. Для практических расчетов используют формулу Дарси
 , (1.51)
, (1.51)
где 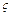 – коэффициент местных потерь, определяемый экспериментальным путем.
– коэффициент местных потерь, определяемый экспериментальным путем.
Потери энергии при внезапном расширении потока
Примером аналитического определения местных потерь энергии является задача о внезапном расширении движущейся жидкости.
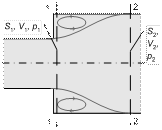 Рассмотрим поток, движущийся со скоростью V 1 в круглой цилиндрической трубе, площадь поперечного сечения которой равна S 1. При внезапном увеличении площади трубы до величины S 2 струя жидкости постепенно заполнит все поперечное сечение большей трубы, и на некотором расстоянии от места расширения установится течение со скоростью V 2<V1.
Рассмотрим поток, движущийся со скоростью V 1 в круглой цилиндрической трубе, площадь поперечного сечения которой равна S 1. При внезапном увеличении площади трубы до величины S 2 струя жидкости постепенно заполнит все поперечное сечение большей трубы, и на некотором расстоянии от места расширения установится течение со скоростью V 2<V1.
|
|
|
Для определения разности давлений в сечениях 1-1 и 2-2 воспользуемся уравнением изменения количества движения (уравнением импульса), согласно которому изменение количества движения потока во времени равно главному вектору приложенных к нему внешних сил. Изменение количества движения за единицу времени можно представить следующим выражением
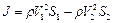 .
.
Внешней силой, приложенной к выделенному объему, является сила, возникающая в результате разности давлений, действующих на торцевые поверхности
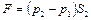 .
.
Приравнивая эти выражения, получим
 .
.
Принимая во внимание, что массовый расход жидкости постоянен, 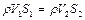 , последнее уравнение преобразуется к виду
, последнее уравнение преобразуется к виду
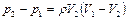 .
.
При внезапном расширении идеальной жидкости, изменение давления между рассматриваемыми сечениями определяется на основании уравнения Бернулли
 .
.
Разность этих уравнений дает потерю энергии, обусловленную вязкостью жидкости, которая превращается в теплоту
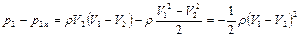 .
.
Полученное выражение получило название формулыБорда. Ее можно преобразовать к виду, соответствующему уравнению Дарси,
|
|
|
 .
.
Первый сомножитель в правой части уравнения представляет собой коэффициент местного сопротивления при внезапном расширении, который, с учетом уравнения неразрывности ( ), можно представить в следующем виде
), можно представить в следующем виде
 .
.
 2015-01-30
2015-01-30 741
741








