Тема 1. Теплопроводность при нагревании (охлаждении) тел

Нестационарный теплообмен встречается во многих практических ситуациях. Например, чтобы получить требуемые физические свойства, металлы нагревают и охлаждают. В двигателях внутреннего сгорания происходят переходные процессы при запуске, а также более быстрые периодические нестационарные процессы в каждом такте термодинамического цикла. При сварке деталей их температура изменяется во времени и по координатам. В общем случае нестационарные задачи решать труднее, чем стационарные.

Цель решения нестационарной задачи состоит в определении температурного поля тела и количества полученной или отданной телом теплоты по истечении определенного периода времени.

Рассмотрим наиболее распространенную задачу нестационарной теплопроводности одноразовое охлаждение (нагревание) тела.

Охлаждение (нагревание) бесконечной пластины

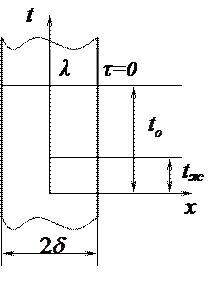Постановка задачи. Пусть имеется пластина, размер которой вдоль оси х равен 2. Размеры пластины в направлении осей y и z неограниченны, т.е. температура пластины изменяется только в направлении оси х. Пластина помещается в среду, температура которой = const. В начальный момент времени (t = 0) температура в пластине распределена равномерно и равна 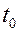, (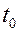>), т.е. рассматриваем процесс охлаждения пластины. Все рассуждения и полученный результат будут верны и для процесса нагревания. Теплообмен с обеих поверхностей пластины одинаковый, коэффициент теплоотдачи a = const. В этом случае температурное поле будет симметричным относительно середины пластины. Теплоемкость и коэффициент теплопроводности материала пластины не зависят от температуры. Необходимо найти закон распределения температуры по толщине пластины и количество теплоты, отводимой с поверхности пластины, за любой промежуток времени.

Обозначим избыточную температуру в любой точке тела в произвольный момент времени через 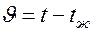. При t = 0 .

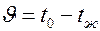Для нахождения закона распределения температуры по толщине пластины в любой момент времени запишем дифференциальное уравнение теплопроводности, учитывая, что 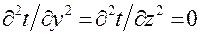. Согласно условию задачи уравнение теплопроводности будет иметь вид

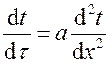или .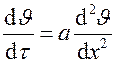

Для решения этого уравнения воспользуемся методом разделения переменных [8]. Представим искомую функцию 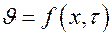в виде произведения T (t) и L (x):

.

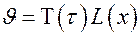Первый множитель зависит только от времени, а второй – только от координаты.

Дифференцируя выражение, найдем 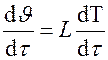; ; 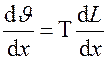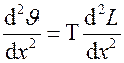. Подставим эти значения в решение, получим

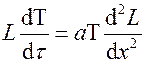или .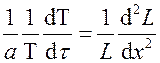

Левая часть этого уравнения есть функция от времени (t), а правая – от координаты (x). Значит, обе части должны быть равны некоторой постоянной величине, которую обозначим через (минус ).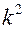

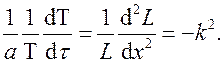
Тогда

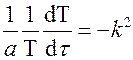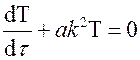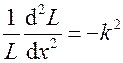или ,

или .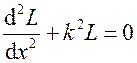

Это система обыкновенных дифференциальных уравнений, общие решения которых известны:

.

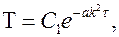
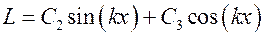Общее решение будет иметь вид

.

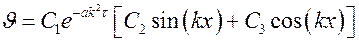Для нахождения частного решения необходимо

определить постоянные интегрирования (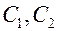 и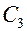), а также k. Для

этого запишем начальные и граничные условия: при t = 0 ;

при x = 0 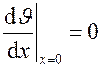; при x = ± d 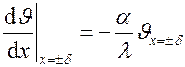. Решая эту задачу (подробное решение можно посмотреть в [1]), получаем уравнение температурного поля в бесконечной пластине в виде

,

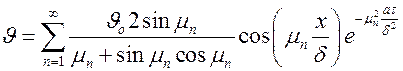где 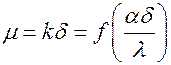. Запишем формулу в безразмерной форме. Обозначим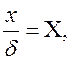 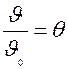, , 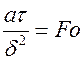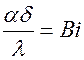– соответственно безразмерные координата, температура, безразмерные числа Фурье и Био.

.

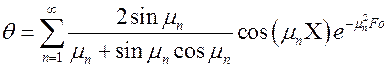Анализ формулы показывает, что чем больше номер ряда, тем меньшую долю вносит член в общую сумму ряда, т.е. ряд быстро сходится, особенно при 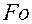³ 0,3. При этом распределение температуры достаточно точно описывается первым членом ряда:

.

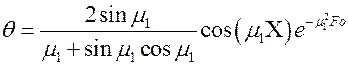Пользование полученным уравнением на практике затруднительно. Поэтому с помощью формулы построены графики (номограммы)

= ¦(X, Fо, Bi), использование которых сводит расчеты к довольно простым операциям. Для практики часто бывает достаточно контролировать температуру тела в его центре или на поверхности и по изменению ее величины судить о процессе нагревания (охлаждения).

Безразмерную температуру в центре пластины (x = 0, X = 0) можно определить по формуле

,

а на поверхности пластины (x = d, X = 1)

.

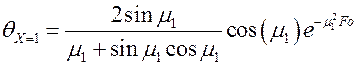Первые сомножители в этих выражениях зависят только от Bi.

Обозначим их следующим образом:

,

,

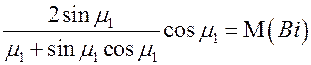тогда

,

.

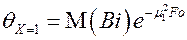Прологарифмируем последние два выражения

,

.

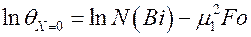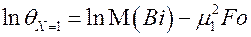Графически эти зависимости представлены на номограммах. Пользуясь этими номограммами, можно легко найти температуру в центре и на поверхности бесконечной пластины (такие же номограммы имеются и для бесконечного цилиндра и шара) в любой момент времени. Для этого необходимо рассчитать безразмерные числа Bi и Fо и отложить их значения на соответствующей номограмме. Точка пересечения даст величину безразмерной температуры 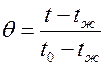. Зная , можно вычислить размерную температуру .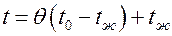

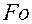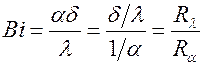Физический смысл безразмерных чисел и . характеризует соотношение между термическими сопротивлениями теплопроводности и теплоотдачи. 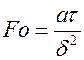характеризует безразмерное время.