При тех же условиях (1) найдем реакцию (N1) направляющих в момент времени
t1 = 2 с. Опять рассмотрим механическую систему, состоящую из плиты и груза D, и изобразим действующие на нее внешние силы 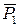 ,
, 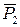 и реакцию
и реакцию 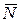 (см. рис. 7.7). Для определения N1, воспользуемся теоремой о движении центра масс системы и составим дифференциальное уравнение его движения в проекции на ось y:
(см. рис. 7.7). Для определения N1, воспользуемся теоремой о движении центра масс системы и составим дифференциальное уравнение его движения в проекции на ось y:
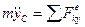 или
или 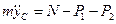 , (9)
, (9)
где т – масса системы; Р1 = m1g; Р2 = m2g. Из формулы, определяющей ординату (уС)центра масс системы, следует, что для рассматриваемой системы: туС = т1уС1 + т2уD, где (как видноиз рис. 7.7) уС1 = h, yD = 2h – l cos φ. Тогда, используя равенство (7), получим:
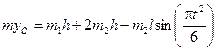 .
.
Вычисляя производные и учитывая, что h = const, получим:
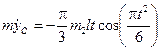 ;
;
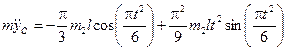 .
.
Подставив найденное значение 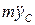 в равенство (9), найдем зависимость N от t и из нее, полагая t = t1 = 2 с, определим искомую величину N1.
в равенство (9), найдем зависимость N от t и из нее, полагая t = t1 = 2 с, определим искомую величину N1.
Ответ: N1 = 197,3 H.
4. Определение угловой скорости ω
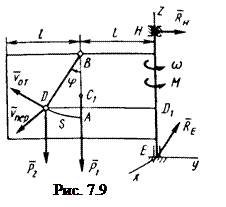
Плита вращается вокруг оси z, лежащей в плоскости плиты (рис. 7.9), и в момент времени t0 = 0, когда угловая скорость плиты равна ω0, на нее начинает действовать вращающий момент М.
|
|
|
Дано: дополнительно к условиям (1): ω0 = 5 с-1; М = kt, где k = 10 Н·м/с.
Определить: ω = f (t) – зависимость угловой скорости плиты от времени.
 Решение
Решение
Рассмотрим механическую систему, состоящую из плиты и груза D. Изобразим действующие на нее внешние силы: силы тяжести 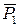 ,
, 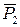 , реакции
, реакции 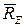 и
и 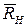 подпятника и подшипника и вращающий момент М. Для определения ω применим теорему об изменении кинетического момента системы относительно оси z. Предварительно заметим, что, так как силы
подпятника и подшипника и вращающий момент М. Для определения ω применим теорему об изменении кинетического момента системы относительно оси z. Предварительно заметим, что, так как силы 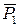 и
и 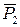 параллельны оси z, а реакции
параллельны оси z, а реакции 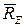 и
и 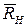 эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда
эту ось пересекают, то их моменты относительно оси z равны нулю. Тогда 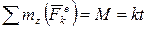 , и согласно теореме имеем:
, и согласно теореме имеем:
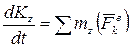 или
или 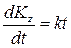 . (10)
. (10)
Умножая обе части этого уравнения на dt и интегрируя, получим:
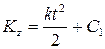 . (11)
. (11)
Для рассматриваемой механической системы
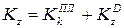 , (12)
, (12)
где 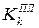 и
и 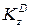 – кинетические моменты относительно оси z плиты и груза D соответственно. Поскольку плита вращается вокруг оси z, то
– кинетические моменты относительно оси z плиты и груза D соответственно. Поскольку плита вращается вокруг оси z, то
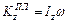 , где
, где 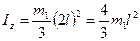 . (13)
. (13)
Для определения 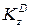 рассмотрим движение груза как сложное, считая его движение по отношению к плите относительным, а вращение плиты вокруг оси z – переносным движением. Тогда
рассмотрим движение груза как сложное, считая его движение по отношению к плите относительным, а вращение плиты вокруг оси z – переносным движением. Тогда 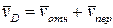 , и по теореме Вариньона имеем:
, и по теореме Вариньона имеем:
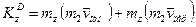 . (14)
. (14)
Но вектор 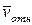 лежит в одной плоскости с осью z и, следовательно,
лежит в одной плоскости с осью z и, следовательно, 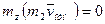 . Вектор
. Вектор 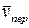 направлен перпендикулярно плите (как ось х, если ось у в плоскости плиты); по модулю
направлен перпендикулярно плите (как ось х, если ось у в плоскости плиты); по модулю 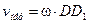 . Тогда
. Тогда 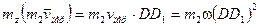 . Ноиз рис. 7.9 видно, что
. Ноиз рис. 7.9 видно, что 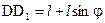 . Взяв значение sin φ из формулы (3) и подставив все найденные величины в равенство (14), получим:
. Взяв значение sin φ из формулы (3) и подставив все найденные величины в равенство (14), получим:
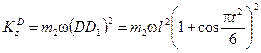 . (15)
. (15)
Зная 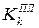 и
и 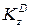 (формулы (13) и (15)), найдем из равенства (12) значение
(формулы (13) и (15)), найдем из равенства (12) значение 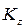 ; тогда уравнение (11) примет вид:
; тогда уравнение (11) примет вид:
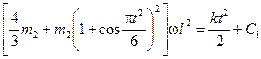
или при числовых значениях задачи
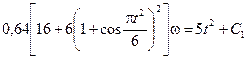 . (16)
. (16)
Постоянную интегрирования определим по начальным условиям: при t = 0
ω = ω0 = 5 с-1; получим С1 = 128. При этом значении С1 из уравнения (16) находим искомую зависимость ω от t.
|
|
|
Ответ: 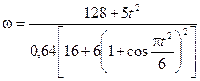 .
.
Примечание. Из полученного результата можно найти и значение ω1, при t = t1. Но если по условиям задачи одновременно М = 0, то уравнение (10) дает Kz = const, и тогда проще не искать зависимость ω от t в общем виде, а сначала определить положение груза D при t = 0 (т.е. угол φ0) и вычислить значение Кz0 при φ = φ0, и ω=ω0 с помощью равенств, аналогичных (11) – (15); затем определить положение груза при t = t1, (угол φ1) и тем же путем найти Кz1 при φ = φ1, и ω=ω1.
Так, в рассмотренном примере при t = 0 будет φ0 = π /2 и DD1 = 2 l (рис. 7.9), а при
t = t1 = 2 с будет φ1 = – π /6 и DD1 = l /2. Тогда
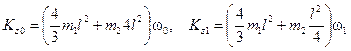 .
.
Значение ω1 находится из равенства: 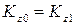 .
.
 2015-01-30
2015-01-30 775
775








