Метод хорд. где функция f(x)определена и непрерывна на интервале [a, b] и выполняется соотношение f(a)·f(b) < 0

Пусть дано уравнение

f (x) = 0, (11.4)

где функция f (x)определена и непрерывна на интервале [ a, b ] и выполняется соотношение f (a) ·f (b) < 0.

Пусть для определенности f (a) < 0, f (b) > 0. Тогда вместо того, чтобы делить отрезок [ a, b ] пополам, более естественно разделить его в отношении
- f (a) :f (b). При этом новое значение корня определяется из соотношения

x₁ = a + h₁, (11.5)

где

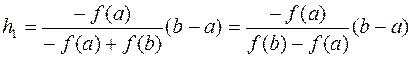. (11.6)

Далее этот прием применяем к одному из отрезков[ a, x₁ ] или [ x₁, b ], на концах которого функция f (x) имеет противоположные знаки. Аналогично находим второе приближение x₂ и т.д. (см. рис. 4.2.).

Геометрически этот способ эквивалентен замене кривой y = f(x) хордой, проходящей через точки А (a, f (a)) и B (b, f (b)).

Рис. 4.2. Уточнение корня уравнения методом хорд

Действительно, уравнение хорды АВ имеет вид

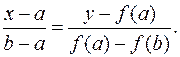(11.7)

Учитывая, что при х = х₁ => y = 0, получим

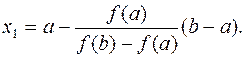(11.8)

Полагая, что на отрезке [ a, b ] вторая производная f'' ( x ) сохраняет постоянный знак, метод хорд сводится к двум различным вариантам:

1. Из рис. 11.2, a видно, что неподвижна точка а, а точка b приближается к ξ, то есть

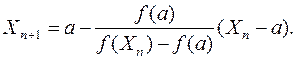(11.9)

Преобразовав выражение (11.9), окончательно получим

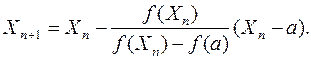(11.10)

2. Из рис. 11.2, b видно,что точка b остается неподвижной, а точка а приближается к ξ, тогда вычислительная формула примет вид

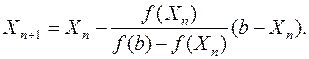(4.11)

Таким образом, для вычисления корня уравнения имеем две различные вычислительные формулы (4.10) и (4.11).

Какую точку брать за неподвижную?

Рекомендуется в качестве неподвижной выбирать ту точку, в которой выполняется соотношение

f (x) ·f” (x) > 0. (11.12)