Теоретическое обоснование работы. Исследуем вынужденные колебания тела (материальной точ­ки ) массы т , подвешенного на пружине с коэффициентом жест­кости с (рис

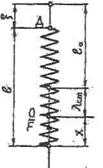
Исследуем вынужденные колебания тела (материальной точ­ки) массы т, подвешенного на пружине с коэффициентом жест­кости с (рис. 9.1).

Пусть верхний конец Д пружины совершает вертикальные колебания по закону:

ξ = r sinpt (9.1)

где р - частота вынужденных колебаний;

r - амплитуда вынужденных колебаний.

Поместим начало координат О в положение статического равновесия груза и направим ось ОХ по вертикали вниз. Если обозначить длину недеформированной пружины l₀, то ее длина в произвольный момент времени будет

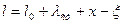
а удлинение

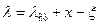
Тогда действующая на тело сила упругости

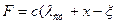
Рис. 9.1. Схема к исследованию вынужденных колебаний материальной точки.

Составляя дифференциальное уравнение движения груза, бу­дем иметь:

тх = -с(λ_с+ x-ξ)+mg

Отсюда, учитывая то, что mg = с λ_с вводя обозначение с/т = к², после преобразований получим:

x + k²x~ кξ,

Или с учетом (9.1)

х + к²х = k²r sin pt

Далее, вводя обозначение к² r = р₀, будем иметь

x + k²x = p₀ sin pt

Решение данного дифференциального уравнения будет иметь окончательный вид:

х = A sin (kt + а)+ ₂ ^Ро ₂ sin pt _? (9.2)

где Ana- постоянные интегрирования, определяемые по начальным условиям.

Решение (9.2) показывает, что колебания тела слагаются из собственных колебаний с амплитудой А, частотой к и колебаний с амплитудой Б = р₀ / (к² - р²), частотой р, называемых вынуж­денными колебаниями.

Практически, благодаря неизбежному наличию тех или иных сопротивлений, собственные колебания будут постепенно зату­хать. Поэтому в уравнении (9.2) основное место будет иметь со­ставляющая вынужденных колебаний. Амплитуду этих колеба­ний можно представить в виде:

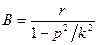
Как видим, амплитуда Б зависит от отношения частоты p воз­мущающей силы к частоте собственных колебаний к. Если р«к (верхний конец пружины колеблется очень медленно), то В≈r. При р = к наступит резонанс и размах колебаний сильно возрастает. Если частота р станет больше к, то амплитуда колебаний также уменьшается. Наконец, когда р»к амплитуда В≈0.

Для графического представления данной зависимости введем обозначения:

z=plk (9. 4)

η= Blr (9. 5)

Безразмерный коэффициент ц называем коэффициентом ди­намичности. С учетом обозначений (9.4) и (9.5) выражение (9.3) примет вид:

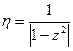(9.6)

Частоту собственных колебаний к тела в выражении (9.4) можно найти из принятого обозначения к² = с/т с учетом равен­ства mg = cλ_с. т.е. по формуле:

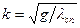■ (9.7)

Частота собственных колебаний к тела может быть найдена также, зная период колебаний Т, по истечении которого фаза ко­лебаний изменится на 2л, т. е. из соотношения:

к = 2π/Т (9.8)