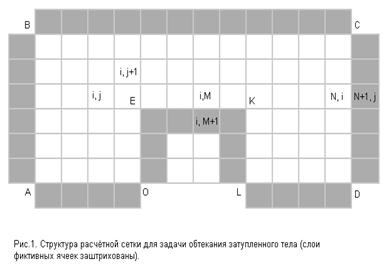
Рассмотрим в качестве примера задачу о расчете течения около затупленного тела. Область, в которой проводятся вычисления, а также расчетная сетка показаны на Рис.1(первый и последний рисунок).
Граничные условия ставились следующим образом: на левой границе АВ использовались условия в набегающем потоке газа, на теле OEKL – обычные условия на твердой стенке (условия непротекания или прилипания), на верхней ВС и правой СД открытых границах области проводилась экстраполяция параметров течения за рассматриваемую область.
Вдоль всех границ вводятся слои фиктивных ячеек, куда и засылаются соответствующие параметры из смежных ячеек потока.
 При этом следует различать два рода границ: твёрдая стенка и открытая граница расчетной области. В первом случае, например при условии непротекания, нормальная к стенке компонента скорости меняет знак в слое фиктивных ячеек, а остальные параметры потока сносятся туда без изменения. Возможен также иной тип граничных условий на стенке: течение без проскальзывания. В этом случае обе компоненты скорости меняют знак (условие прилипания).
При этом следует различать два рода границ: твёрдая стенка и открытая граница расчетной области. В первом случае, например при условии непротекания, нормальная к стенке компонента скорости меняет знак в слое фиктивных ячеек, а остальные параметры потока сносятся туда без изменения. Возможен также иной тип граничных условий на стенке: течение без проскальзывания. В этом случае обе компоненты скорости меняют знак (условие прилипания).
|
|
|
Пусть одной из прилегающих сверху к телу ячеек отвечают индексы (i, M), а соответствующей ей фиктивной ячейке внутри тела – индексы (i, M+1) (Рис. 1.). Тогда при указанной выше трактовке граничные условия непротекания на теле запишутся так:
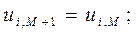 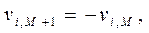
| (1) |
а условия прилипания –
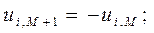 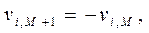
| (2) |
Через открытые границы жидкость может втекать или вытекать из области, и здесь должны быть обеспечены некоторые условия непрерывности движения. Пусть, например, жидкость втекает в прямоугольную область с левой стороны, тогда здесь и задаются параметры набегающего потока. На остальных открытых границах проводится экстраполяция параметров потока изнутри, т.е. в фиктивный слой переносятся значения параметров из ближайшего (к границе) слоя.
Рассмотрим случай, когда жидкость вытекает справа из сетки длиной в N ячеек. Наиболее естественно представить вытекающий поток однородным. В простейшем случае условия на слое j в фиктивной ячейке (N+1, j) должны бать такими же, как и в самой ячейке (N, j) (Рис. 1.). Таким образом, в конце эйлерова этапа каждого цикла вычислений полагаем:
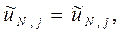 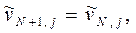 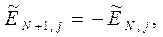
| (3) |
и в конце заключительного этапа имеем:
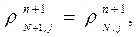 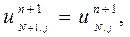 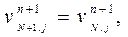 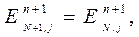
| (4) |
 2015-01-07
2015-01-07 1341
1341








