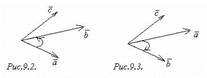
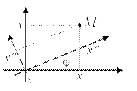
Три некомпланарных вектора A, B, C, взятых в указанном порядке называют тройкой векторов. Пусть векторы А, B и С отложены из одной точки. Будем смотреть с конца вектора С на плоскость, в которой лежат векторы А и В. Если кратчайший поворот от А к В совершается против часовой стрелки, то тройка векторов A, B, C называется правой тройкой (рис.9.2). Если же указанный поворот совершается по часовой стрелке, то тройка векторов A, B, C называется левой (рис.9.3).
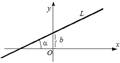
2. 1)y = kx + b, где k − угловой коэффициент, 2) y − y 0= k (x − x 0) - уравнение прямой, которая проходит
b − отрезок, который прямая отсекает на оси OY. через заданную точку P (x 0, y 0) под заданным углом α к оси OX (k = tgα).
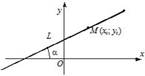
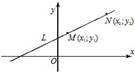
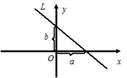
3) x − x 1 x 2− x 1= y − y 1 y 2− y 1 - уравнение прямой, которая 4) xa + yb =1 - уравнение прямой в отрезках на осях,
проходит через две точки M (x 1, y 1) и N (x 2, y 2). где a и b − величины отрезков, которые прямая отсекает на осях координат.
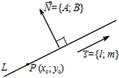
5) x − x 0 l = y − y 0 m - каноническое уравнение прямой, 6) A (x − x 0)+ B (y − y 0)=0 - уравнение прямой L,
где S ¯¯=(l, m)− направляющий вектор прямой, то есть вектор которая проходит через точку M (x 0, y 0) перпендикулярно вектору N ¯¯¯=(A, B).
|
|
|
параллельный прямой (S ¯¯∥ L), точка P (x 0, y 0)∈ L. Вектор N ¯¯¯ называется нормальным вектором прямой.
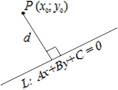
7) Ax + By + C =0− общее уравнение прямой L, 8) x cos α + y cos β − p =0− нормальное уравнение прямой,
где N ¯¯¯=(A, B)− нормальный вектор прямой L. где cos α и cos β − направляющие косинусы нормального вектора n,
направленного из начала координат в сторону прямой,
а p >0− расстояние от начала координат до прямой.
Общее уравнение прямой приводится к нормальному,
путем умножения на нормирующий множитель μ =− sgnCA 2+ B 2√.
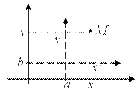
3. Преобразование декартовой прямоугольной системы координат.
Параллельный перенос: 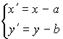 , ,
| 
|
где координаты точки Mв старой системе координат: 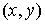 ;
;
координаты точки M в новой системе координат: 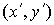 ;
;
координаты нового начала координат: 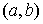 .
.
Поворот: 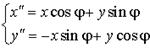 , ,
| 
|
где координаты точки M в старой системе координат: 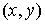 ;
;
координаты точки M в новой системе координат: 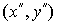 ;
;
угол поворота: j.
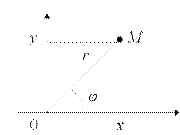
Переход от декартовых прямоугольных координат 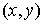 к полярным координатам к полярным координатам 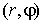 и обратно. и обратно. 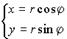 ; ;
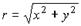 ; ; 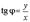 ; ; 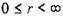 ; ; 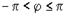
| 
|
4. Определение. Любое уравнение вида, связывающее координаты x, y, z любой точки некоторой поверхности является уравнением этой поверхности.
Определение. Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0,
где А, В, С – координаты вектора N=Aj+Bj+Cj -вектор нормали к плоскости.
Возможны следующие частные случаи:
А = 0 – плоскость параллельна оси Ох
В = 0 – плоскость параллельна оси Оу
|
|
|
С = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
А = В = 0 – плоскость параллельна плоскости хОу
А = С = 0 – плоскость параллельна плоскости хОz
В = С = 0 – плоскость параллельна плоскости yOz
А = D = 0 – плоскость проходит через ось Ох
В = D = 0 – плоскость проходит через ось Оу
С = D = 0 – плоскость проходит через ось Oz
А = В = D = 0 – плоскость совпадает с плоскостью хОу
А = С = D = 0 – плоскость совпадает с плоскостью xOz
В = С = D = 0 – плоскость совпадает с плоскостью yOz
Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат.
Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы M 1 M 2,M 1 M 3,M 1 M были компланарны, т.е. (M 1 M 2,M 1 M 3,M 1 M) = 0
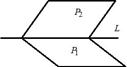
5. 1) { A 1 x + B 1 y + C 1 z + D 1=0(P 1) A 2 x + B 2 y + C 2 z + D 2=0(P 2)− общее уравнение прямой L в пространстве, как линии пересечения двух плоскостей P 1 и P 2.
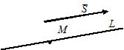
2) x − x 0 m = y − y 0 n = z − z 0 p − каноническое уравнение прямой L, которая проходит через точку M (x 0, y 0, z 0) параллельно вектору S ¯¯=(m, n, p). Вектор S ¯¯ является направляющим вектором прямой L.
3) x − x 1 x 2− x 1= y − y 1 y 2− y 1= z − z 1 z 2− z 1− уравнение прямой, которая проходит через две точки A (x 1, y 1, z 1) и B (x 2, y 2, z 2).
4) Приравнивая каждую из частей канонического уравнения 2 к прараметру t, получаем параметрическое уравнение прямой:
⎧⎩⎨⎪⎪ x = x 0+ mty = y 0+ ntz = z 0+ pt
6. Во-первых, две прямые на плоскости могут совпадать.
Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.
Во-вторых, две прямые на плоскости могут пересекаться.
В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. Пересечение прямых обозначают символом «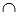 », к примеру, запись
», к примеру, запись 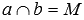 означает, что прямые а и b пересекаются в точке М. Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми. Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a перпендикулярна прямой b, то можно использовать краткую запись
означает, что прямые а и b пересекаются в точке М. Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми. Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a перпендикулярна прямой b, то можно использовать краткую запись 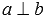 .
.
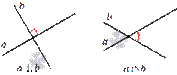
В-третьих, две прямые на плоскости могут быть параллельными.
Две прямые на плоскости называются параллельными, если они не имеют общих точек. Если прямая a параллельна прямой b, то используют символическое обозначение 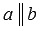 . Для более полной информации смотрите статью параллельные прямые, параллельность прямых.
. Для более полной информации смотрите статью параллельные прямые, параллельность прямых.
Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой. В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.

Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой. О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости.
Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.
|
|
|
Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:
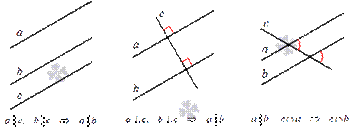
- если две прямые параллельны третьей прямой, то они параллельны между собой;
- если две прямые перпендикулярны третьей прямой, то они параллельны между собой;
- если на плоскости некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую.
7. Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
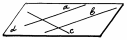
| a || b (прямая а параллельна прямой b) прямая с и прямая а не параллельны прямая с и прямая b не параллельны |
| рис. 8 |
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.
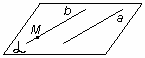
| M 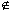 a b||а и М a b||а и М 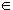 b (b - единственная) b (b - единственная)
|
| рис. 9 |
Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.
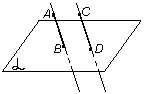
| отрезок СD || отрезку АВ |
| рис. 10 |
 2015-01-21
2015-01-21 2830
2830
