ЛОДУ n-го порядка с постоянными коэффициентами

Частным случаем линейных однородных дифференциальных уравнений являются ЛОДУ n-го порядка (n>2) с постоянными коэффициентами: y⁽ⁿ⁾ + p₁y^{(n – 1)} + p₂y^{(n – 2)} + … + p_ny = 0, где p_i,

i = 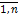, - числа.

Частные решения этого уравнения ищем в виде y = e^kx, где k – постоянное число.

Характеристическим для уравнения y⁽ⁿ⁾ + p₁y^{(n – 1)} + p₂y^{(n – 2)} + … + p_ny = 0 является алгебраическое уравнение n-го порядка вида

kⁿ + p₁k^{n – 1} p₂k^{n – 2} + … + p_{n – 1} k + p_n = 0.

Это уравнение имеет, как известно, n корней (в их числе могут быть и комплексные). Обозначим их через k₁, k₂, …, k_n.

Замечание: не все из корней уравнения kⁿ + p₁k^{n – 1} p₂k^{n – 2} + … + p_{n – 1} k + p_n = 0 обязаны быть различными. Так, в частности, уравнение (k – 3)² = 0 имеет два равных корня: k₁ = k₂ = 3. В этом случае говорят, что корень один (k = 3) и имеет кратность m_k = 2. Если кратность корня равна единице: m_k = 1, его называют простым.

Случай 1: все корни уравнения kⁿ + p₁k^{n – 1} p₂k^{n – 2} + … + p_{n – 1} k + p_n = 0 действительны и просты (различны). Тогда функции y₁ = e^k1x, y₂ = e^k2x, …, y_n = e^knx, являются частными решениями уравнения y⁽ⁿ⁾ + p₁y^{(n – 1)} + p₂y^{(n – 2)} + … + p_ny = 0 и образуют фундаментальную систему решений (линейно независимы). Поэтому общее решение уравнения y⁽ⁿ⁾ + p₁y^{(n – 1)} + p₂y^{(n – 2)} + … + p_ny = 0 записывается в виде

y = c₁e^k1x + c₂e^k2x + … + c_ne^knx.