Докажем существование такой пары многочленов.
Пусть f(x) = anxn+an-1 xn-1+...+ а1x+ а0
g(x) = bsхs+bs-1 хs-1+…+b1x+b0
При этом возможны два случая:
1-й случай: f(x) = 0 или cm f(x) < cm g(x), тогда
f(x) = g(x) • 0 + f(x)и искомые многочлены будут равны:
h(x) = 0, r(x) = f(x)
2-й случай: cm f(x) ³ cm g(x), и пусть cm f(x) = n, т.е. аn ¹ 0,
cm g(x)=s, т.е. bs ¹ 0
Тогда, вычтем из многочлена f(x) многочлен 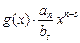 Получим:
Получим: 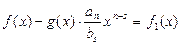 (1)
(1)
cm f1(x) < cm f(x), т.к. в процессе вычитания член anxn будет уничтожен.
Если cm f1(x) > cm g(x), то опять повторим процедуру понижения степени
(2) 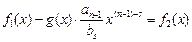 , где cm f2(x) < cm f1(x)
, где cm f2(x) < cm f1(x)
Если cm f2(x) ³ cm g (x), то опять повторим процедуру понижения степени до тех пор пока не получим многочлен fk(x), степень которого будет меньше ст. g(x), т.е. равенство: 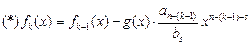
Складывая почленно равенства (1),(2)....,(k), получим:
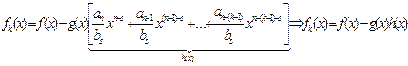 Обозначим fk(x)= r(x), т.к. его степень меньше cm g(x), тогда f(x)=g(x)h(x) + r(x) (**)
Обозначим fk(x)= r(x), т.к. его степень меньше cm g(x), тогда f(x)=g(x)h(x) + r(x) (**)
Докажем единственность такого представления:
Предположим противное, пусть
f(x)=g(x) h(x)+r(x),
где
cm r(х) < cm g(x) Ú r(x) = 0
и
f(x) = g(x)h1(x)+r1(x),
где
cm r1(х) < cm g(x) Ú r1(x)=0
Тогда, g(x) [h(x) – h1(x)]= r1(x) - r (x), cm g(x) + cm [h(x) – h1(x)] = =cm (r1(x) - r(х)), т.е. cm g(x) £ cm (r1(x) - r(x)), что противоречит определению отношения делимости многочленов с остатком. Следовательно, (h1(x) = h2(х)) & (r1(x) = r(x)). Таким образом, отношение делимости в кольце Р[х] обладает почти теми же свойствами, что и в кольце Z,однако есть и небольшие различия, например, кольцо Р[х] более богато обратимыми элементами, чем кольцо Z.
|
|
|
Так, относительно операции умножения в кольце Z всего два обратимых элемента 1, -1, а в кольце Р[х] это все многочлены нулевой степени, т.е. элементы поля Р.
Понятия HОД(f, g) и HOK(f, g) определяются с точностью до постоянного множителя (с), а в кольце Z с точностью до знака.
Действительно, если даны два многочлена f(x) и g(x), а d1(x) и d2(x) их НОД, то (d1(x) /d2(x)) & (d2(x) /d1(x)) => d1(x) = cd2(x) (см. св - во 3), т.е. НОК и НОД определяются с точностью до множителя из поля Р. Так же как и в кольце Z на основе доказанной выше теоремы можно записать алгоритм Евклида: для "f(x), g(x)ÎP[x], g(x) ¹ 0 и доказать, что последний остаток rn(х) ¹ 0 в этом алгоритме будет НОД(f(x), g(x)), что одновременно доказывает и существование НОД(f, g) для " f, g Î P[x].
Задача 1. В кольце Z5[х] найти НОД(f, g) и HOK[f, g], если
f(x) = x2 + 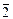 x +
x + 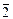 , g(x) =
, g(x) = 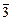 x3 –
x3 – 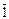
Решение. Для нахождения НОД(f, g)используем алгоритм Евклида. Делим "углом"' g(x) на f(х)
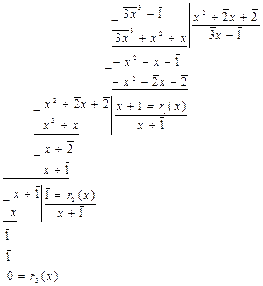
Итак HOД(f, g) = 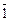
Для нахождения HOK[f, g] воспользуемся формулой
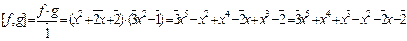 итак, HOK[f, g] =
итак, HOK[f, g] = 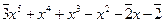
Замечание. В процессе выполнения алгоритма Евклида не только сами многочлены f(x) и g(x), но и получаемые остатки можно умножать на любые числа (не равные нулю), чтобы в частном получались только целые коэффициенты. При этом, конечно, частное искажается, остаток от деления остается с точностью до ассоциированности.
|
|
|
Однако, этого делать нельзя, когда решаем
Задачу 2. В кольце Q[x] с помощью алгоритма Евклида найти линейное представление НОД(f, g), если
f(x) = x5 - 5x4 - 2х3 + 12х - 2х + 12
g(x)= х3 – 5x2 – 3x + 17
Решение.
Найти линейное представление - это значит найти многочлены u(х) и v(x): d(x) = f(x)u(x) + g(x)v(x). Делим f(х) на g(x):
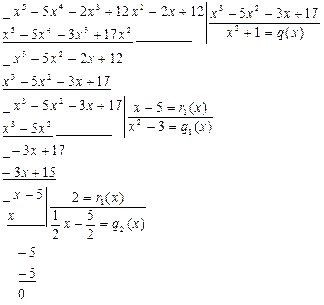
0=r3(x)
Итак, HOД(f, g)=2
Теперь запишем процесс деления многочленов в виде равенств:
f(x) = g(x)•(x2 + l) + (x - 5), g(x) = (x - 5)•(x2 - 3) + 2
Выразим из последнего равенства (f,g) = 2 2 = g(x) - (x - 5)•(x2 - 3) (*)
Из первого равенства выразим остаток r(х) = (х - 5), х - 5 = f(x) - g(x)(x2- 1) и подставим в равенство (*).
Получим:
2 = g(x) - [f (x) - g(x)(x2 + 1)](х2 - 3)
2 = g(x) - f(х)(х2 + 3) + g(x)(x2 + 1)(х2 - 3)
2 = g(x)[l + (х2 + 1)(х2 - 3)] + f (х)(3 - х2)
v(x) = l + (x2+l)(x2 -3) = 1+х4 - 3х2 + х2 - 3=х4 - 2х2 - 2
Ответ: u(x)=3 - x2, v(x)=x4 – 2x2 -2
Замечание. В этой задаче использовались неполные частные, поэтому нельзя домножать многочлены на множители из поля Q.
Определение 2. Многочлены f(x) и g(x) называются взаимно простыми, если (f, g)=c, где с Î Р.
Чтобы снять неоднозначность, вводится понятие нормированного многочлена.
Определение 3. Многочлен f(x) Î P[x] называется нормированным, если коэффициент при его старшем члене равен 1.
Например, f(x)=x5 + 3x4 - 2x2 + 2. Тогда, если f(x) и g(x) нормированные и взаимно простые, то (f, g)=l.
Имеет место следующая теорема:
Критерий взаимной простоты: (f, g) = l Û $ u, v Î P[x]:
f(x)u(x) + g(x)v(x) = 1.
 2015-02-27
2015-02-27 636
636