Логические функции

Отличительной особенностью логических функций состоит в том, что они принимают значения в конечных множествах. Иначе говоря, область значений логической функции всегда представляет собой конечную совокупность чисел, символов, понятий, свойств и, вообще, любых объектов.

Если область значений функций содержит k различных элементов, то она называется k-значной функцией.

Переименуем элементы области значений функции числами 1, …,k (или обозначают буквами). Перечет всех символов, соответствующих области значений, называют алфавитом, а сами символы - буквами этого алфавита (латинского, русского или другого алфавита, порядковые числа или любые другие символы).

Логические функции могут зависеть от одной, двух и любого числа переменных (аргументов) х₁, …, х_n.

В теоретико-множественном смысле логические функции n переменных y=f(x₁, …, x_n) представляет собой отображение множества наборов (n-мерных векторов, кортежей последовательностей) вида (х₁, х₂, …, х_n) являющегося областью ее определения, на множество ее значений.

Если аргументы принимают значения из того же множества, что и сама функция, то ее называют однородной функцией.

Логическую функцию можно также рассматривать как операцию, заданную законом композиции

Х₁ 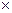Х₂ 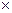… 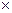Х_n> N, где Х₁, …, Х_n – множества, на которых определены аргументы

х₁ 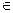Х₁, х₂ 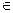Х₂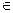, …, х_n Х_n.

Если Х₁= Х₂=…= Х_n= N, и однородная функция, рассматриваемая как закон композиции

N ⁿ> N, определяет n-местную операцию на конечном множестве N.

Областью определения однородной функции y=f(x₁, x₂, …, x_n) служит множество наборов (х₁, …, х_n), называемых словами, где каждый из аргументов х₁, х₂, …, х_n заменяется буквами k-ичного алфавита (0,1,..., (k-1)). Количество n букв в данном слове определяет его длину.

Очевидно, число всевозможных слов длины n в k-ичном алфавите равно kⁿ. Так как каждому такому слову имеется возможность представить одно из k значений множества N, то общее количество однородных функций от n переменных выражается числом .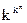

Если буквами алфавита служат числа от 0 до (k-1), то каждое слово (х₁, х₂, …, х_n) символически представляется упорядоченной последовательностью n таких чисел и рассматривается как запись n-разрядного числа в позиционной системе счисления с основанием k, то есть

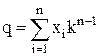
или х₁k^n-1+ х₂k^n-2+…+ х_n-1k¹+ х_nk⁰=q.

Числа q=0,1,…,kⁿ-1 служат номерами слов и тем самым на множестве всех слов вводится естественная упорядоченность. Аналогично номерами функций можно считать kⁿ разрядные числа в той же системе счисления.

Различны слова длины n в данном алфавите образуется как n-перестановки с повторениями.

Так в трехзначном алфавите (0,1,2) словами длины 4 будут всех четырехразрядные числа с основанием k=3, т.е. 0000, 0001,0002,0010, 0011, …, 2221, 2222 которые соответствуют десятичным числам от 0 до 80=2•3³+2•3²+2•3¹+2•3⁰.

Поставить каждому такому числу в соответствии одну из букв алфавита {0,1,2}, получим некоторую функцию четырех переменных

f(x₁, x₂, x₃, x₄),

причем количество таких функций выразится числом .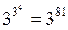

Наиболее простым и важнейшим классом однородных функций являются двузначные (булевы) функции (иногда ее называют переключательной). Функция f(x₁, x₂, …, x_n-1, x_n) принимает два значения 0,1 и зависит от переменных x_i 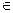{0,1}, i= .

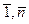Областью определения булевой функции служит совокупность всевозможных n-мерных наборов из 0 и 1, а для ее задания достаточно указать, какие значения функции соответствуют каждому из этих наборов, т.е. осуществить табличные значения функции.

x1, x2, …, xn-1, xn	f (x1, x2, …, xn-1, xn)
0 0 … 0 0	f ( 0, 0, …, 0, 0 )
0 0 … 0 1	f ( 0, 0, …, 0, 1 )
… … … … …	… … …… … … …
1 1 … 1 0	f ( 1, 1, …, 1, 0 )
1 1 … 1 1	f ( 1, 1, …, 1, 1 )

Каждому набору α=(α₁, …,α_n) α_i 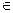{0,1} становится в соответствии число

N=α₁2^n-1+…+ α_n-12+ α_n.

Наборам (0, 0, …, 0, 0), (0, 0, …, 0, 1), …, (1, 1, …, 1, 1) соответствуют числа 0,1, …, 2^n-1.

Легко видеть, что число n-мерных наборов из 0 и 1 равно 2ⁿ.

Если зафиксировать n переменных x₁, x₂, …, x_n, то разные функции от переменных x₁, x₂, …, x_n задаются разными таблицами. Число различных таблиц равно числу всех функций от переменных x₁, x₂, …, x_n. Число булевых функций от n переменных x₁, x₂, …, x_n равно .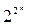

Познакомимся с другими способами задания булевой функции.

Сначала познакомимся с функцией одной и двух переменных, которые иногда называют «элементарными» функциями».

ФУНКЦИИ АЛГЕБРЫ ЛОГИКИ И ИХ ОСНОВНЫЕ СВОЙСТВА.

Рассмотрим множество векторов 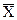={ x₁, x₂, …, x_n }, пусть координаты этих векторов принимают значения 0 или 1. Таким образом, множество Х состоит из 2ⁿ различных векторов.

Совокупность координат некоторого фиксированного вектора 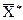из множества 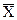будем называть двоичным набором или просто набором.

Сопоставим каждому вектору Х число 0 или 1, т.е. произведем однозначное отображение Х на множество Y={0,1}.