Для решения вопроса о сложении сил, приложенных в различных точках твердого тела и направленных как угодно в пространстве в начале выясним, при каких условиях силу, приложенную у твердому телу в данной точке, можно переносить в любую точку (центру).
Допустим, что сила 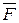 действует на тело в точке А, как показано на рис.4.1. Теперь попробуем эту силу параллельно самой себе перенести в точку В, называемую центром приведения. Для этого докажет следующую лемму: Всякую силу, приложенную к твердому телу из ее точки приложения можно переносить в любую другую точку, добавляя при этом одну пару сил, момент которой равен произведению силы на кратчайшее расстояние от центра приведения до линии ее действия.
действует на тело в точке А, как показано на рис.4.1. Теперь попробуем эту силу параллельно самой себе перенести в точку В, называемую центром приведения. Для этого докажет следующую лемму: Всякую силу, приложенную к твердому телу из ее точки приложения можно переносить в любую другую точку, добавляя при этом одну пару сил, момент которой равен произведению силы на кратчайшее расстояние от центра приведения до линии ее действия.
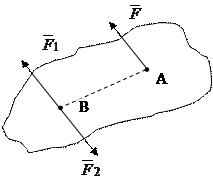 |
Рис.4.1.
Докажем эту лемму:
Согласно аксиоме 2, действие силы 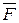 не изменится, если в любой другой точке тела приложить две равные и противоположно направленные силы
не изменится, если в любой другой точке тела приложить две равные и противоположно направленные силы 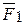 и
и 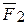 , т.е.
, т.е. 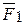 =-
=- 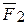 . Причем их можно выбирать так, чтобы по модулю они были равны заданной силе F1=F2=F. Тогда сила
. Причем их можно выбирать так, чтобы по модулю они были равны заданной силе F1=F2=F. Тогда сила 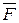 ~(
~(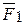 ,
, 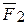 ,
, 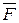 ), так как (
), так как (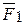 ,
, 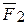 )~0. Но, с другой стороны три силы
)~0. Но, с другой стороны три силы 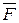 ,
, 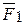 ,
, 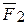 можно рассматривать как совокупность силы
можно рассматривать как совокупность силы 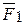 и пары (
и пары (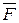 ,
, 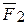 ). Таким образом, получается, что сила
). Таким образом, получается, что сила 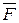 , приложенная в точке А, эквивалентна такой же силе
, приложенная в точке А, эквивалентна такой же силе 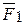 , но приложенной в произвольно выбранной точке В и паре сил (
, но приложенной в произвольно выбранной точке В и паре сил (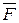 ,
, 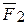 ), момент которой равен моменту силы
), момент которой равен моменту силы 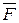 относительно точки В. Здесь пара (
относительно точки В. Здесь пара (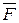 ,
, 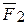 ) называется присоединенной, а точка В - центром приведения. Доказанную лемму обычно называют леммой о параллельном переносе силы. Этот метод был предложен французским ученым Пуансо (1777-1859) и назывался приведением силы к заданному центру.
) называется присоединенной, а точка В - центром приведения. Доказанную лемму обычно называют леммой о параллельном переносе силы. Этот метод был предложен французским ученым Пуансо (1777-1859) и назывался приведением силы к заданному центру.
|
|
|
Пользуясь этой леммой докажем следующую основную теорему статики твердого тела.
Теорема Пуансо. Всякую систему сил, как угодно расположенных в пространстве, всегда можно привести к одной силе, приложенной в центре приведения и равной векторной сумме всех заданных сил, и паре, момент которой равен сумме моментов этих сил относительно точки приведения.
Переходим к доказательству этой теоремы. Пусть дана система сил 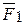 ,
, 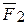 ,
, 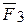 ,…,
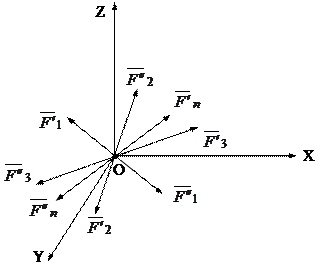
,…, 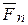 приложенных в точках А1, А2, А3,…, Аn, какого-либо твердого тела и направленных как угодно в пространстве (рис.4.2). При этом радиус векторов точки приложения силы
приложенных в точках А1, А2, А3,…, Аn, какого-либо твердого тела и направленных как угодно в пространстве (рис.4.2). При этом радиус векторов точки приложения силы 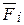 от этого центра обозначим через
от этого центра обозначим через 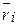
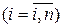 .
.
 | |||
 | |||
Рис.4.2.
Возьмем произвольную точку за центр О и приведем все силы к этой точке (пользуясь леммой). В результате получим систему сходящихся сил 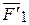 ,
, 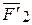 ,
, 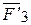 ,…
,… 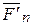 приложенных в точке О и присоединенные пары (
приложенных в точке О и присоединенные пары (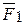 ,
, 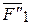 ), (
), (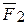 ,
, 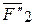 ), (
), (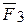 ,
, 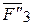 ), …, (
), …, (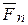 ,
, 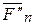 ) полученные при последовательном переносе системы заданных сил в точку О соответственно с моментами
) полученные при последовательном переносе системы заданных сил в точку О соответственно с моментами 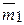 ,
, 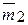 ,
, 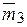 ,…,
,…, 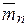 .
.
Складывая силы 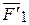 ,
, 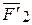 ,
, 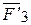 ,…
,… 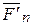 , приложенные в точке О, находим
, приложенные в точке О, находим
|
|
|
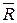 =
= 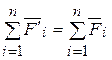 (4.1)
(4.1)
Такая сумма всех сил называется главным вектором.
Затем, складывая присоединенные пары (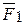 ,
, 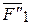 ), (
), (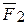 ,
, 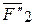 ), (
), (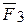 ,
, 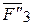 ), …, (
), …, (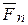 ,
, 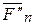 ), находим равнодействующую пар, момент которой равен сумме моментов составляющих пар, т.е.
), находим равнодействующую пар, момент которой равен сумме моментов составляющих пар, т.е.
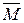 =
= 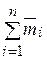 (4.2)
(4.2)
Если учесть, что каждая присоединенная пара характеризуется моментом своей составляющей относительно точки приведения, т.е. через 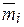 =
= 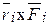 , то выражение (4.2) дает следующую векторную сумму моментов всех заданных сил относительно точки приведения
, то выражение (4.2) дает следующую векторную сумму моментов всех заданных сил относительно точки приведения
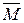 =
= 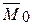 =
= 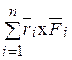 . (4.3)
. (4.3)
Такую сумму называют главным моментом системы относительно этого центра.
Итак, силы, расположенные как угодно в пространстве, всегда могут быть приведены к одной силе, равной их главному вектору 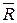 , приложенной в произвольной точке О и к паре (
, приложенной в произвольной точке О и к паре (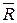 ,
, 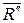 ), момент которой равен главному моменту данных сил относительно точки
), момент которой равен главному моменту данных сил относительно точки 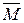 =
= 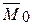 .
.
Следует отметить, что выбор центра приведения не отражается на численном значении и направлении главного вектора 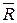 , но влияет на модуль и направление главного момента
, но влияет на модуль и направление главного момента 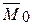 .
.
Для вычисления главного вектора 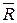 и главного момента
и главного момента 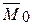 системы сил, произвольно расположенных в пространстве, воспользуемся методом проекции. Для этого обозначив проекции главного вектора на оси координат через Rx, Ry, Rz, согласно (4.1), имеем
системы сил, произвольно расположенных в пространстве, воспользуемся методом проекции. Для этого обозначив проекции главного вектора на оси координат через Rx, Ry, Rz, согласно (4.1), имеем
Rx= 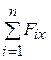 ; Ry=
; Ry= 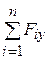 ; Rz=
; Rz= 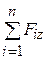 , (4.4)
, (4.4)
где Fix, Fiy, Fiz-проекции сил 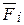 (i =
(i = 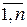 ) соответственно на оси координат X,Y и Z. Модуль главного вектора
) соответственно на оси координат X,Y и Z. Модуль главного вектора 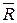 определяется из
определяется из
К= 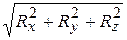 . (4.5)
. (4.5)
Здесь Rx, Ry, Rz вычисляются по формуле (4.4).
Так как 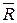 является векторной величиной, то кроме численного значения необходимо знать его направление. Оно находится при помощи направляющих косинусов, известных из курса векторной алгебры
является векторной величиной, то кроме численного значения необходимо знать его направление. Оно находится при помощи направляющих косинусов, известных из курса векторной алгебры
cos(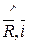 )=
)= 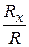 ; cos(
; cos(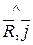 )=
)= 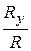 ; cos(
; cos(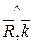 )=
)= 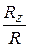 . (4.6)
. (4.6)
Откуда
(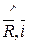 )=arccos
)=arccos 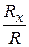 ; (
; (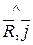 )=arccos
)=arccos 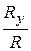 ; (
; (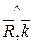 )=arccos
)=arccos 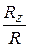 . (4.7)
. (4.7)
Формулы (4.6) и (4.7) дают возможность определить соответственно направляющие косинусы и углы между главными вектором и прямоугольными осями координат.
Если проекции главного момента 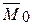 на декартовой оси X,Y,Z обозначим через M0x, M0y, M0z, то
на декартовой оси X,Y,Z обозначим через M0x, M0y, M0z, то
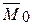 = M0x×
= M0x× 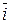 + M0y×
+ M0y× 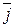 + M0z×
+ M0z× 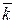 (4.8)
(4.8)
С другой стороны, согласно формулы (4.3), имеем
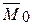 =
= 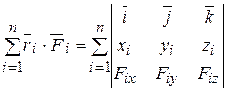 =
=
= 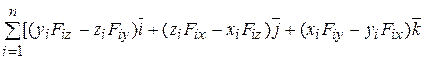 , (4.9)
, (4.9)
где через x i, yi, z i обозначены проекции радиуса-вектора 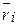 на соответствующие оси координат. Далее сравнивая (4.8) с (4.9), находим
на соответствующие оси координат. Далее сравнивая (4.8) с (4.9), находим
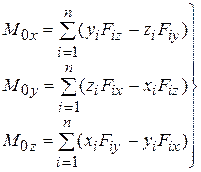 (4.10)
(4.10)
Следовательно, модуль и направление вектора 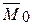 определяются формулами:
определяются формулами:
М0= 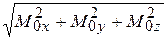 (4.11)
(4.11)
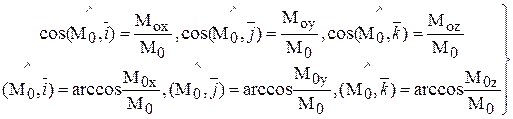 (4.12)
(4.12)
Заметим, что так как силы системы расположены в пространстве совершенно произвольно, то главный момент 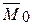 может быть направлен под какие угодно углом. Для определения этого угла воспользуемся формулой, выражающей скалярное произведение векторов
может быть направлен под какие угодно углом. Для определения этого угла воспользуемся формулой, выражающей скалярное произведение векторов 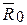 и
и 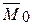
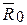 ×
× 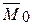 =R0M0cos(
=R0M0cos(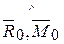 )
)
Откуда
cos(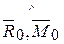 )=
)= 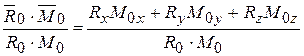 (4.13)
(4.13)
или в соответствии с формулами (4.6) и (4.12), имеем
cos(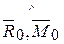 )=cos(
)=cos(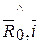 )cos(
)cos(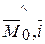 ) + cos(
) + cos(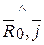 )cos(
)cos(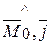 ) +
) +
+ cos(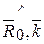 )cos(
)cos(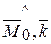 ) (4.14)
) (4.14)
Если к твердому телу приложена плоская система сил, то из трех прямоугольных декартовых осей координат X,Y,Z достаточно выбрать две, например, х, у. Тогда модуль и направление главного вектора 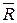 определяются по формулам
определяются по формулам
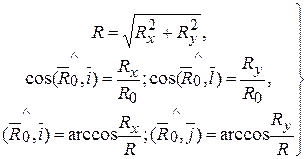 (4.15)
(4.15)
где
Rx= 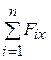 ; Ry=
; Ry= 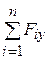 .
.
Для этого случая все присоединенные пары сил лежат в одной плоскости. Следовательно, момент эквивалентной им пары сил, равный главному моменту системы сил относительно центра приведения определяется как алгебраическая сумма моментов сил относительно этого центра
M=M0= 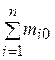 (4.16)
(4.16)
Теперь рассмотрим возможные частные случаи при приведении системы сил, действующих на тело к выбранному центру. Всего таких случаев может быть пять:
1. 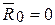 ,
, 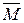 =
= 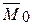 =0. В этом случае заданная система сил уравновешена.
=0. В этом случае заданная система сил уравновешена.
2. 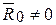 ,
, 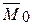 =0. Заданная система сил эквивалентна одной силе
=0. Заданная система сил эквивалентна одной силе 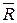 , т.е. приводится к равнодействующей, линия действия которой проходит через центр приведения.
, т.е. приводится к равнодействующей, линия действия которой проходит через центр приведения.
3. 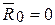 ,
, 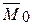 ¹0. Система сил приводится к одной паре.
¹0. Система сил приводится к одной паре.
4. 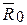 ¹0,
¹0, 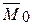 ¹0 и cos(
¹0 и cos(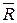 ,
, 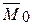 )=0. Заданная система сил приводится к одной силе.
)=0. Заданная система сил приводится к одной силе.
5. 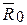 ¹0,
¹0, 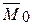 ¹0 и cos(
¹0 и cos(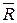 ,
, 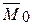 )¹0. В этом случае заданная система сил приводится к динамическому винту.
)¹0. В этом случае заданная система сил приводится к динамическому винту.
 2015-02-27
2015-02-27 3538
3538
