Решение задачи коммивояжера с учетом реальной сети дорог на основе интеграции жадного алгоритма и алгоритма нахождения кратчайших путей

М.А. Беляева, Д.А. Крючкова

ОАО «ВолгаТелеком» - крупнейший оператор связи России. В состав компании входит одиннадцать филиалов, работающих в семи областях и четырех республиках Приволжского Федерального округа. На территории Оренбургской области ОАО «ВолгаТелеком» представлен Оренбургским филиалом, в состав которого входит Районный телекоммуникационный узел (РТУ) п. Саракташа.

В настоящее время телефонная связь отвечает всем современным требованиям, одним из которых является улучшение ее качественных характеристик, то есть повышение слышимости, снижение помех, др.

Несмотря на отлаженную работу телефонной связи, возникают сбои в работе абонентов и на предприятие поступают звонки от абонентов о возникших неполадках. Поэтому возникает задача определения оптимальных путей проезда электромонтеров к местам аварий и обратно.

Задача коммивояжера (в дальнейшем сокращённо - ЗК) является одной из знаменитых задач комбинаторики. Она была поставлена в 1934 году. В своей области (оптимизации дискретных задач) ЗК служит своеобразным полигоном, на котором испытываются всё новые методы. Она является также тестом для проверки и сравнения различных алгоритмов решения комбинаторных задач оптимизации.

Существует классическая постановка задачи коммивояжера, которая в простейшей постановке формулируется следующим образом.

Пусть имеется множество М населенных пунктов. Необходимо составить такой маршрут посещения этих пунктов, который проходит через каждый пункт только один раз и длина которого минимальна.

В графовой постановке задача коммивояжера определяется следующим образом.

Дан полный орграф G, дугам которого приписаны произвольные веса С = [с_ij], i,j=1,...,n. Требуется найти такой гамильтонов цикл (цепь), который имеет наименьший общий вес. Задача нахождения гамиль­тонова цикла с наименьшим весом хорошо известна в литературе как задача коммивояжера. Если орграф G не полный, то его можно рассматривать как полный орграф, приписывая отсутствующим дугам бесконечный вес.

При такой постановке задачи можно использовать множество методов решения, как точных, таки приближенных. Все точные методы - это методы перебора возможных решений, а приближенные - это: метод ветвей и границ, алгоритм ближайшего непосещенного города, генетический алгоритм, деревянный алгоритм и др.

Однако такая постановка идеальная, она не учитывает реальный условий задачи Данная постановка предполагает два взаимосвязанных, но практически невыполнимых предположения:

- коммивояжер (или транспортное средство) всегда может передвигаться в данном регионе по прямой линии;

- вся поверхность региона - это идеально гладкая и твердая плоскость, пригодная для движения транспортных средств.

Рассмотрим постановку задачи, учитывающую реальные возможности движения коммивояжера по региону с привязкой к дорожной сети. В реальной жизни приходится добираться до мест неполадок объездом, используя повторные посещения некоторых пунктов и перекрестков из-за недостаточно разветвленной сети дорог, отсутствия прямых дорог между пунктами.

Постановка задачи коммивояжера с учетом реальной сети дорог.

В регионе с развитой сетью дорог имеется:

- множество М населенных пунктов;

- множество N перекрестков (развилок) вне населенных пунктов;

- множество К участков дорог.

Участком дороги назовем дорогу от пункта А до пункта Б, причем пункт - это населенный пункт или перекресток.

Необходимо составить такой маршрут посещения населенных пунктов, чтобы длина маршрута, включая суммарные повторные пробеги по участкам дорог, была минимальной.

В данной постановке учитывается то обстоятельство, что из-за конечных возможностей дорожной сети все-таки возможны повторные посещения населенных пунктов и возвраты к перекресткам (развилкам) дорог. Однако не существует метода, который сразу мог бы привести к оптимальному маршруту при такой постановке. Если время ожидания результата позволяет, то необходимо реализовать алгоритм полного перебора вариантов, но если время не позволяет, можно решить задачу предложенным нами приближенным алгоритмом.

Авторами разработан приближенный алгоритм решения сформулированной задачи на основе синтеза жадного алгоритма решения задачи коммивояжера[1] и алгоритма нахождения кратчайших путей Флойда [2].

Пусть дан граф G=(X,A), Х={x₁,x₂,…,х_n},С= [c_ij)], i = j = 1, …, n,

где G-исходный граф;

Х-множество вершин графа (населенные пункты области);

А-множество дуг графа (отрезков дорог между населенными пунктами);

n – число вершин графа G;

С-матрица весов дуг графа G.

Предполгается, что в начальной матрице весов c_ij = 0 для всех i = 1, 2,..., n и c_ij = ¥, если в графе отсутствует дуга (x_i, x_j).

Укрупненный алгоритм нахождения оптимального квазигамильтонова цикла по населенным пунктам доставки ремонтной бригады

Шаг 1. Нахождение матрицы длин кратчайших путей D и таблицы кратчайших путей Т между всеми вершинами графа (расселенными пунктами области).

Шаг 1.1 Положить k = 0.

Итерация

Шаг 1.2 k = k + 1.

Шаг 1.3 Для всех i ¹ k, таких, что с_ik ¹ ¥, и для всех j ¹ k, таких, что с_kj ¹ ¥, введем операцию

c_ij = min [c_ij, (c_ik + c_kj)]

Шаг 1.4 а) Если c_ii< 0, то в графе G существует цикл отрица­тельного веса, содержащий вершину x_i, и решения нет. Останов.

б) Если все с_ij 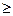0 и k = n, то получено решение. Матрица [c_ij] дает длины всех кратчайших путей. Останов.

в) Если все c_ii 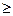0, но k < n, то вернуться к шагу 1.2.

Шаг 1.5 D=C.

Шаг 1.6 Нахождение таблицы кратчайших путей между всеми вершинами графа при помощи рекурсивной процедуры с использо­ванием соотношения:

l(х¢_i) + c (х¢_i, x_i) = l(x_i),

где х¢_i –вершина,непосредственно предшествующая вершине x_i в кратчайшем пути к x_i,

Шаг 2 Определение гамильтонова цикла по отмеченным вершинам графа G (требующими ремонта телефонной сети населенными пунктами области).

Шаг 2.1: пусть D = d_ij – матрица весов путей графа G, найденная на шаге 1, i=j=1, …, n, x_k – текущая вершина.

Шаг 2.2 x_k = x_l, отметить вершину как пройденную, т.е. внести ее в множество Q, хранящее последовательность таких вершин.

Шаг 2.3 Если " x_k ÎQ, k = 1, …, n, наикратчайший путь построен, то осуществляется возврат в точку отправления (добавить в множество Q исходную вершину), алгоритм завершен, иначе к шагу 2.4.

Шаг 2.4 Методом сравнений найти вершину x_l, такую что:

d_kl=min(d_kj), j = 1, …, n && j¹k,

т.е. x_l – ближайшая вершина от текущей вершине x_k.

Шаг 2.5 Если вершина x_l ÎQ, то возвратиться к шагу 2.4, причем j¹l, иначе к шагу 2.2.

Шаг 3 Восстановление полного квазигамильтонового цикла с учетом кратчайших путей по промежуточным вершинам графа, найденным на шаге 1.

В алгоритме используются переменные:

G – исходный граф;

n – число вершин графа G;

D – матрица весов исходного графа G;

d_ij – вес ребра между i -той и j -той вершинами, i = j = 1, …, n;

x_k – текущая вершина, k = 1, …, n;

x_l – ближайшая вершина от текущей, l = 1, …, n -1;

d_kl – вес ребра между текущей и ближайшей вершинами;

Q – множество, хранящее последовательность пройденных вершин в порядке их посещения.

Рассмотрим реализацию разработанного алгоритма на примере. Для РТУ (п. Саракташ) необходимо решить следующую задачу.

При заданных населенных пунктах п. Саракташ, расстояниях между ними и карте дорог требуется определить оптимальный маршрут доставки бригад по ремонту телефонной связи. Допустим, что в бюро ремонтов поступило четыре вызова о неполадках из таких населенных пунктов как Карагузино, Гавриловка, Кабанкино и Черный Отрог. Начальнику кросса требуется направить ремонтную бригаду таким образом, чтобы маршрут был наикратчайшим с учетом реальной сети дорог.

Матрица расстояний между населенными пунктами представлена в таблице 1.

Таблица 1 – Матрица расстояний между населенными пунктами

Населенные пункты	Карагузино	Гавриловка	Кабанкино	Черный Отрог	Саракташ
Карагузино		9,84	20,68	29,84	36,64
Гавриловка	9,84		11,86	21,02	27,82
Кабанкино	20,68	11,86		9,06	31,72
Черный Отрог	29,84	21,02	9,06
Саракташ	36,64	27,82	31,72

На рисунке 1 представлено решение задачи нахождения квазигамильтонова цикла.

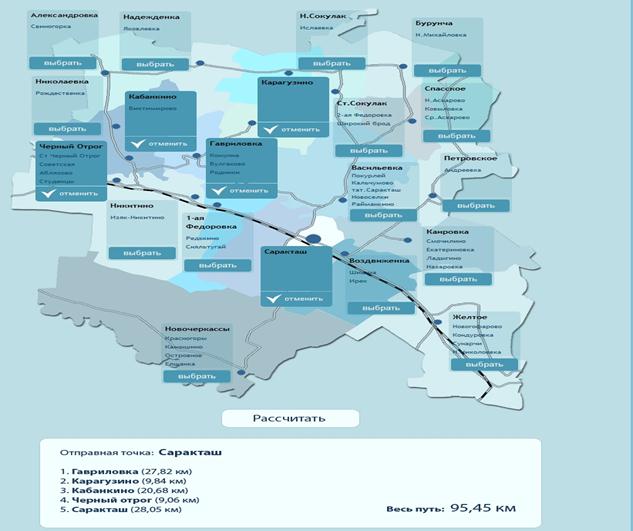
Рисунок 1- Решение задачи оптимальной доставки ремонтной бригады с учетом реальной сети дорог

Таким образом, нами разработан алгоритм решения задачи коммивояжера с учетом реальной сети дорог на основе нахождения квазигамильтонова цикла. Данный алгоритм использует интеграцию жадного алгоритма нахождения гамильтонова цикла и алгоритма нахождения кратчайших путей Флойда. Разработанный алгоритм реализован на примере определения оптимального пути доставки бригады по ремонту телефонной связи, что позволяет сократить транспортные расходы на доставку ремонтной бригады.

Список литературы

1. Алексеев, В. Е. Графы и алгоритмы. Структуры данных. Модели вычислений: учебник / В. Е. Алексеев, В. А. Таланов. - М.: Интернет-Ун-т Информ. Технологий: Бином. Лаборатория знаний, 2006. - 320 с

2. Харари Ф. Теория графов. Пер. с англ./ Ф. Харари - Едиториал УРСС, 2006.- 501 с.