2015-02-27
713
В логике первого порядка (логике предикатов) условия эффективного применения метода резолюций для доказательства теорем такие же, как и в логике высказываний. Напоминаем, что одно из этих условий – это представление теорем в ПКНФ. Правила эквивалентных преобразований формул, введенные в логике высказываний, равнозначны и для логики первого порядка. Однако присутствие в формулах кванторов всеобщности и существования затрудняет применение теорем к ПКНФ.
В связи с этим дополнительно вводятся ряд правил, позволяющих исключить указанные кванторы из формул. Эти правила делятся на две группы:
1) Правила образования предваренных нормальных форм (ПНФ);
2) Правила образования Скулемовских стандартных форм (ССФ).
Рассмотрим эти формы и правили их образования.
Формула F находится в предваренной нормальной форме (ПНФ), тогда и только тогда, когда она имеет вид:
где каждое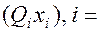 
1,n есть или 
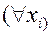), ил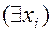и 
, и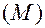 
есть формула, не содержащая кванторов. 
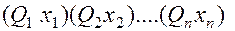называется префиксом, а 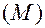- матрицей формулы F.
Например, в формуле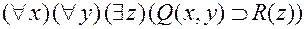 
префикс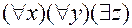 
предваряет матрицу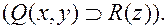 
Рассмотрим правила эквивалентных преобразований формул, содержащих кванторы.
Пусть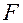 
есть формула, содержащая свободную переменную 
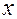. Будем обозначать эту формулу 
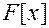. Пусть 
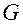есть формула, которая не содержит переменной 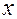. Пусть 
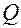есть квантор 
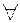или квантор 
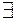. Тогда правила следующие:
1a)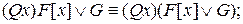 
1b)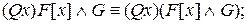 
2a) 
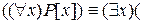
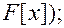
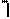
2b)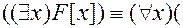 
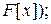
3a)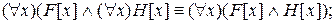 
3b)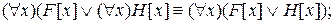 
4a) (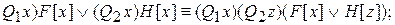
4b)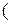 
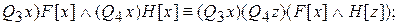
Используя правила эквивалентных преобразований формул логики высказываний и указанные восемь правил, всегда можно преобразовать любую формулу в ПНФ. Рассмотрим пример.
Приведем формулу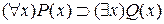 
к ПНФ. Используя правило исключения связки импликации, получим:
.
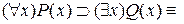
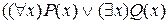По правилу 2a имеем:
.
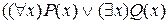
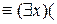
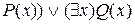Наконец, используя правило 3b, получим:
.
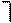
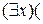
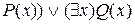
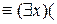
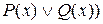Формула в правой части последнего соотношения представлена в ПНФ.
Скулемовская стандартная форма – это ПНФ, в префиксе которой отсутствуют кванторы существования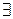 
, а матрица 
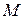является ПКНФ. Из этого определения становится очевидным, что скулемовские преобразования формул направлены на исключение кванторов существования из предваренных нормальных форм. Рассмотрим эти правила преобразования.
Пусть формула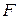 
находится в предваренной нормальной форме, где 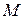есть ПКНФ. Положим, что 
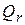есть квантор существования в префиксе 
.
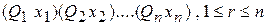Если никакой квантор всеобщности не стоит в префиксе левее 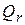, то выберем новую константу 
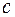, отличающуюся от других констант, входящих в 
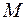, заменим все 
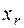, встречающиеся в 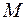, на константу 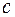и вычеркнем 
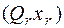из префикса. Если 
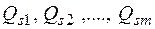- список всех кванторов всеобщности, встречающихся левее , 
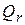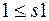
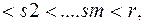то выберем новый 
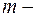местный функциональный символ 
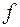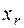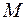, отличающийся от других функциональных символов, заменим все в на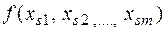 
и вычеркнем 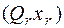из префикса. Затем этот процесс применяем для всех кванторов существования в префиксе; последняя из полученных формул есть ССФ – скулемовская стандартная форма. Константы и функции, используемые для замены переменных квантора существования, называют скулемовскими константами и функциями. Рассмотрим пример.
Получим ССФ для формулы:
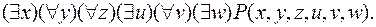
Здесь левее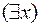 
нет никаких кванторов всеобщности, левее 
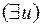стоят 
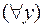и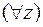 
, а левее 
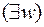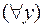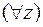стоят , и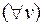 
. Следовательно, заменим переменную 
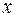на константу 
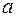, переменную 
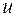на двухместную функцию 
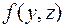, переменную 
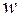на трехместную функцию 
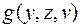. Таким образом, после указанных замен и изъятия кванторов существования получим следующую стандартную форму для написанной выше формулы:
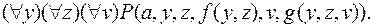
Рассмотренные правила эквивалентных преобразований дают возможность представить любую теорему логики предикатов в скулемовской стандартной форме. Так как префикс в этой форме содержит только кванторы всеобщности, то это означает, например, для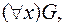 
что форма получает значение И, если 
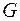истинно для каждого 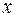из области 
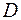(а в противном случае получает значение Л), то это дает право рассматривать 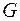как простое высказывание и квантор всеобщности, связывающий 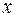, вычеркнуть из префикса. В равной мере этот вывод относится и к кванторам всеобщности, связывающим другие переменные. Поэтому для доказательства теорем в логике предикатов можно использовать только матрицы, находящиеся в ПКНФ.
В логике предикатов доказана также следующая теорема.
Пусть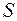 
- множество дизъюнктов, которые представляют ПКНФ в скулемовской стандартной форме некоторой формулы (теоремы) 
. Тогда формула противоречива в том и только в том случае, когда множество 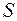противоречиво.
Механизм применения метода резолюций, который использовался для доказательства теорем в логике высказываний, может быть применен и в логике предикатов. Однако при этом возникают три существенных вопроса:
1) как найти контрарные пары для дизъюнктов, содержащих переменные?
2) как вычислить резольвенту из дизъюнктов, содержащих переменные?
3) Как извлечь максимальную пользу из обратной дедукции с целью повышения эффективности метода резолюций?
Ответы на эти вопросы вносят некоторую специфику в алгоритм метода резолюций. Вернуться
