Основные понятия. Равномерно сходящиеся ряды обладают рядом свойств, которые и делают такие ряды очень важными для приложений

Равномерно сходящиеся ряды обладают рядом свойств, которые и делают такие ряды очень важными для приложений. Дело в том, что при определенных условиях функциональные ряды можно дифференцировать почленно, интегрировать, менять местами знаки предела и суммы и т.п. Это дает возможность успешно использовать разложение в ряд функций при решении алгебраических, дифференциальных и интегральных уравнений.

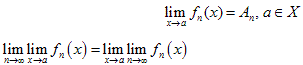Теорема 1. Пусть функциональная последовательность { fn (x)} равномерно сходится к f (x) на промежутке X и при каждом n существует конечный предел.

Тогда последовательность { An } сходится и

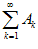Теорема 2. Если функциональный ряд сходится равномерно на промежутке X и

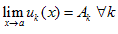
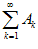существуют конечные пределы, где a Î X, то ряд сходится, и

верно равенство

.

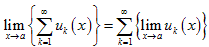Теорема 3. Пусть функциональная последовательность { fn (x)} непрерывна на промежутке X и равномерно сходится к f (x) на этом промежутке. Тогда f (x) непрерывна на промежутке X.

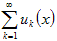Теорема 4. Если все функции uk (x) непрерывны на промежутке X и ряд сходится на этом промежутке, то сумма ряда S (x) является непрерывной

функцией на промежутке X.

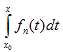Теорема 5. Если последовательность непрерывных функций fn (x) сходится

равномерно на сегменте [ a, b ] к функции f (x), то последовательность сходится

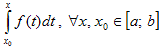равномерно на сегменте [ a, b ] к интегралу.

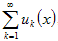Теорема 6. Если все функции uk (x) непрерывны на сегменте [ a, b ] и, то " x, x 0Î [ a, b ]

,

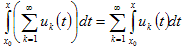то есть при указанных условиях функциональный ряд можно интегрировать почленно.

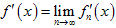Теорема 7. Пусть функции fn (x) имеют непрерывные производные на сегменте [ a, b ].Пусть { fn (x)}→ fn (x)хотя бы в одной точке сегмента [ a, b ], а последовательность производных сходится равномерно на [ a, b ]. Тогда последовательность fn (x) сходится равномерно на сегменте к функции f (x), дифференцируемой на сегменте [ a, b ] и предельная функция f (x) имеет производную. Другими словами,

последовательность можно дифференцировать почленно.

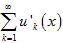Теорема 8. Если все функции uk (x) имеют производную на сегменте [ a, b ] и если ряд

из производных сходится равномерно на сегменте к функции F (x), а сам ряд

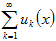
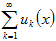сходится хотя бы в одной точке сегмента, то ряд сходится равномерно

на [ a, b ] к функции S (x), S' (x) = F (x). То есть ряд при этих условиях можно дифференцировать почленно.

ГЛАВА XIX. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ. § 3