Предположим, что нам удалось измерить скорости всех молекул газа в некоторый момент времени, т.е. получить v1, v2,...,vN. Нанесем их на ось скоростей в виде точек. Как видно из рис. 8.3, распределение точек на оси не будет равномерным – в области больших и малых скоростей они располагаются сравнительно редко, а большинство из них группируется вблизи некоторого промежуточного значения.
Подсчитаем число молекул dN, скорости которых попадают внутрь интервала скоростей от v до v+dv (рис. 8.3). Очевидно, что dN пропорционально общему числу молекул N и ширине интервала dv. Кроме того, dN зависит от того, у какого значения скорости выбран интервал шириной dv (как видно из рис. 8.3, если продвигать этот интервал, не меняя его ширины, вдоль оси v, то число точек попадающих внутрь этого интервала, будет изменяться). Таким образом, dN пропорционально некоторой функции скоростей f(v). В итоге
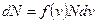 . .
| (8.14) |
Из (8.14) следует
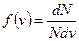 . .
| (8.15) |
Функция f(v) называется функцией распределения молекул по скоростям. Для единичного интервала скоростей 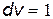 ,
, 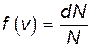 , т.е. функция распределения численно равна доле молекул, скорости которых попадают внутрь единичного интервала скоростей при заданном значении скорости.
, т.е. функция распределения численно равна доле молекул, скорости которых попадают внутрь единичного интервала скоростей при заданном значении скорости.
|
|
|
Явный вид функции распределения был найден Максвеллом в 1860 г.:
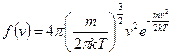 . .
| (8.16) |
График функции f(v) показан на рис. 8.4. С помощью этого графика можно найти относительное число молекул, скорости которых лежат в интервале от v до v+dv. Для этого нужно найти площадь заштрихованной фигуры (рис. 8.4), которую приближенно можно заменить прямоугольником со сторонами f(v) и dv. с учетом (8.15) имеем
площадь = 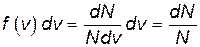 , ,
|
что и требовалось доказать.
Из рис. 8.4 видно, что при той же ширине интервала dv наибольшая площадь получается вблизи скорости, соответствующей максимуму функции распределения. Эта скорость называется наиболее вероятной.
Значение наиболее вероятной скорости можно найти из условия
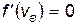 , ,
|
Используя это условие, из (8.16) легко получить
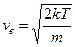 . .
| (8.17) |
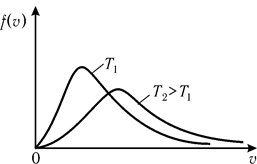 Отметим, что с повышением температуры наиболее вероятная скорость возрастает. Как видно из рис. 8.5, с ростом температуры максимум функции распределения смещается в область больших скоростей; при этом возрастает также доля молекул, обладающих большими значениями скоростей.
Отметим, что с повышением температуры наиболее вероятная скорость возрастает. Как видно из рис. 8.5, с ростом температуры максимум функции распределения смещается в область больших скоростей; при этом возрастает также доля молекул, обладающих большими значениями скоростей.
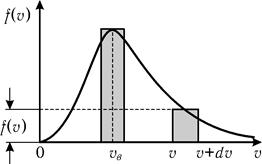
Рис. 8.4. Рис. 8.5.
С помощью функции распределения f(v) можно найти также среднее значение скорости:
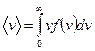 . .
|
Подставив сюда f(v) из (8.16), получим:
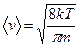 . .
| (8.18) |
Аналогично можно вычислить квадрат среднеквадратичной скорости:
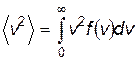 . .
|
Однако проще это сделать, если учесть, что средняя кинетическая энергия хаотического движения молекул
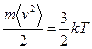 . .
|
Отсюда
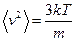 . .
|
или
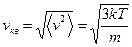 . .
| (8.19) |
Из выражений (8.17) – (8.19) видно, что 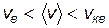 . Отношение этих скоростей
. Отношение этих скоростей
|
|
|
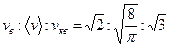 . .
|
Заменим в формулах (8.17) – (8.18) отношение 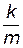 на
на
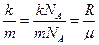 , ,
|
где m – молярная масса (т.е. масса одного моля газа). Тогда формулы (8.17) – (8.18) примут вид, удобный для практических расчетов:
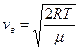 ; ; 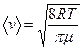 ; ; 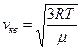 . .
|
 2015-02-04
2015-02-04 507
507








