5.1. Краткие теоретические сведения
5.1.1. Основные понятия и определения
В реальных электрических цепях установившиеся режимы характеризуются периодическими ЭДС и токами, в той или иной мере отличающимися от синусоидальных. В качестве примера можно указать различные схемы выпрямления, регулирования с помощью полупроводниковых преобразователей напряжения на исполнительных механизмах и т.п. Даже в генераторах переменного тока, которые проектируются так, чтобы ЭДС в их обмотках была возможно близка к синусоидальной, напряжение содержит в некоторой мере высшие гармоники, обусловленные конструктивными особенностями генераторов. В самом общем случае имеют дело с периодическими несинусоидальными токами и напряжениями.
Линейные цепи, в которых действуют периодические несинусоидальные ЭДС, могут рассчитываться методом наложения с использованием разложения периодических функций в гармонический ряд.
Как известно из курса математики, любая периодическая функция e (t), удовлетворяющая условиям Дирихле, может быть разложена в ряд Фурье следующего вида
|
|
|
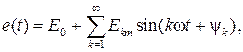
где E 0− постоянная составляющая ЭДС; Ekm− амплитуда и ψ k − начальная фаза k −й гармоники.
Данный ряд содержит бесконечное число гармоник, но, как правило, можно ограничиться некоторым конечным числом членов ряда.
Для вычисления коэффициентов ряда Фурье целесообразно представить его в виде гармонических функций без начальных фаз:
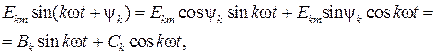
где 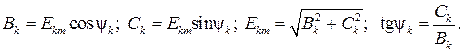
Тогда можно записать
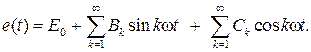 (5.1)
(5.1)
Постоянная составляющая E 0 и коэффициенты Bk и Ck в (5.1) определяются по формулам, которые приводятся в любом справочнике по математике для наиболее распространенных периодических кривых.
Представление ряда Фурье в виде (5.1) удобно в тех случаях, когда по виду кривой несинусоидальной функции можно сразу определить состав гармоник. Например, если кривая e (t) симметрична относительно начала координат, т.е. выполняется условие e (− t)= − e (t), то в разложении (5.1) будут отсутствовать постоянная составляющая и косинусоидальные члены. Если кривая симметрична относительно оси ординат, т.е. выполняется условие e (− t)= e (t), то в разложении (5.1) будут отсутствовать синусоидальные члены.
Для большинства кривых, соответствующих форме реальных негармонических напряжений, в справочниках приводятся формулы разложения в виде ряда (5.1). Если напряжения представляются в виде кривых неправильной формы, то они задаются в виде графиков. Тогда для разложения их в ряд Фурье применяют приближенные формулы, например, формулы Бесселя, которые дают требуемую точность при замене реальной кривой ее представлением гармоническим рядом.
|
|
|
В нашу задачу не входит изложение теории представления функций в виде гармонических рядов. Поэтому в дальнейшем будем считать, что в случае негармонических периодических ЭДС и напряжений их гармонический состав известен.
В соответствии с принципом наложения для линейных цепей каждому мгновенному значению ЭДС или напряжению гармонического ряда
e=e 0+ e 1 +e 2+ e 3+...
u=u 0+ u 1 +u 2+ u 3+... (5.2)
соответствует свой ток:
i=i 0+ i 1+ i 2+ i 3+.... (5.3)
Так как каждая составляющая тока является либо постоянной величиной, либо синусоидальной функцией времени, то для расчета каждой из них в отдельности могут быть применены методы расчета, рассмотренные в разделах 1 и 2 настоящего пособия. В частности, целесообразно использовать метод комплексных амплитуд. При этом следует иметь ввиду, что суммировать полученные комплексы токов для отдельных гармоник нельзя, т.к. они имеют разные частоты. Поэтому суммировать можно лишь мгновенные значения, выраженные как функции времени.
Действующее значение периодического тока I определяется как среднее квадратичное значение за период T:
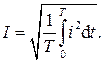
Опуская математические выкладки, для действующего значения периодического тока, представленного в виде гармонического ряда (5.3), получим:
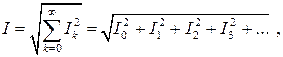 (5.4)
(5.4)
т.е. действующее значение периодического несинусоидального тока равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений всех гармоник.
Аналогично получаем для действующих значений периодических несинусоидальных ЭДС и напряжений:
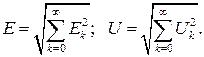 (5.5)
(5.5)
Измерительные приборы электромагнитной, тепловой и электродинамической систем показывают действующие значения измеряемых величин. Приборы магнитоэлектрической системы показывают среднее значение тока или напряжения за период, т.е. постоянную составляющую ряда Фурье:
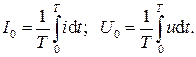
Для схем выпрямления переменного напряжения основной задачей является получение в идеальном случае постоянного напряжения. Тем не менее, в реальных схемах выходное напряжение содержит высшие гармоники. Оценку пульсаций выходного напряжения и тока можно оценить коэффициентом, представляющим собой отношение действующего значения выпрямленного напряжения или тока к его среднему по модулю значению:
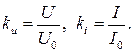 (5.6)
(5.6)
Активная мощность в цепях несинусоидального тока определяется как среднее значение мгновенной мощности за период T:

Подставляя в последнее выражение мгновенные напряжения и токи в виде гармонических рядов (5.2) и (5.3) и опуская тождественные преобразования, получим:
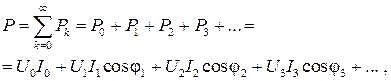
где φ i − фазовый сдвиг тока и напряжения для соответствующей гармоники.
Таким образом, активная мощность при периодических несинусоидальных токах и напряжениях равна сумме активных мощностей постоянных и всех гармонических составляющих тока и напряжения.
При периодических несинусоидальных токах и напряжениях, как и при синусоидальных, вводят понятие о коэффициенте мощности, обозначая его через α:
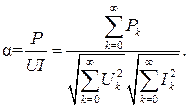
Величина α равна единице только в том случае, если цепь обладает только активным сопротивлением, не зависящим от частоты. Во всех остальных случаях α˂1.
5.1.2. Расчет цепей негармонического тока
Расчет цепей при периодических негармонических ЭДС и токах ведется по методу наложения. Последовательность расчета рассмотрим на примере цепи со смешанным соединением элементов R, L, C (рис. 5.1,а) и с источником, ЭДС e (t) которого изменяется по закону, соответствующему однополупериодному выпрямлению синусоидального напряжения с амплитудой Em (рис. 5.1,б):
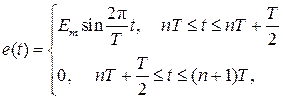
где n = 0,±1,±2,±3,...; T − период.
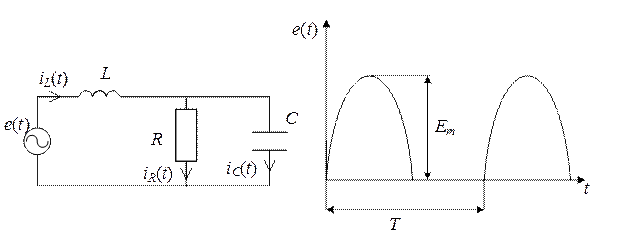
а) б)
Рис. 5.1. Цепь с негармоническим источником:
а) схема цепи; б) кривая ЭДС
Разложение несинусоидальной ЭДС в гармонический ряд имеет вид:
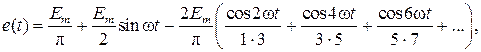 (5.7)
(5.7)
где 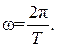
Какие члены в разложении учитывать при расчетах, определяется требуемой точностью. Кроме того, ряд, как правило, быстро убывает. Начиная с четвертого члена ряда, амплитуда гармоник составляет менее 5-10% от амплитуды первой гармоники. Поэтому для иллюстрации метода расчета рассмотрим только первые три члена ряда:
|
|
|
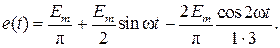
Как следует из последнего выражения, ЭДС или напряжение источника представляет собой совокупность ЭДС или напряжений трех источников: одного постоянного, величиной 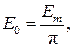 и двух гармонических:
и двух гармонических:
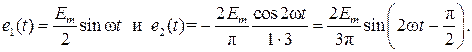
Гармонические ЭДС e 1(t) и e 2(t) называют соответственно первой и второй гармониками, а напряжение постоянного источника − постоянной составляющей ЭДС.
В соответствии с методом наложения необходимо произвести расчет цепи при каждом из воздействий. При этом для постоянной составляющей цепь следует рассматривать как цепь постоянного тока, а для гармоник − как цепь гармонического тока соответствующей частоты.
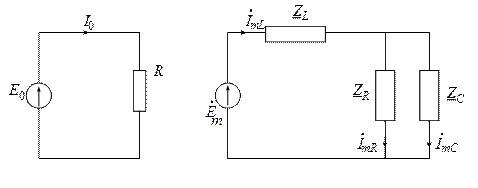
Таким образом, принципиально рассматриваются две схемы цепи: постоянного и переменного тока. Применительно к исходной цепи (рис. 5.1,а) они имеют вид, как на рис. 5.2.
а) б)
Рис. 5.2. Расчетные схемы: а) для постоянной составляющей;
б) для гармонических составляющих
Цепь на рис. 5.2,а не содержит индуктивности и емкости, поскольку в установившемся режиме в цепи постоянного тока индуктивность эквивалентна сопротивлению с нулевым сопротивлением, а емкость эквивалентна разрыву цепи.
Цепь на рис. 5.2,б представляет собой изображение исходной цепи в комплексной области, поскольку расчет цепей гармонического тока ведется символическим методом. При этом для первой гармоники:
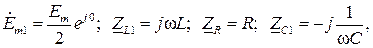
и для второй гармоники:
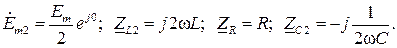
Расчет цепи как для постоянной составляющей, так и для гармоник ведется известными методами, изложенными в разделах 1 и 2 пособия, поэтому приведем только в общем виде выражения для токов в ветвях для каждой составляющей ЭДС:
− для постоянной составляющей 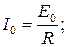
− для первой гармоники
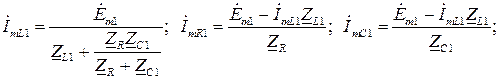
− для второй гармоники
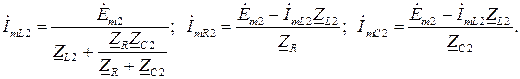
Переходя от комплексных амплитуд токов в ветвях к временным функциям, получим выражения для мгновенных токов в ветвях схемы:
|
|
|
− для первой гармоники:
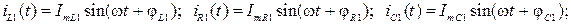
− для второй гармоники:
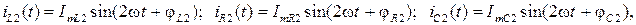 где под начальными фазами гармонических функций (φ) понимаются аргументы соответствующих комплексных амплитуд токов.
где под начальными фазами гармонических функций (φ) понимаются аргументы соответствующих комплексных амплитуд токов.
Окончательно токи в ветвях при действии негармонической ЭДС будут представлять собой суммы соответствующих мгновенных токов:
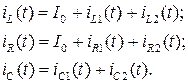
Для построения графиков токов в ветвях необходимо сложить ординаты постоянной составляющей и мгновенных значений всех рассчитанных гармоник.
5.2. Лабораторная работа №9
 2015-02-18
2015-02-18 4888
4888








