Вывод: все мои мечты сбылись

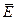
Представим все высказывания в дизъюнктивной форме.

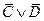
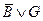
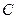
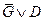
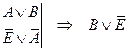
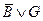
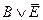
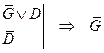
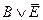
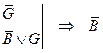
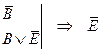- что и требовалось доказать

Задача 2. Сформулировать представленную выше задачу на языке логики предикатов и упростить полученную систему используя теоремы и тождества логики предикатов.

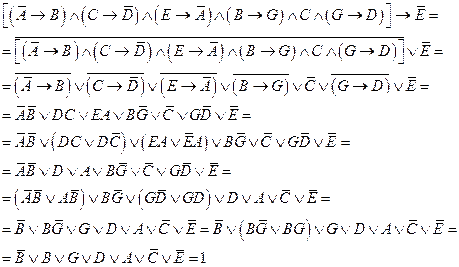
Тождество доказано.

Задача 3. Сконструировать машину Тьюринга (написать соответствующую программу) для решения следующей задачи.

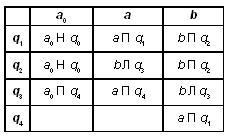
Дана строка из букв “ a ” и “ b ”. Разработать машину Тьюринга, которая переместит все буквы “ a ” в левую, а буквы “ b ” — в правую части строки. Автомат в состоянии q 1 обозревает крайний левый символ строки. Кроме самой программы-таблицы, описать словами, что выполняется машиной в каждом состоянии.

Машина Тьюринга должна “понимать”, по цепочке каких букв она идет, т.е. у нее должно быть как минимум два состояния. Пусть состояние q₁ — движение по цепочке из букв “a”, а q₂ — состояние движения по цепочке из букв “b”. Заметим, что цепочка может состоять и из одной буквы. Если мы дошли до конца строки в состоянии q₁ или q₂, т.е. встретили a₀, машина должна остановиться, мы обработали всю строку.

Рассмотрим следующие варианты входных слов:

bba —> abb

bbbaab —> aabbbb

aabbbaab —> aaaabbbb

Первый вариант входного слова можно последовательно обработать следующим образом: bba —> bbb —> вернуться к левому концу цепочки из букв “b” —> abb (заменить первую букву в этой цепочке на “a”). Для выполнения этих действий нам потребуется ввести два новых состояния и, кроме того, уточнить состояние q₂. Таким образом, для решения этой задачи нам нужно построить машину Тьюринга со следующими состояниями:

q₁ — идем вправо по цепочке букв “a”. Если цепочка заканчивается a₀, то переходим вq₀; если заканчивается буквой “b”, то переходим в q₂;

q₂ — идем вправо по цепочке букв “b”, если цепочка заканчивается a₀, то переходим вq₀; если заканчивается “a”, то заменяем букву “a” на “b”, переходим в состояние q₃(цепочку вида 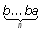заменили на цепочку вида );

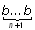q₃ — идем влево по цепочке букв “b” до ее левого конца. Если встретили a₀ или “a”, то переходим в q₄;

q₄ — заменяем “b” на “a” и переходим в q₁ (цепочку вида 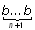заменяем на цепочку вида .

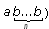Задача 4. Записать логическую функцию, соответствующую высказыванию:

«Если прогноз показывает, что можно получить крупную прибыль на выпуске новых товаров (A), то при разработке стратегии развития фирме следует сделать упор на маркетинг (B) и сеть распределения (C), а также целесообразно открыть более крупные магазины (D) и расширить торговую сеть (E)».

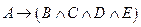
Задача 5. Записать сложное высказывание «Если рабочий отсутствовал на работе (A), он не выполнил задания (B). Иванов присутствовал на работе, следовательно, он не выполнил задания» логической формулой и минимизировать его, используя карту Карно.

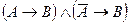
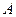
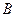
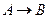
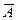
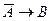
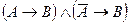
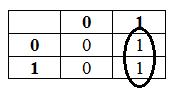
В нашем случае не меняется переменная 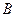, значит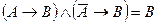

Задача 6. Каждой пропозициональной форме, содержащей n различных пропозициональных букв, соответствует таблица истинности с 2ⁿ строками.

Составить таблицу истинности для следующей формы: (((С & D) V (А & В)) → (В V (В)))

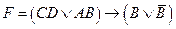
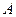
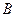
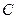
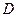
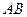
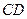
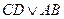
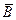
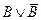
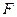
Задача 7. Составить рекуррентное выражение для вычисления функции f(n) = х + у² (рекурсия проводится по переменной y), представив функции h(х, у, m) и g(х, у).

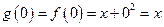
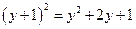
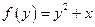
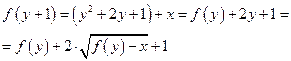
Тогда

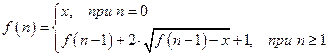
Задача 8. Представить на языке ГСА (операторные вершины обозначить буквами А1, А2, …, Аn, а логические – буквами α1, α2, …, αm), используя рекомендуемые ГОСТом обозначения, алгоритм решения следующей задачи.

Из четырех представленных чисел A, B, C и D, не используя понятие массива, составить невозрастающую последовательность.

Введем обозначения:

A0 – «начало»

А1 – «x1 = A»

А2 – «x1 = B; x2 = A»

А3 – «x2 = B»

А4 – «x3 = x2; x2 = x1; x1 = C»

А5 – «x3 = x2; x2 = C»

А6 – «x3 = C»

А7 – «x4 = x3; x3 = x2; x2 = x1; x1 = D»

А8 – «x4 = x3; x3 = x2; x2 = D»

А9 – «x4 = x3; x3 = D»

А10 – «x4 = C»

А11 – «конец»

α1 – «B > x1»

α2 – «C > x2»

α3 – «C > x1»

α4 – «D > x3»

α5 – «D > x1»

α6 – «D > x2»

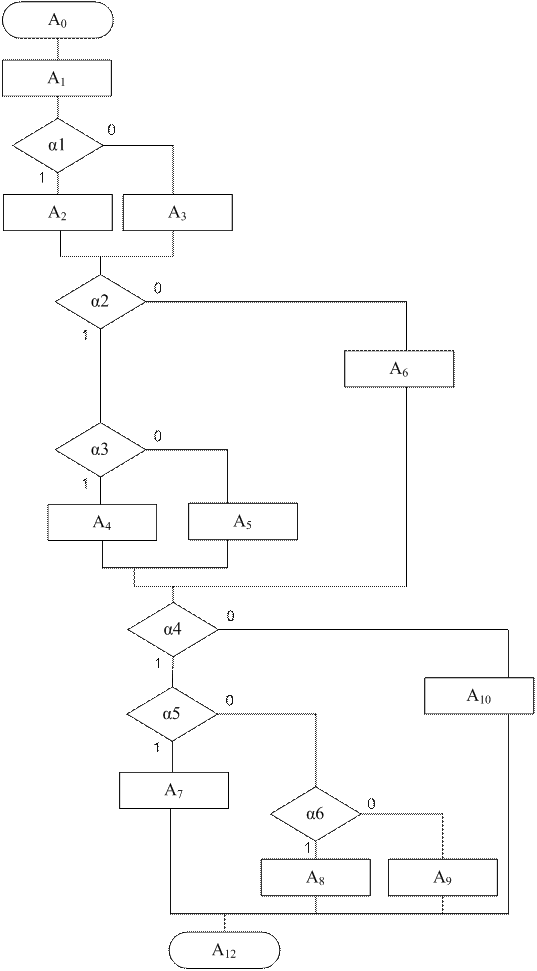
Задача 9. Представленный в предыдущем задании алгоритм перевести с языка ГСА на язык ЛСА (используя обозначения предыдущей задачи).

A₀A₁α₁↑¹A₂↑²↑↓¹A₃↓²α₂↑³α₃↑⁴A₄0↑⁵↓⁴A₅0↑⁶↓³A₆↓⁵↓⁶α₄↑⁷α₅↑⁸A₇0↑⁹↓⁸α₆↑¹⁰A₈↑¹¹↓¹⁰A₉↑¹²↓⁷A₁₀↓¹²↓¹¹↓⁹A₁₁

Библиографический список

1. Игошин В.И. Задачи и модели по математической логике и теории алгоритмов. – 2-е изд. – М.: Академия, 2006. – 304 с.

2. Тимофеева, И.Л. Математическая логика: курс лекций: учеб. пособие. – 2-е изд. – М.: КДУ, 2007.

3. Гладкий А.В. Математическая логика и теория алгоритмов. – М.: МЦНМО, 2001.

4. Зюзьков В.М, Шелупанов А.А. Математическая логика и теория алгоритмов: Учебное пособие для вузов. – 2-е изд. – М.: Горячая линия–Телеком, 2007. – 176 с.

5. Игошин В.И. Задачник-практикум по математической логике: уч. пособие. – М.: Академия, 2006.

6. Галиев Ш.И. Математическая логика и теория алгоритмов. – Казань: Издательство КГТУ им. А.Н. Туполева. 2002. – 270 с.