- Итерация
 1.
1. 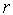 =1 ТИН1=[
=1 ТИН1=[ 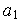 ,
, 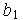 ]=[
]=[ 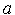 ,
, 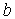 ]=[0,13]:
]=[0,13]:
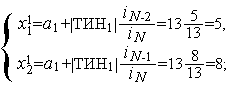
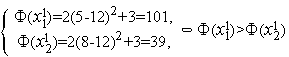 .
. -
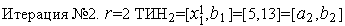 :
:
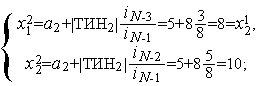
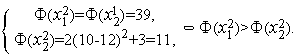
-
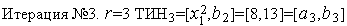 :
:
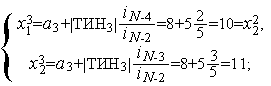
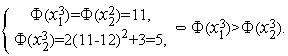
-
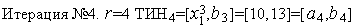 :
:
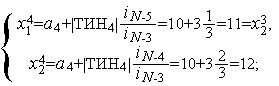
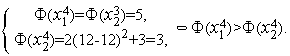
-
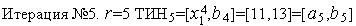 :
:
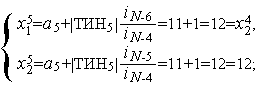
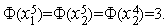
- Итерация
 6.
6. 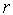 =6 ТИН5=ТИН6=[11,13]:
=6 ТИН5=ТИН6=[11,13]:
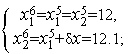
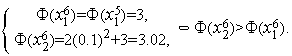
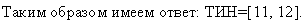
4.4 Алгоритм золотого сечения
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции  (
( ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 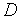 =[
=[ 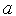 ,
, 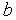 ],
],
 (
( )=
)=  (
(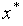 ).
).
Свойства золотого сечения.
Рассмотрим интервал [ 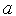 ,
, 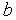 ] (см. рис. 1). Говорят, что точка c выполняет золотое сечение интервала [
] (см. рис. 1). Говорят, что точка c выполняет золотое сечение интервала [ 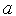 ,
, 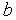 ], если
], если
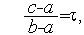 | (1) |
где 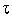 =
= 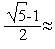 0,618- решение квадратного уравнения
0,618- решение квадратного уравнения
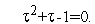 | (2) |
 |
Рис. 1. К определению золотого сечения отрезка.
Из определения золотого сечения следует, что 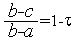 . Действительно,
. Действительно,
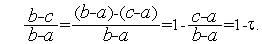
Алгоритм золотого сечения.
Алгоритм золотого сечения относится к классу последовательных методов поиска.
1. Выполняем присваивания 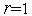 ,
, 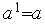 ,
, 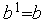 ,
, 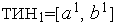 .
.
2. Вычисляем величины (см. Рис. 2)
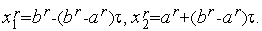 | (3) |
3.
4. Вычисляем значения 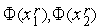 функции
функции 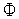 (
( ).
).
5. Если 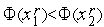 , то выполняем присваивания
, то выполняем присваивания 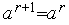 ,
, 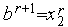 ,
, 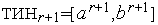 . Иначе - выполняем присваивания
. Иначе - выполняем присваивания 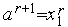 ,
, 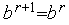 ,
, 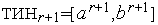
6. Если 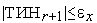 , то заканчиваем вычисления. Иначе - выполняем присваивание
, то заканчиваем вычисления. Иначе - выполняем присваивание  =
=  +1 и переходим на п.2. Здесь
+1 и переходим на п.2. Здесь 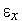 – требуемая точность решения
– требуемая точность решения 
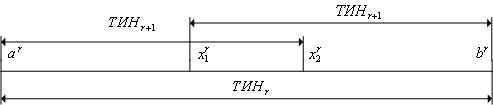 |
Рис. 2. К определению величин x 1 r, x 2 r.
В качестве приближенного значения точки минимума 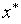 с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
Некоторые свойства алгоритм золотого сечения.
Утверждение 1. Точки 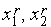 расположены симметрично относительно концов текущего интервала неопределенности.
расположены симметрично относительно концов текущего интервала неопределенности.
Действительно, из (3) следует, что точка 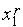 отстоит от точки
отстоит от точки 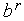 на величину
на величину 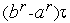 ; точка
; точка 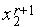 отстоит от точки
отстоит от точки 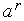 на ту же величину
на ту же величину 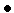
Утверждение 2. Для любого 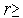 1 алгоритм золотого сечения обладает следующим свойством: одна из точек
1 алгоритм золотого сечения обладает следующим свойством: одна из точек 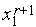 ,
, 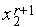 совпадает с одной из точек
совпадает с одной из точек 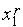 ,
, 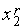 .
.
Доказательство. Пусть на  -й итерации
-й итерации 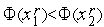 . В соответствии с алгоритмом золотого сечения
. В соответствии с алгоритмом золотого сечения 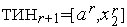 причем, очевидно,
причем, очевидно, 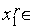 ТИН r +1. Для того, чтобы доказать справедливость утверждения достаточно показать, что верно отношение
ТИН r +1. Для того, чтобы доказать справедливость утверждения достаточно показать, что верно отношение
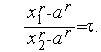 | (4) |
Из соотношений (3) следует, что
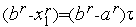
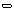
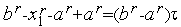
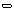
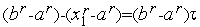
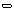
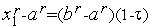 .
.
Аналогично имеем 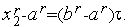
Разделив первый из этих результатов на второй, получим
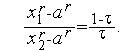 | (5) |
Из уравнения (2) следует, что 1- 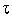 =
= 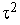 . Отсюда и из (5) следует справедливость (4).
. Отсюда и из (5) следует справедливость (4).
Аналогично проводится доказательство для случая 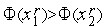
Указанное свойство алгоритма золотого сечения позволяет на каждой итерации (кроме первой) производить испытания только в одной точке.
Из схемы алгоритма золотого сечения имеем.
Утверждение 3. В результате одной итерации алгоритма золотого сечения длина текущего интервала неопределенности сокращается в 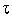 раз
раз 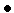
Поэтому количество итераций 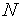 , необходимых для нахождения минимума функции с точностью
, необходимых для нахождения минимума функции с точностью 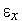 , находится из условия
, находится из условия
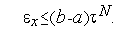
Из утверждения 3 и результатов предыдущего параграфа следует, что при достаточно больших 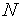 алгоритм Фибоначчи практически идентичен алгоритму золотого сечения.
алгоритм Фибоначчи практически идентичен алгоритму золотого сечения.
4.5 Сравнение эффективности алгоритмов одномерной условной оптимизации
Аналитическое вычисление критерия качества алгоритмов оптимизации удается только для следующей одномерной задачи условной оптимизации: найти минимум одномерной унимодальной функции  (
( ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 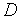 =[
=[ 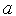 ,
, 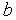 ],
],
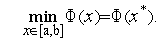 | (1) |
Обозначим через 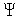 класс одномерных унимодальных функций. Пусть множество рассматриваемых алгоритмов решения задачи (1) есть
класс одномерных унимодальных функций. Пусть множество рассматриваемых алгоритмов решения задачи (1) есть 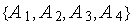 , где
, где
-
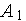 - алгоритм равномерного поиска,
- алгоритм равномерного поиска, -
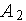 - алгоритм равномерного дихотомического поиска,
- алгоритм равномерного дихотомического поиска, -
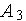 - алгоритм Фибоначчи,
- алгоритм Фибоначчи, -
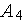 - алгоритм золотого сечения.
- алгоритм золотого сечения.
В качестве критерия оптимальности алгоритмов 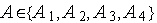 на классе функций
на классе функций 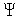 используем максимальную длину текущего интервала неопределенности после
используем максимальную длину текущего интервала неопределенности после 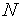 испытаний
испытаний
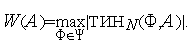
В параграфе 1 мы показали, что если количество узлов сетки равно 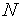 +1, то после одной итерации алгоритма равномерного поиска текущий интервал неопределенности уменьшается в
+1, то после одной итерации алгоритма равномерного поиска текущий интервал неопределенности уменьшается в 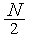 раз. Поэтому
раз. Поэтому
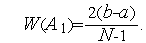
Из результатов параграфа 2 следует, что после одной итерации (двух испытаний) алгоритма равномерного поиска текущий интервал неопределенности уменьшается в 2 раза. Поэтому
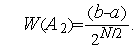
В параграфе 3 показано, что в результате 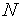 итераций (
итераций (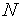 +1 испытаний) алгоритма Фибоначчи длина текущего интервала неопределенности становится равной
+1 испытаний) алгоритма Фибоначчи длина текущего интервала неопределенности становится равной 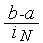 . Отсюда следует, что
. Отсюда следует, что
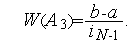
Наконец, в параграфе 4 показано, что в результате 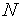 итерации (
итерации (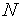 +1 испытаний) алгоритма золотого сечения длина текущего интервала неопределенности становится равной (
+1 испытаний) алгоритма золотого сечения длина текущего интервала неопределенности становится равной (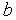 -
- 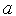 )
) 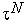 . Поэтому
. Поэтому
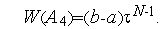
Сравним эффективности алгоритма деления пополам и алгоритма Фибоначчи при 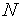 =14:
=14:
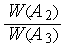 =
= 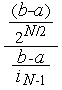 =
= 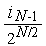 =
= 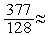 3.
3.
Таким образом, при 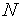 =14 алгоритм Фибоначчи почти в 3 раз эффективнее алгоритма деления пополам.
=14 алгоритм Фибоначчи почти в 3 раз эффективнее алгоритма деления пополам.
При 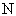 =14 сравним также эффективности алгоритма Фибоначчи и алгоритма золотого сечения:
=14 сравним также эффективности алгоритма Фибоначчи и алгоритма золотого сечения:
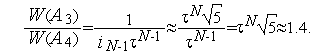
Здесь учтено, что 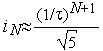 .
.
Таким образом, при 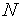 =14 алгоритм золотого сечения примерно на 40 процентов эффективнее алгоритма Фибоначчи.
=14 алгоритм золотого сечения примерно на 40 процентов эффективнее алгоритма Фибоначчи.
4.6 Метод квадратичной аппроксимации
Метод квадратичной аппроксимации относится к семейству методов полиномиальной аппроксимации. Идея метода полиномиальной аппроксимации состоит в том, что в некоторой окрестности минимума функции  (
( ) она аппроксимируется полиномом достаточно высокого порядка и в качестве точки минимума функции
) она аппроксимируется полиномом достаточно высокого порядка и в качестве точки минимума функции  (
( ) (или в качестве очередного приближения к этой точке) принимается точка минимума аппроксимирующего полинома. В силу того, что аппроксимирующая функция является полиномом, этот минимум находится легко.
) (или в качестве очередного приближения к этой точке) принимается точка минимума аппроксимирующего полинома. В силу того, что аппроксимирующая функция является полиномом, этот минимум находится легко.
В качестве аппроксимирующих полиномов чаще всего используются полиномы второго и третьего порядков, т.е. квадратичная и кубическая аппроксимации.
Квадратичная аппроксимация.
Рассмотрим квадратичную аппроксимацию (см. рис. 1). Пусть в процессе решения задачи поиска минимума функции  (
( ) тем или иным образом получены попарно не совпадающие точки
) тем или иным образом получены попарно не совпадающие точки 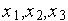 , принадлежащие области допустимых значений
, принадлежащие области допустимых значений 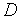 (не обязательно упорядоченные слева направо!).
(не обязательно упорядоченные слева направо!).
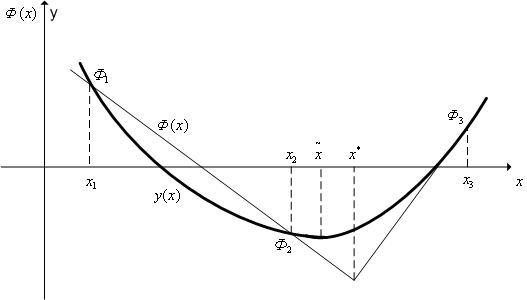 |
Рис. 1. Квадратичная аппроксимация.
Построим квадратичную функцию
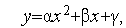 | (1) |
проходящую через точки 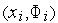 ,
, 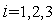 , где
, где 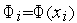 .
.
Коэффициенты 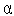 ,
, 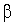 ,
, 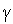 функции (1) удовлетворяют системе линейных алгебраических уравнений (СЛАУ)
функции (1) удовлетворяют системе линейных алгебраических уравнений (СЛАУ)
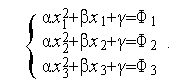 | (2) |
Определитель СЛАУ (2) является определителем Вандермонда, который отличен от нуля, если величины 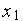 ,
, 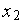 ,
, 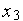 попарно различны.
попарно различны.
Таким образом, в сделанных предположениях СЛАУ (2) имеет решение и, притом единственное. Поскольку определитель СЛАУ (2) равен 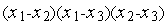 , это решение имеет вид
, это решение имеет вид
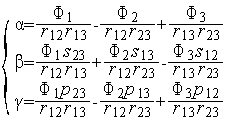 ,
,
где 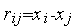 ,
, 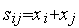 ,
,  .
.
Подставим найденные значения коэффициентов 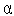 ,
, 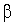 ,
, 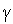 в необходимое условие
в необходимое условие 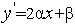 =0 минимума квадратичной функции (1), получим стационарную точку этой функции
=0 минимума квадратичной функции (1), получим стационарную точку этой функции
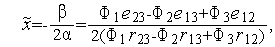 | (3) |
где 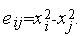
Метод квадратичной аппроксимации.
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции  (
( ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 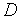 =[
=[ 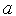 ,
, 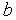 ],
],
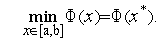 | (4) |
Метод квадратичной аппроксимации относится к классу методов сокращения текущего интервала неопределенности. Пусть при решении задачи (4) каким-либо методом получены три точки 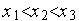 , принадлежащие области допустимых значений, такие, что
, принадлежащие области допустимых значений, такие, что 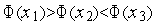 .
.
Схема метода квадратичной аппроксимации:
1. Выполняем присваивания 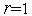 ,
, 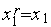 ,
, 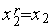 ,
, 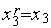 ,
, 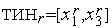 .
.
2. Вычисляем значения 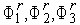 функции
функции 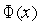 в точках
в точках 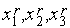 , соответственно.
, соответственно.
3. По формуле (3) вычисляем величину 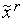 и находим значение функции
и находим значение функции  (
( ) в этой точке
) в этой точке 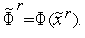
4. Находим следующие три точки:
o случай (а) - если 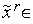 [
[ 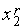 ,
, 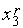 ], то
], то 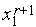 =
= 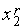 ,
, 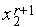 =
= 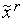 ,
, 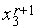 =
= 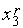 (см. рис. 2);
(см. рис. 2);
o случай (б) - если 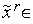 [
[ 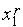 ,
, 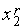 ], то
], то 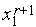 =
= 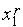 ,
, 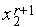 =
= 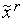 ,
, 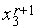 =
= 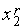 (см. рис. 3).
(см. рис. 3).
5. В качестве следующего текущего интервала неопределенности принимаем 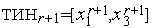 .
.
6. Если 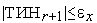 , то заканчиваем вычисления. Иначе - выполняем присваивание
, то заканчиваем вычисления. Иначе - выполняем присваивание  =
=  +1 и переходим на п.2. Здесь
+1 и переходим на п.2. Здесь 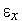 – требуемая точность решения
– требуемая точность решения 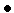
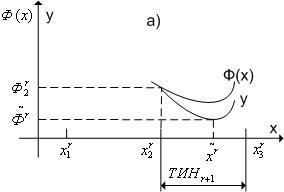 |
Рис. 2. К методу квадратичной аппроксимации (случай а).
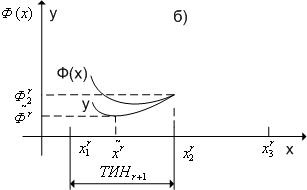 |
Рис. 3. К методу квадратичной аппроксимации (случай б).
В качестве приближенного значения точки минимума 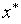 с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
Замечание. В силу условий 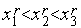 ,
, 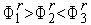 точка
точка 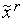 всегда принадлежит текущему интервалу неопределенности ТИН r =[
всегда принадлежит текущему интервалу неопределенности ТИН r =[ 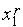 ,
, 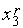 ]
] 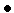
4.7 Метод Паулла
Напомним, что методы, использующие квадратичную аппроксимацию, относятся к семейству методов полиномиальной аппроксимации.
В параграфе 6 показано, что если имеются попарно не совпадающие точки 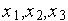 и соответствующие значения
и соответствующие значения 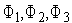 минимизируемой функции, то аппроксимирующий квадратичный полином
минимизируемой функции, то аппроксимирующий квадратичный полином 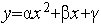 достигает минимального значения в точке
достигает минимального значения в точке
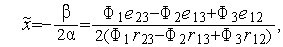 | (1) |
где 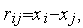
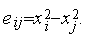
Рассмотрим следующую задачу безусловной оптимизации: найти минимум одномерной унимодальной функции  (
( ), определенной в незамкнутой области допустимых значений
), определенной в незамкнутой области допустимых значений 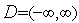 ,
,
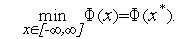 | (2) |
Метод Паулла решения задачи (2) может быть весьма полезен при решении задач безусловной оптимизации многопараметрических функций (см. далее).
Схема метода Паулла:
1. Полагаем  =1 и задаем начальную точку
=1 и задаем начальную точку 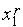 .
.
2. Находим точку 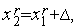 где Δ – длина шага, которая должна быть величиной того же порядка, что и расстояние точки
где Δ – длина шага, которая должна быть величиной того же порядка, что и расстояние точки 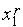 до точки минимума функции
до точки минимума функции  (
( ) (оценка этого расстояния является самостоятельной проблемой).
) (оценка этого расстояния является самостоятельной проблемой).
3. Вычисляем значения 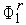 ,
, 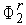 функции
функции  (
( ) в точках
) в точках 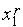 ,
, 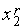 .
.
4. Находим точку 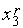 :
:
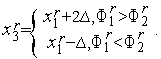
5. Вычисляем значение 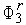 функции
функции  (
( ) в точке
) в точке 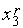 (см. рис. 1).
(см. рис. 1).
6. По формуле (1) вычисляем величину 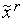 и находим значение функции
и находим значение функции  (
( ) в этой точке
) в этой точке 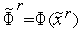 .
.
7. Находим следующие три точки:
o а) если 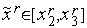 , то
, то 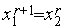 ,
, 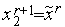 ,
, 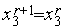 ;
;
o б) если 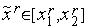 , то
, то 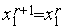 ,
, 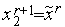 ,
, 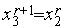 ;
;
o в) если 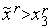 , то
, то 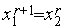 ,
, 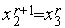 ,
, 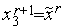 (см. рис. 2);
(см. рис. 2);
o г) если 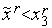 , то
, то 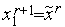 ,
, 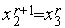 ,
, 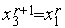 (см. рис. 3).
(см. рис. 3).
8. В качестве следующего текущего интервала неопределенности принимаем 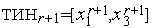 .
.
9. Если 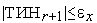 , то заканчиваем вычисления. Иначе - выполняем присваивание
, то заканчиваем вычисления. Иначе - выполняем присваивание  =
=  +1 и переходим на п.6. Здесь
+1 и переходим на п.6. Здесь 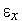 – требуемая точность решения
– требуемая точность решения
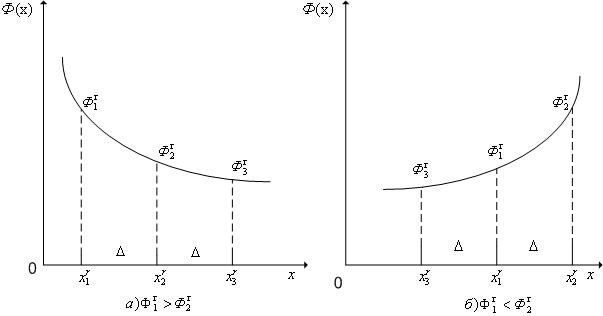 |
Рис. 1. К определению точки x 3r.
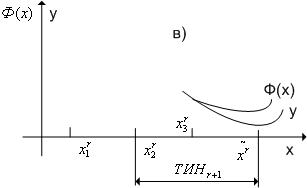 |
Рис. 2. Случай x~r> x 3 r.
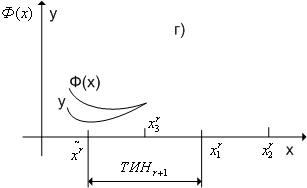 |
Рис. 3. Случай x~r< x 3 r
В качестве приближенного значения точки минимума 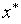 с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
с равными основаниями может быть принята любая точка последнего текущего интервала неопределенности.
Рассмотренный метод Паулла может быть модифицирован и для замкнутой области допустимых значений 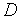 :
:
4.8 Методы на основе поиска стационарной точки критерия оптимальности
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции  (
( ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 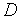 =[
=[ 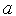 ,
, 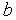 ],
],
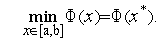 | (1) |
В параграфе 2.1 мы показали, что в этих предположениях необходимым условием минимума функции  (
( ) является условие
) является условие
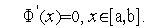 | (2) |
Рассматриваемые в данном параграфе методы первого порядка решения задачи (1) основаны на поиске стационарной точки функции  (
( ), т.е. на решении задачи (2), которая представляет собой задачу нахождения корней функции
), т.е. на решении задачи (2), которая представляет собой задачу нахождения корней функции 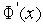 , принадлежащих интервалу [
, принадлежащих интервалу [ 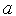 ,
, 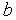 ].
].
Аналитическое решение задачи (2) возможно лишь в простейших случаях. Обычно для решения этой задачи приходится использовать численные методы нахождения корней нелинейных уравнений.
Широко известны следующие методы нахождения корней нелинейных уравнений:
- метод хорд (метод секущих);
- метод касательных (метод Ньютона решения нелинейных уравнений)
Поиск стационарной точки минимизируемой функции методом хорд.
Метод хорд ориентирован на нахождение корня уравнения (2) в случае, когда на границах интервала [ 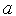 ,
, 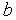 ] знаки производной
] знаки производной 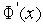 различны. Такая ситуация, очевидно, возможна, если точка минимума функции
различны. Такая ситуация, очевидно, возможна, если точка минимума функции 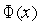 является внутренней точкой интервала [
является внутренней точкой интервала [ 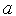 ,
, 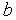 ] — см.рис. 1.
] — см.рис. 1.
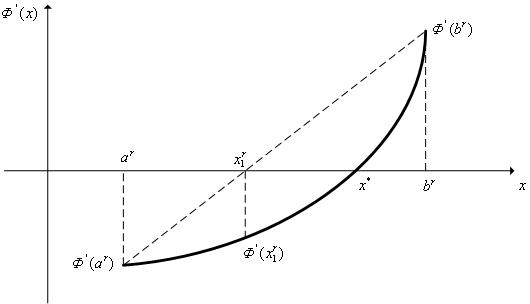 |
Рис. 1. К схеме метода хорд.
Нам далее понадобится значение 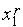 . Из подобия треугольника
. Из подобия треугольника 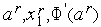 и треугольника
и треугольника 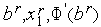 имеем
имеем
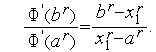
Отсюда следует, что
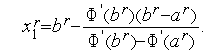 | (3) |
Схема поиска стационарной точки минимизируемой функции методом хорд (см. рис. 1):
1. Выполняем присваивания  =1,
=1, 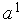 =
= 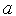 ,
, 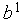 =
= 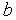 .
.
2. Вычисляем значения производных 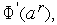
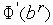 .
.
3. Если производные 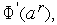
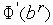 имеют одинаковые знаки – завершаем вычисления (точки
имеют одинаковые знаки – завершаем вычисления (точки 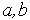 выбраны неверно).
выбраны неверно).
4. По формуле (3) вычисляем приближение 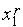 к стационарной точке функции
к стационарной точке функции  (
( ) b значение производной
) b значение производной 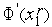 .
.
5. Если 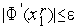 , где
, где 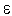 – требуемая точность решения, то принимаем
– требуемая точность решения, то принимаем 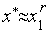 и заканчиваем вычисления.
и заканчиваем вычисления.
6. Если производные 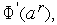
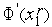 имеют разные знаки, то выполняем присваивания
имеют разные знаки, то выполняем присваивания 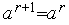 ,
, 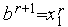 ,
, 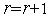 и переходим на п.4.
и переходим на п.4.
7. Если производные 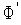 (
(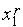 ),
), 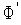 (
(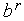 ) имеют разные знаки (как на рис. 1), то выполняем присваивания.
) имеют разные знаки (как на рис. 1), то выполняем присваивания. 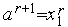 ,
, 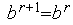 ,
, 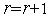 и переходим на п.4
и переходим на п.4 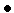
В случае квадратичной функции  (
( ) производная этой функции
) производная этой функции 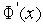 линейна. Поэтому метод хорд гарантирует нахождение стационарной точки функции
линейна. Поэтому метод хорд гарантирует нахождение стационарной точки функции  (
( ) всего за одну итерацию.
) всего за одну итерацию.
Поскольку поиск заканчивается при выполнении условия 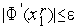 , возможно появление ложных корней. Например, для уравнения
, возможно появление ложных корней. Например, для уравнения 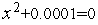 ложный корень
ложный корень 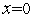 появляется в том случае, если
появляется в том случае, если 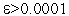 . В подобных случаях увеличивая точность поиска, можно избавить от ложных корней. Однако, возможны уравнения, для которых такой подход не приводит к успеху. Например, уравнение
. В подобных случаях увеличивая точность поиска, можно избавить от ложных корней. Однако, возможны уравнения, для которых такой подход не приводит к успеху. Например, уравнение 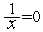 не имеет действительных корней, однако для сколь угодно малого
не имеет действительных корней, однако для сколь угодно малого 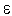 найдется точка, удовлетворяющая условию окончания поиска.
найдется точка, удовлетворяющая условию окончания поиска.
Возможна модификация метода хорд, когда значения производной 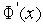 вычисляются приближенно с использованием первых разностей. В этом случае, очевидно, метод становится прямым (нулевого порядка).
вычисляются приближенно с использованием первых разностей. В этом случае, очевидно, метод становится прямым (нулевого порядка).
Поиск стационарной точки минимизируемой функции методом касательных.
Метод касательных ориентирован на нахождение корня уравнения (2) в случае, когда на границах интервала [ 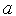 ,
, 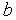 ] знаки производной
] знаки производной 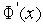 различны. Такая ситуация, очевидно, возможна, если точка минимума функции
различны. Такая ситуация, очевидно, возможна, если точка минимума функции 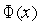 является внутренней точкой интервала [
является внутренней точкой интервала [ 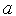 ,
, 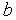 ] — см. рис. 2. метод требует, чтобы функция
] — см. рис. 2. метод требует, чтобы функция  (
( ) была определена и дважды дифференцируема в области допустимых значений
) была определена и дважды дифференцируема в области допустимых значений 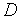 =[
=[ 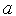 ,
, 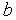 ].
].
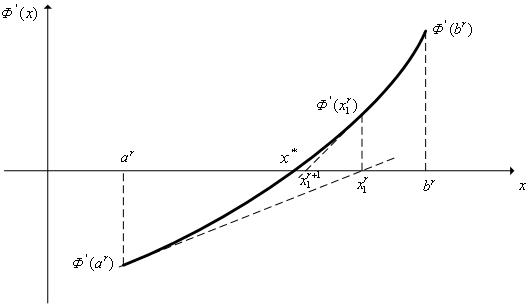 |
Рис. 2. К схеме метода касательных.
Нам далее понадобится значение 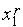 . Линейная функция, аппроксимирующая функцию
. Линейная функция, аппроксимирующая функцию 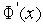 в точке
в точке 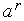 , записывается в виде
, записывается в виде
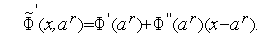 | (4) |
Приравняв правую часть уравнения (4) к нулю, получим
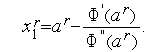 | (5) |
Схема поиска стационарной точки минимизируемой функции методом касательных (см. рис. 2):
1. Выполняем присваивания  =1,
=1, 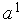 =
= 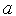 ,
, 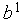 =
= 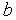 .
.
2. Вычисляем значения производных 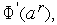
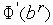 .
.
3. Если производные 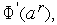
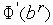 имеют одинаковые знаки – завершаем вычисления (точки
имеют одинаковые знаки – завершаем вычисления (точки 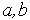 выбраны неверно).
выбраны неверно).
4. По формуле (5) вычисляем приближение 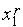 к стационарной точке функции
к стационарной точке функции  (
( ) и значение
) и значение 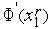 .
.
5. Если 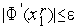 , где
, где 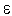 – требуемая точность решения, то принимаем
– требуемая точность решения, то принимаем 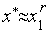 и заканчиваем вычисления.
и заканчиваем вычисления.
6. Если разные знаки имеют производные 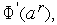
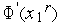 (как на рис. 2), то выполняем присваивания
(как на рис. 2), то выполняем присваивания 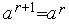 ,
, 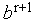 =
= 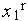 ,
, 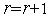 и переходим на п.4.
и переходим на п.4.
7. Если разные знаки имеют производные 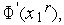
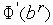 , то выполняем присваивания
, то выполняем присваивания 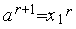 ,
, 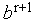 =
= 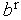 ,
, 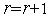 и переходим на п.4.
и переходим на п.4. 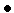
В случае квадратичной функции  (
( ) производная этой функции
) производная этой функции 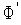 (
( ) линейна. Поэтому метод касательных гарантирует нахождение стационарной точки функции
) линейна. Поэтому метод касательных гарантирует нахождение стационарной точки функции  (
( ) всего за одну итерацию.
) всего за одну итерацию.
Также, как в методе хорд, возможна модификация метода касательных, когда значения производной 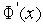 вычисляются приближенно с использованием первых разностей. В этом случае, очевидно, метод становится прямым (нулевого порядка).
вычисляются приближенно с использованием первых разностей. В этом случае, очевидно, метод становится прямым (нулевого порядка).
4.9 Повышение эффективности поиска на основе дополнительной информации о свойствах критерия оптимальности
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции  (
( ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 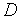 =[
=[ 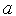 ,
, 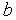 ],
],
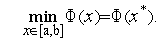 | (1) |
Всякая априорная информация о свойствах минимизируемой функции 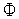 (
( ) может быть использована для повышения эффективности решения задачи (1).
) может быть использована для повышения эффективности решения задачи (1).
Положим, что имеется следующая априорная информация о минимизируемой функции: 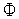 (
( ) является липшицевой функцией, т.е. принадлежит классу функций, которые на интервале [
) является липшицевой функцией, т.е. принадлежит классу функций, которые на интервале [ 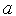 ,
, 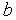 ] удовлетворяют условию Липшица с константой Липшица
] удовлетворяют условию Липшица с константой Липшица 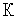
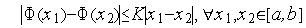
Покажем, как можно использовать данную априорную информация для сокращения текущего интервала неопределенности без проведения дополнительных испытаний.
Пусть после проведения  итераций каким-либо методом сокращения текущего интервала неопределенности имеет место ситуация:
итераций каким-либо методом сокращения текущего интервала неопределенности имеет место ситуация:
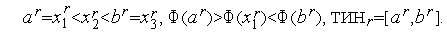
Обозначим 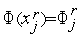 ,
, 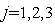 и проведем через точки (
и проведем через точки (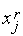 ,
, 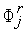 ),
), 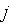 =1,3 прямые
=1,3 прямые 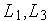 с тангенсами угла наклона к оси
с тангенсами угла наклона к оси 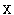 , равными
, равными 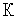 и (–
и (– 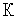 ), соответственно (см. рис. 1).
), соответственно (см. рис. 1).
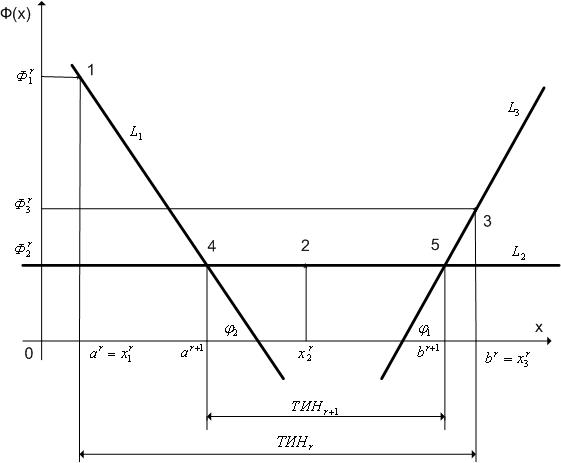 |
Рис. 1. Сужение интервала неопределенности за счет априорной информации о липшицевости минимизируемой функции. tg (φ1)= K, tg (φ2)=- K, φ2=180º-φ1.
Проведем, кроме того, через точку (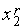 ,
, 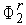 ) прямую
) прямую 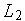 , параллельную оси
, параллельную оси 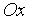 , до пересечения с прямыми
, до пересечения с прямыми 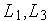 и обозначим абсциссы точек пересечения
и обозначим абсциссы точек пересечения 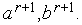
Утверждение 1. В сделанных предположениях, точки 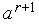 ,
, 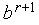 могут быть использованы в качестве границ интервала неопределенности
могут быть использованы в качестве границ интервала неопределенности 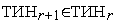 . Другими словами, в сделанных предположениях, точка
. Другими словами, в сделанных предположениях, точка 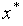 минимума функции
минимума функции 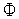 (
( ) не может лежать вне интервала
) не может лежать вне интервала 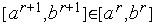
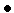
Найдем величины 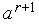 ,
, 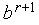 .
.
Прямая 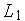 имеет уравнение
имеет уравнение 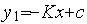 , где константа
, где константа 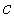 определяется из условия прохождения этой прямой через точку (
определяется из условия прохождения этой прямой через точку (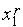 ,
, 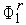 )
)
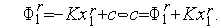
Таким образом, 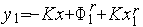 .
.
В точке (4) имеет место равенство 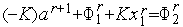 , из которого следует, что
, из которого следует, что
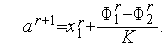
Аналогично для прямой 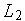
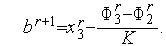
Глава 5. Методы поиска глобального минимума одномерных функций.
5.1 Метод перебора. Одномерный метод Монте-Карло
Некоторые методы решения многомерных задач оптимизации требуют решения одномерной задачи глобальной оптимизации (или совокупности таких задач).
Рассматривается следующая одномерная задача условной глобальной оптимизации): найти минимум, вообще говоря, многоэкстремальной функции  (
( ), определенной в замкнутой области допустимых значений
), определенной в замкнутой области допустимых значений 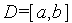 ,
,
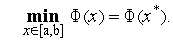 | (1) |
Метод перебора
Схема метода перебора (см. рис. 1):
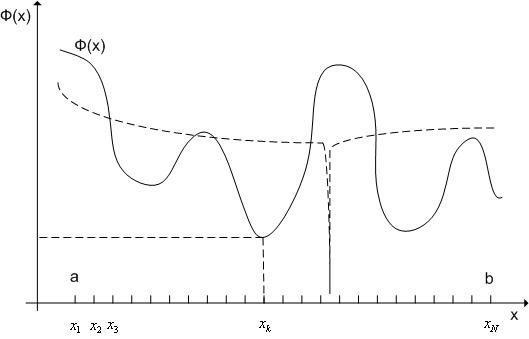 |
Рис. 1. К схеме метода перебора.
1. Покрываем интервал 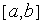 некоторой сеткой с узлами
некоторой сеткой с узлами 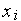 ,
, 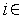 [1,
[1, 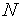 ].
].
2. Производим испытание в точке 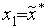 , т.е. вычисляем значения
, т.е. вычисляем значения 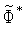 функции
функции 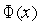 в этой точке.
в этой точке.
3. Полагаем 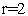 .
.
4. Производим испытание в точке 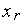 - вычисляем значение
- вычисляем значение 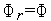 (
(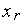 ) функции
) функции  (
( ) в этой точке.
) в этой точке.
5. Если 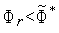 , то выполняем присваивания
, то выполняем присваивания 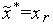 ,
, 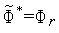 .
.
6. Если 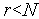 , то выполняем присваивание
, то выполняем присваивание 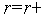 1 и переходим на п.4). Иначе - заканчиваем вычисления.
1 и переходим на п.4). Иначе - заканчиваем вычисления.
7. Принимаем 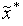 в качестве приближенного значения точки глобального минимума функции
в качестве приближенного значения точки глобального минимума функции  (
( ) на интервале [
) на интервале [ 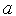 ,
, 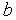 ] или каким-либо из рассмотренных одномерных методов локальной оптимизации организуем в окрестности точки
] или каким-либо из рассмотренных одномерных методов локальной оптимизации организуем в окрестности точки 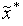 поиск локального минимума этой функции
поиск локального минимума этой функции
При выборе количества узлов сетки 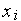 ,
, 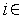 [1,
[1, 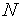 ] можно исходить из требуемой точности решения
] можно исходить из требуемой точности решения 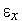 – максимальный шаг сетки принять равным этой величине.
– максимальный шаг сетки принять равным этой величине.
Отметим, что метод перебора, как и любой другой метод глобальной оптимизации, при отсутствии априорной информации о свойствах минимизируемой функции не гарантирует нахождение глобального минимума (см. пунктирный график на рис. 1).
Одномерный метод Монте-Карло
Схема одномерного метода Монте-Карло:
1. Генерируем с помощью какого-либо программного генератора случайных чисел, равномерно распределенных в интервале [ 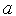 ,
, 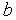 ], случайное число
], случайное число 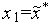 .
.
2. Производим испытание в точке 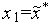 - вычисляем значения
- вычисляем значения 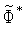 функции
функции  (
( ) в этой точке.
) в этой точке.
3. Полагаем 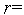 2.
2.
4. Аналогично п. 1) генерируем случайное число 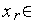 [
[ 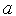 ,
, 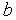 ].
].
5. Производим испытание в точке 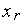 - вычисляем значение
- вычисляем значение 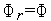 (
(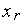 ) функции
) функции  (
( ) в этой точке.
) в этой точке.
6. Если
 2015-03-22
2015-03-22 886
886







