2015-03-22
2590
Симплексный метод или метод последовательного улучшения плана основан на идее перехода от одного базисного решения в вершине многоугольника допустимых решений к другому базисному решению, более близкому к оптимальному.
Задача ЛП формулируется следующим образом:
задана система ограничений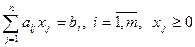 
.
Требуется найти максимум целевой функции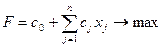 
.
Предполагается, что ранг системы равен числу уравнений m и меньше числа переменных n.
Пронумеруем переменные таким образом, чтобы вначале шли свободные переменные, а далее базисные переменные:
.
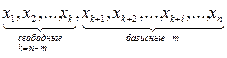Выразим базисные переменные и целевую функцию через свободные переменные:
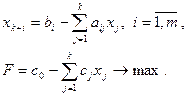
Для удобства использования алгоритма свободные переменные выделяем с отрицательными знаками:
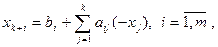(5.1)
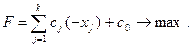(5.2)
Решение задачи осуществляется в симплексной таблице, у которой каждая строка соответствует уравнению из (5.1):
.
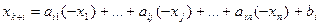Т. е. каждая строка симплекс-таблицы соответствует базисной переменной, а каждому столбцу соответствует свободная переменная xj и выделен столбец свободных членов (правых частей ограничений) bi. Внизу помещена строка целевой функции F.
Свободные переменные
| Базисные | -x1 … | -хj … | -xk | b | |
| xk+1 … | a11 | a1j | a1k | b1 … | |
| xk+ i … | ai1 | ajj | aik | bi … | |
| xn | am1 | amj | amk | bm | |
| F | c1 |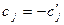 
| ck | c0 |
Решение системы, полученное приравниванием свободных переменных к нулю, называется базисным (опорным) решением.
Таким образом, в таблице записано следующее опорное решение:
xk+1=b, …, xk+i=bi , …, xn=bm, xj=0, j =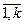 
.
При этом, как видно, целевая функция будет равна F=c0 .
Рассматриваются только те свободные переменные, которые входят в целевую функцию с отрицательным коэффициентом, например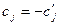 
. Увеличение такой переменной ведет к увеличению максимизируемой целевой функции. Если сохранить за остальными свободными переменными нулевое значение и начать увеличивать xj, то целевая функция будет увеличиваться, что и нужно для оптимизации.
Переменную xj можно увеличивать до тех пор, пока одна из базисных переменных xk+1,…,xn не обратится в ноль, например xk+i. Дальше увеличивать xj нельзя, т.к. переменная xk+i станет отрицательной, т.е. нарушится условие неотрицательности (xk+i ³ 0). А когда произойдет обращение в ноль базисной переменной можно установить из соотношений:
xk+1 = b1 - a1j xj,
…
xk+i = bi - aij xj, (5.3)
…
xn = bm - amj xj ;
F = c0 + cj xj .
Причем нас интересуют только те уравнения, в которых коэффициент aij>0, т.к. при aij£ 0 с увеличением xj соответствующая базисная переменная никогда не обратится в ноль.
Базисная переменная обратится в ноль, когда выполнится соотношение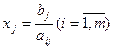 
.
Быстрее всех обратится в ноль та базисная переменная, для которой отношение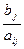 
является минимальным. Это отношение называется симплексным отношением. Остальные базисные переменные при этом будут еще положительны.
Коэффициент аij называется генеральным коэффициентом или разрешающим элементом.
Выведем переменную xj из числа свободных и сделаем ее базисной (т.к. раньше установили, что ее можно увеличить для оптимизации), а вместо нее введем переменную xk+i, которая быстрее других базисных переменных обратится в ноль. Теперь необходимо выразить целевую функцию F и новый набор базисных переменных (в который вошла xj) через набор новых свободных переменных, куда вошла xk+i. Допустим, надо поменять переменную xj на yi при разрешающем элементе aij в таблице 1 и получить новую таблицу 2.
Исходная таблица 1 Таблица 2
| -x1 | … | -xj | ® | -x1 | … | -yi | ||
| y1 | a11 | … | a1j | y1 | a11+ai1(-a1j/aij) | … | -a1j/aij | |
| … | … | … | … | … | … | … | … | |
| yi | a i1 | … | а ij | xj | ai1/aij | … | 1/aij |
Эти преобразования осуществляются в симплексной таблице по следующему алгоритму:
1. В таблице 1 выделяется разрешающий элемент на пересечении i -й строки и j -го столбца (aij).
2. В таблице 2 разрешающий элемент заменяется на обратную величину.
3. Все остальные элементы разрешающей строки i делятся на разрешающий элемент.
4. Все элементы разрешающего столбца j делятся на разрешающий элемент и меняют знак на противоположный.
5. Все остальные элементы, не принадлежащие разрешающим столбцу и строке, вычисляются по правилу «прямоугольника». Мысленно выделяется прямоугольник, в котором подлежащий пересчету элемент и разрешающий элемент образуют одну из диагоналей. Из произведения этих элементов вычитается произведение элементов, образующих другую диагональ прямоугольника, а результат делится на разрешающий элемент.
Сам алгоритм нахождения оптимального решения включает следующие операции.
1. Просматривается строка целевой функции F, и если среди ее коэффициентов, не считая свободного члена c0, все элементы положительны, то оптимальное решение достигнуто.
2. Если в строке F есть отрицательный коэффициент, а в столбце, соответствующем ему, нет ни одного положительного элемента, то целевая функция не ограничена и оптимального решения не существует.
3. Если в столбце над отрицательным коэффициентом целевой функции есть положительные элементы, то необходимо произвести замену соответствующей свободной переменной на базисную. В качестве разрешающего берется тот элемент выбранного столбца, который имеет одинаковый знак со свободным членом, и для которого симплексное соотношение минимально. С этим разрешающим элементом осуществляется шаг преобразования таблицы.
4. Операции 1, 2, 3 повторяются до получения оптимального решения.
