В линейной множественной регрессии 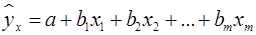 параметры при
параметры при 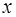 называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
Рассмотрим линейную модель множественной регрессии
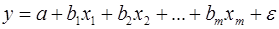 . (1)
. (1)
МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака 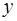 от расчетных
от расчетных 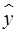 минимальна:
минимальна:
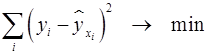 . (2)
. (2)
Вычислим частные производные первого порядка по каждому из параметров и приравняем их к нулю.
Имеем функцию 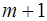 аргумента:
аргумента:
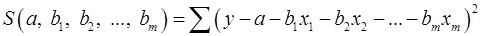 .
.
Находим частные производные первого порядка:
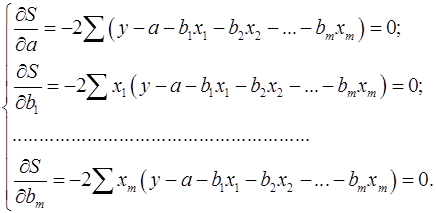
После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии (1):
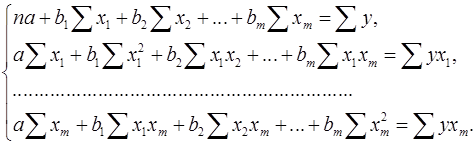 (3)
(3)
Для двухфакторной модели данная система будет иметь вид:
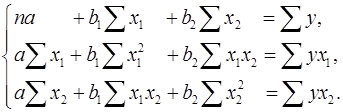
Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:
|
|
|
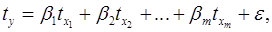 (4)
(4)
где 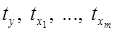 – стандартизированные переменные:
– стандартизированные переменные:
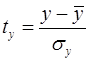 ,
, 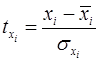 , для которых среднее значение равно нулю:
, для которых среднее значение равно нулю: 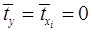 , а среднее квадратическое отклонение равно единице:
, а среднее квадратическое отклонение равно единице: 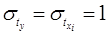 ;
;
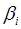 – стандартизированные коэффициенты регрессии.
– стандартизированные коэффициенты регрессии.
Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида
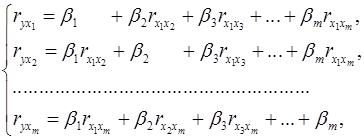 (5)
(5)
где 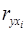 и
и 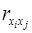 – коэффициенты парной и межфакторной корреляции.
– коэффициенты парной и межфакторной корреляции.
Коэффициенты «чистой» регрессии 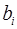 связаны со стандартизованными коэффициентами регрессии
связаны со стандартизованными коэффициентами регрессии 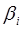 следующим образом:
следующим образом:
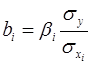 . (6)
. (6)
Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (4) к уравнению регрессии в натуральном масштабе переменных (1), при этом параметр 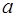 определяется как
определяется как 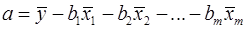 .
.
На основе линейного уравнения множественной регрессии
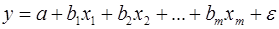 (7)
(7)
могут быть найдены частные уравнения регрессии:
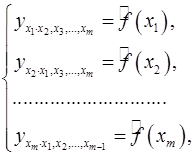 (8)
(8)
т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором 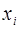 при закреплении остальных факторов на среднем уровне.
при закреплении остальных факторов на среднем уровне.
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем
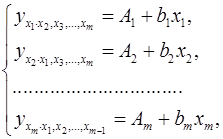 (9)
(9)
где
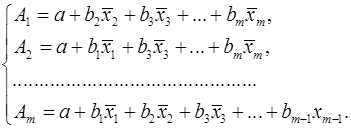
На основе частных уравнений регрессии определяются частные коэффициенты эластичности:
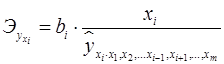 , (10)
, (10)
где 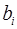 – коэффициент регрессии для фактора
– коэффициент регрессии для фактора 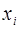 в уравнении множественной регрессии,
в уравнении множественной регрессии,
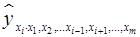 – частное уравнение регрессии.
– частное уравнение регрессии.
Наряду с частными коэффициентами эластичности могут быть найдены средние по совокупности показатели эластичности:
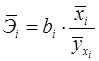 , (11)
, (11)
которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.
|
|
|
Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:
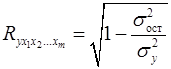 , (12)
, (12)
где 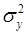 – общая дисперсия результативного признака;
– общая дисперсия результативного признака; 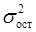 – остаточная дисперсия.
– остаточная дисперсия.
Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:
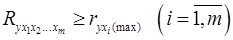 .
.
Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:
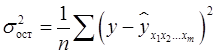 . (13)
. (13)
Можно пользоваться следующей формулой индекса множественной детерминации:
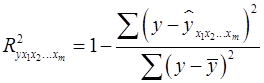 . (14)
. (14)
При линейной зависимости признаков формула индекса множественной корреляции может быть представлена следующим выражением:
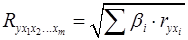 , (15)
, (15)
где 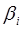 – стандартизованные коэффициенты регрессии;
– стандартизованные коэффициенты регрессии;
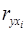 – парные коэффициенты корреляции результата с каждым фактором.
– парные коэффициенты корреляции результата с каждым фактором.
при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:
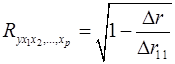 , (2.16)
, (2.16)
где
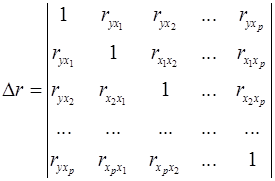 – определитель матрицы парных коэффициентов корреляции;
– определитель матрицы парных коэффициентов корреляции;
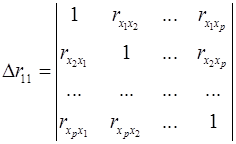 – определитель матрицы межфакторной корреляции.
– определитель матрицы межфакторной корреляции.
Как видим, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.
В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений 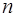 . Если число параметров при
. Если число параметров при 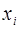 равно
равно 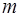 и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.
и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.
Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов 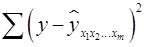 делится на число степеней свободы остаточной вариации
делится на число степеней свободы остаточной вариации 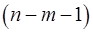 , а общая сумма квадратов отклонений
, а общая сумма квадратов отклонений 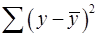 на число степеней свободы в целом по совокупности
на число степеней свободы в целом по совокупности 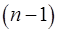 .
.
Формула скорректированного индекса множественной детерминации имеет вид:
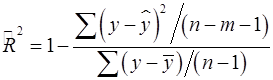 , (17)
, (17)
где 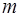 – число параметров при переменных
– число параметров при переменных 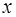 ;
;
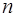 – число наблюдений.
– число наблюдений.
Поскольку 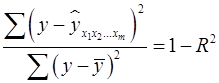 , то величину скорректированного индекса детерминации можно представить в виде:
, то величину скорректированного индекса детерминации можно представить в виде:
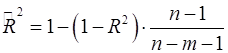 . (17а)
. (17а)
Чем больше величина 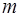 , тем сильнее различия
, тем сильнее различия 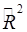 и
и 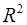 .
.
Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
В общем виде при наличии 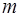 факторов для уравнения
факторов для уравнения
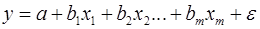
коэффициент частной корреляции, измеряющий влияние на 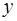 фактора
фактора 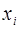 , при неизменном уровне других факторов, можно определить по формуле:
, при неизменном уровне других факторов, можно определить по формуле:
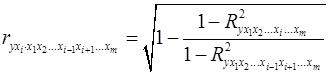 , (18)
, (18)
где 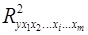 – множественный коэффициент детерминации всех
– множественный коэффициент детерминации всех 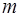 факторов с результатом;
факторов с результатом;
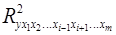 – тот же показатель детерминации, но без введения в модель фактора
– тот же показатель детерминации, но без введения в модель фактора 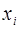 .
.
|
|
|
При двух факторах формула (2.18) примет вид:
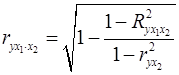 ;
; 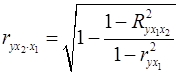 . (18а)
. (18а)
Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:
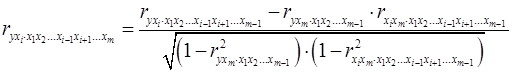 (19)
(19)
При двух факторах данная формула примет вид:
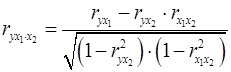 ;
; 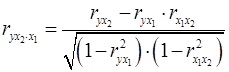 . (19а)
. (19а)
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по уравнению 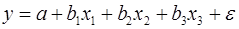 возможно исчисление трех частных коэффициентов корреляции второго порядка:
возможно исчисление трех частных коэффициентов корреляции второго порядка:
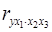 ,
, 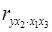 ,
, 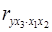 ,
,
каждый из которых определяется по рекуррентной формуле. Например, при 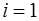 имеем формулу для расчета
имеем формулу для расчета 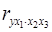 :
:
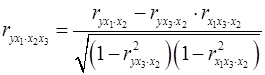 . (20)
. (20)
Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1
Совокупный коэффициент корреляции по формуле:
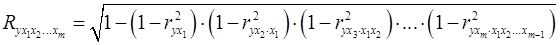 . (21)
. (21)
В частности, для двухфакторного уравнения формула (21) принимает вид:
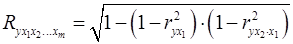 . (21)
. (21)
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью 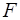 -критерия Фишера:
-критерия Фишера:
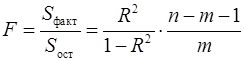 , (22)
, (22)
где 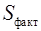 – факторная сумма квадратов на одну степень свободы;
– факторная сумма квадратов на одну степень свободы;
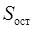 – остаточная сумма квадратов на одну степень свободы;
– остаточная сумма квадратов на одну степень свободы;
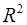 – коэффициент (индекс) множественной детерминации;
– коэффициент (индекс) множественной детерминации;
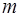 – число параметров при переменных
– число параметров при переменных 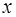 (в линейной регрессии совпадает с числом включенных в модель факторов);
(в линейной регрессии совпадает с числом включенных в модель факторов);
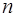 – число наблюдений.
– число наблюдений.
Частный 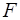 -критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. В общем виде для фактора
-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. В общем виде для фактора 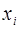 частный
частный 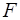 -критерий определится как
-критерий определится как
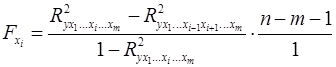 , (23)
, (23)
где 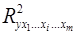 – коэффициент множественной детерминации для модели с полным набором факторов,
– коэффициент множественной детерминации для модели с полным набором факторов,
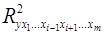 – тот же показатель, но без включения в модель фактора
– тот же показатель, но без включения в модель фактора 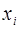 ,
,
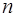 – число наблюдений,
– число наблюдений,
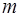 – число параметров в модели (без свободного члена).
– число параметров в модели (без свободного члена).
Фактическое значение частного 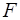 -критерия сравнивается с табличным при уровне значимости
-критерия сравнивается с табличным при уровне значимости 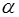 и числе степеней свободы: 1 и
и числе степеней свободы: 1 и 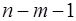 . Если фактическое значение
. Если фактическое значение 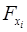 превышает
превышает 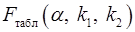 , то дополнительное включение фактора
, то дополнительное включение фактора 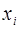 в модель статистически оправданно и коэффициент чистой регрессии
в модель статистически оправданно и коэффициент чистой регрессии 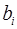 при факторе
при факторе 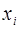 статистически значим. Если же фактическое значение
статистически значим. Если же фактическое значение 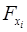 меньше табличного, то дополнительное включение в модель фактора
меньше табличного, то дополнительное включение в модель фактора 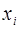 не увеличивает существенно долю объясненной вариации признака
не увеличивает существенно долю объясненной вариации признака 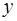 , следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.
, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.
|
|
|
Для двухфакторного уравнения частные 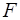 -критерии имеют вид:
-критерии имеют вид:
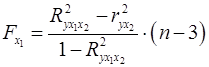 ,
, 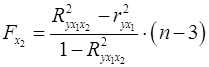 . (23а)
. (23а)
С помощью частного 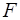 -критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор
-критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор 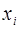 вводился в уравнение множественной регрессии последним.
вводился в уравнение множественной регрессии последним.
Частный 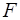 -критерий оценивает значимость коэффициентов чистой регрессии. Зная величину
-критерий оценивает значимость коэффициентов чистой регрессии. Зная величину 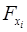 , можно определить и
, можно определить и 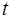 -критерий для коэффициента регрессии при
-критерий для коэффициента регрессии при 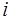 -м факторе,
-м факторе, 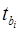 , а именно:
, а именно:
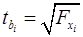 . (24)
. (24)
Оценка значимости коэффициентов чистой регрессии по 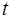 -критерию Стьюдента может быть проведена и без расчета частных
-критерию Стьюдента может быть проведена и без расчета частных 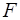 -критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула:
-критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула:
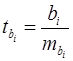 , (25)
, (25)
где 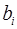 – коэффициент чистой регрессии при факторе
– коэффициент чистой регрессии при факторе 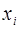 ,
,
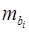 – средняя квадратическая (стандартная) ошибка коэффициента регрессии
– средняя квадратическая (стандартная) ошибка коэффициента регрессии 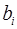 .
.
Для уравнения множественной регрессии 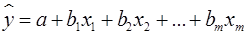 средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:
средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:
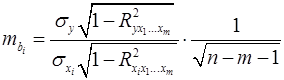 , (26)
, (26)
где 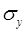 – среднее квадратическое отклонение для признака
– среднее квадратическое отклонение для признака 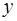 ,
,
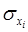 – среднее квадратическое отклонение для признака
– среднее квадратическое отклонение для признака 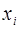 ,
,
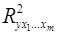 – коэффициент детерминации для уравнения множественной регрессии,
– коэффициент детерминации для уравнения множественной регрессии,
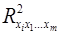 – коэффициент детерминации для зависимости фактора
– коэффициент детерминации для зависимости фактора 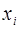 со всеми другими факторами уравнения множественной регрессии;
со всеми другими факторами уравнения множественной регрессии;
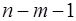 – число степеней свободы для остаточной суммы квадратов отклонений.
– число степеней свободы для остаточной суммы квадратов отклонений.
Как видим, чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет по ней соответствующих коэффициентов детерминации 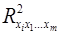 . Так, для уравнения
. Так, для уравнения 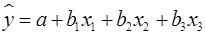 оценка значимости коэффициентов регрессии
оценка значимости коэффициентов регрессии 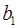 ,
, 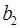 ,
, 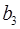 предполагает расчет трех межфакторных коэффициентов детерминации:
предполагает расчет трех межфакторных коэффициентов детерминации: 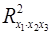 ,
, 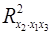 ,
, 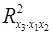 .
.
 2015-03-27
2015-03-27 3001
3001







