Сопряженные гармонические функции

Действительная функция U(x,y), имеющая в области D непрерывные частные производные второго порядка и удовлетворяющая уравнению

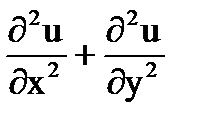=0 (25.21)

или 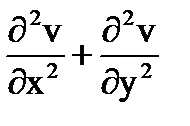=0

называется гармонической в области D, а уравнение (25.21) - уравнением Лапласа.

Гармонические функции U(x,y), V(x,y), связанные между собой условиями Коши-Римана:

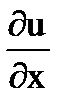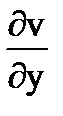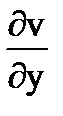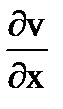= , =- (25.22)

называются сопряженными.

Таким образом, действительная и мнимая части дифференцируемых в области D функций являются в этой области сопряженными гармоническими функциями.

Теорема 25.2. Для дифференцируемости функции f(x)=u+iv в области D необходимо и достаточно, чтобы функции U(x,y)V(x,y) были сопряженными гармоническими в этой области (Доказательство смотрите [2 стр.63]).

Теорема25.3. Для всякой функции L(x,y) гармонической в односвязной области D, можно найти сопряженную с ней гармоническую функцию, которая определяется с точностью до произвольного постоянного слагаемого (Доказательство смотрите[ [7].стр.63]).