Частотные характеристики

Пусть на вход устойчивой системы или звена подается гармонический сигнал вида

f(t) = af× sinwt. (3.10)

Учитывая, что

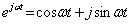, (3.11)

целесообразно найти вынужденную реакцию системы на воздействие вида 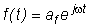, (3.12)

а затем учесть мнимую часть этой вынужденной реакции (см. формулы (3.10) и (3.11)).

Линейная система описывается передаточной функцией

,

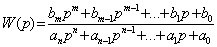т.е. описывается дифференциальным уравнением

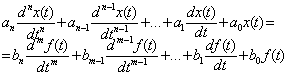
При входном сигнале (3.12) сигнал на выходе найдем в виде

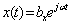. (3.13)

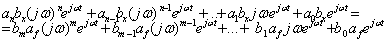(3.14)

Отношение комплексных амплитуд выходного сигнала (после затухания свободного движения) и входного гармонического сигнала

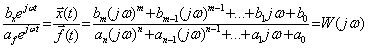, (3.15)

называют частотной передаточной функцией (ЧПФ), или комплексным коэффициентом передачи (ККП).

На основании формулы (3.15) можно записать

bx = afW(jw). (3.16)

Используя соотношения (3.10) и (3.11), можно записать

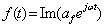. (3.17)

Тогда

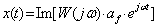. (3.18)

Выделяя в выражении (3.15) действительную и мнимую части, можно записать

W(jw) = Re W(jw) + jIm W(jw) = U(w) + jV(w) = A(w) 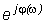, (3.19)

где

A(w) = 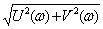- модуль ЧПФ, (3.20)

j(w) = arctg(V(w)/U(w)) - аргумент ЧПФ. (3.21)

Выражение (3.18) с учетом (3.19) можно записать в следующем виде

x(t)=Im[A(w)af 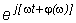]= A(w)af × sin[wt+j(w)]=ax × sin[wt+j(w)]. (3.22)

Следовательно, при подаче на вход устойчивой линейной системы гармонического сигнала на ее выходе после затухания свободного движения установится гармонический сигнал с той же частотой, но амплитудой

ax = A(w)af (3.23)

и со сдвигом по фазе

j(w) = arg W(jw).

Соотношения (3.22) и (3.23) позволяют установить физический смысл модуля и аргумента ЧПФ.

Модуль ЧПФ есть отношение амплитуд выходного и входного сигналов системы в режиме установившихся гармонических колебаний на данной частоте.

Аргумент ЧПФ - сдвиг по фазе между выходным и входным сигналами системы в режиме установившихся гармонических колебаний на данной частоте.

Графики функций A(w) и j(w) называются соответственно амплитудной частотной (АЧХ) и фазовой частотной (ФЧХ) характеристиками.

Указанный выше физический смысл каждой ординаты A(w) и j(w) является основанием для экспериментального получения АЧХ и ФЧХ линейных звеньев и систем.

Графики АЧХ и ФЧХ, построенные в логарифмическом масштабе, называют логарифмическими частотными характеристиками: ЛАЧХ и ЛФЧХ. Зачем нужны логарифмические частотные характеристики (ЛЧХ)? Для ответа на этот вопрос рассмотрим частотные характеристики последовательного соединения звеньев.

При последовательном соединении звеньев (см. (2.44))

W(p)= .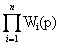

Заменяя p на jw, можно записать

W(jw)= . (3.24)

Учитывая, что W(jw)= A(w) 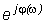(3.25)

Wi (jw)= Ai (w) 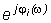(3.26)

и подставляя выражения (3.25) и (3.26) в формулу (3.24), получим

A(w) = ,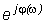

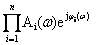откуда следует, что

A(w)= 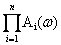; (3.27)

j(w) = 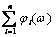. (3.28)

Выражения (3.27) и (3.28) показывают, что для вычисления частотных характеристик последовательного соединения звеньев необходимо для каждого из фиксированных значений частот перемножить модули ЧПФ и суммировать их аргументы. Для того, чтобы исключить операции умножения целесообразно использовать логарифмические характеристики. Из (3.27) следует:

L(w) = 20lgA(w) = ;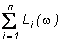

Li(w) = 20lgAi(w).

Для их построения по оси абсцисс откладываются значения частот в логарифмическом масштабе. Эта ось равномерно разбивается на декады. Декада соответствует десятикратному изменению частоты (в рад/с), например, от 0,1 до 1, от 1 до 10 и т.д. Масштабирование каждой декады выполняется одинаково на основе следующего соотношения

mw = mдек × (мантисса десятичного логарифма цифр от 2 до 9),

где mдек - масштаб декады в мм,

mw - масштаб частоты от начала своей декады (своего порядка).

При построении ЛАЧХ значение модуля ЧПФ откладывается в децибелах (дБ) в равномерном масштабе. Если модуль ЧПФ A(w), то число децибел равно L(w)=20lgA(w) дБ.

При построении ЛФЧХ по оси ординат откладывается значение j(w) в градусах или радианах.

В заключение отметим, что за редким исключением строят не точные, а асимптотические ЛАЧХ (см. пример 3.1).