Частной производной 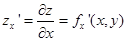 от функции двух переменных f (x, y) по переменной х при y = y 0 называется предел, при Δ х стремящемся к нулю, отношения частного по х приращения функци
от функции двух переменных f (x, y) по переменной х при y = y 0 называется предел, при Δ х стремящемся к нулю, отношения частного по х приращения функци 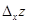 к вызвавшему его приращению аргумента Δ х (если этот предел существует и конечен). Так как y0 любое фиксированное число из области допустимых значений, то его можно заменить на просто у. Тогда
к вызвавшему его приращению аргумента Δ х (если этот предел существует и конечен). Так как y0 любое фиксированное число из области допустимых значений, то его можно заменить на просто у. Тогда
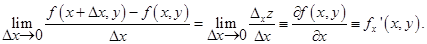
Частная производная от функции f (x, y) по переменной y 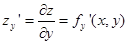 определяется и обозначается аналогичным образом
определяется и обозначается аналогичным образом
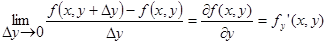
То есть, при вычислении частной производной от функции двух переменных f (x, y) по х второй аргумент y выступает как величина постоянная. Если же вычисляется частная производная по y, то х принимается постоянной величиной.
Пример 1. Вычислить частные производные zx¢ и zy¢ от функции
f (x, y) = x 3 y 2 + sin x - 4 y.
Решение. В соответствии с определением, имеем
f x¢(x, y) = 3 x 2 y 2 + cos x и f y¢(x, y) = 2 x 3 y - 4.
Частная производная от f (x, y) тоже является функцией двух переменных и от нее вновь можно вычислять частные производные и так далее.
|
|
|
Функция двух переменных имеет следующие вторые производные:
- вторая производная от f (x, y) по х дважды
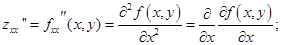
- вторая производная от f (x, y) по y дважды
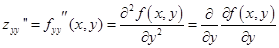
- вторая смешанная производная от f (x, y) по x и по y
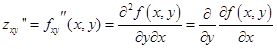
- вторая смешанная производная от f (x, y) по y и по х.
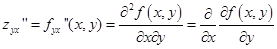
для функций, имеющих непрерывные частные производные второго порядка, смешанные производные второго порядка совпадают
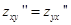
Пример 2 ( продолжение примера 1). Вычислить вторые производные для функции
f (x, y) = x 3 y 2 + sin x - 4 y.
Решение. Применяя правила дифференцирования, получим
z xx¢¢ = (3 x 2 y 2 + cos x)х’ = 6 xy 2 - sin x,
zyy ¢¢ = (2 x 3 y – 4)y’ = 2 x 3,
zxy ¢¢ = (3 x 2 y 2 + cos x)y’ = 6 x 2 y = zyx ¢¢.
Теперь не представляет труда решение задачи о вычислении производных любого порядка.
Пример 3. Вычислить четвертую производную, причем одну по х и три по y для функции
f (x, y) = 2 x 4 ּ ln y - cos(x + y 3) + x 3
В соответствии и правилами дифференцирования сложных функций и функций многих переменных имеем:
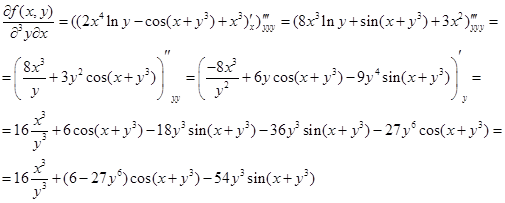
Производные от функций большего числа производных вычисляются по тем же правилам.
Пример 4. Пусть дана функция четырех переменных f(x,y,z,t)
f(x, y, z, t) = xz 3 t 2 + yz 2 cos(y 3 - t).
Решение. Вычислим вторую смешанную производную по аргументам z и t
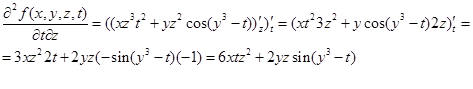
 2015-03-07
2015-03-07 3090
3090
