Рассмотрим простейший случай, когда плановые ремонты или любые другие преднамеренные отключения отсутствуют. Элемент СЭС находится в эксплуатации до тех пор, пока не откажет. После отказа выполняется его аварийный ремонт, и элемент снова поступает в эксплуатацию.
Такая упрощенная математическая модель не является чистой абстракцией и соответствует стратегии обслуживания с аварийными ремонтами. По стратегии аварийных ремонтов эксплуатируется практически вся бытовая техника, ряд мало ответственных промышленных потребителей, сельского хозяйства и других отраслей народного хозяйства. Более того, при низком значении ущерба от отказа стратегия аварийных ремонтов является оптимальной с точки зрения минимума средних удельных затрат на ремонт и восстановление [2]. Даже при наличии профилактического обслуживания, его в ряде случаев можно не учитывать. На промышленных предприятиях профилактические ремонты элементов СЭС часто выполняются в выходные или праздничные дни, совместно с ремонтом технологического оборудования, не оказывают влияния на производственный процесс и не ведут к ущербам.
|
|
|
Элемент СЭС без преднамеренных отключений будет иметь лишь два состояния: 0 – работоспособное; 1 – состояние аварийного восстановления. Цепь Маркова для такого элемента может быть изображена в виде направленного графа (рис.2.2), у которого вершины изображают соответствующие состояния элемента, а ребра – события переходов, отказов или восстановлений.
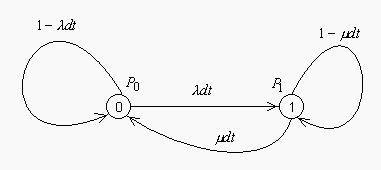
Рис.2.2. Цепь Маркова для элемента без преднамеренных отключений
Пусть в момент времени 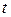 элемент находится в работоспособном состоянии с вероятностью
элемент находится в работоспособном состоянии с вероятностью 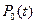 . Условная вероятность того, что за время
. Условная вероятность того, что за время 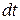 не произойдет отказа и элемент останется в работоспособном состоянии равна
не произойдет отказа и элемент останется в работоспособном состоянии равна
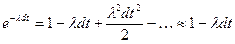 . .
|
Безусловная вероятность того, что на интервале времени 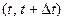 отказа не произойдет, равна произведению
отказа не произойдет, равна произведению 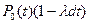 . С другой стороны в момент времени
. С другой стороны в момент времени 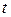 с вероятностью
с вероятностью 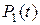 элемент мог находиться в состоянии аварийного ремонта. За время
элемент мог находиться в состоянии аварийного ремонта. За время 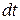 ремонт может завершиться с вероятностью
ремонт может завершиться с вероятностью 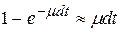 . А вероятность перехода элемента из состояния 1 в состояние 0 равна произведению
. А вероятность перехода элемента из состояния 1 в состояние 0 равна произведению 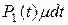 .
.
Таким образом, к моменту времени 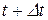 элемент либо останется в состоянии 0, либо перейдет из состояния 1 в состояние 0, а вероятность
элемент либо останется в состоянии 0, либо перейдет из состояния 1 в состояние 0, а вероятность 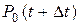 будет равна сумме
будет равна сумме
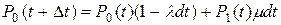 .
.
Раскрывая скобки, получим дифференциальное уравнение относительно вероятности пребывания элемента в работоспособном состоянии:
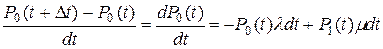 . .
| (2.12) |
Аналогично для состояния аварийного ремонта получим:
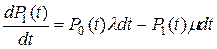 . .
| (2.13) |
Уравнения (2.12), (2.13) представляют собой систему дифференциальных уравнений относительно вероятностей 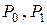 . Их решение зависит от начальных условий.
. Их решение зависит от начальных условий.
|
|
|
Естественно принять, что в начале срока эксплуатации элемент полностью работоспособен, то есть 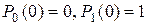 . Для указанных начальных условий решение системы уравнений (2.12), (2.13) может быть записано в виде:
. Для указанных начальных условий решение системы уравнений (2.12), (2.13) может быть записано в виде:
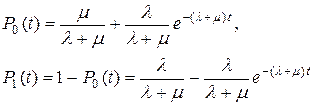 . .
| (2.14) |
Вероятность застать элемент в работоспособном состоянии определяет его коэффициент готовности 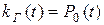 . Коэффициент аварийного простоя, как вероятность застать элемент в произвольный момент времени
. Коэффициент аварийного простоя, как вероятность застать элемент в произвольный момент времени 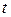 в неработоспособном состоянии, равен
в неработоспособном состоянии, равен 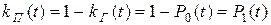 .
.
 2015-03-20
2015-03-20 585
585








