Основную роль во всей арифметике целых чисел играет теорема о делении с остатком.
Теорема 4.1. Для любого целого а и целого 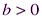 существуют и единственные целые q и r, такие что
существуют и единственные целые q и r, такие что 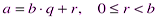 .
.
Замечание 4.3. Если 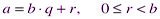 то q называется неполным частным, а r – остатком от деления a на b.
то q называется неполным частным, а r – остатком от деления a на b.
Замечание 4.2. В частности, если 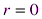 , то
, то 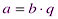 и
и 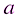 делится на
делится на 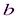 .
.
Из теоремы 4.1 следует, что при фиксированном целом m > 0 любое целое число а можно представить в одном из следующих видов:
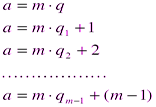
При этом если 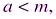 то будем иметь
то будем иметь 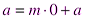 , если
, если 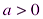 и
и
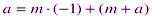 , если
, если 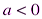 .
.
Примеры.
1.
Любое целое число можно представить в виде 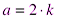 или
или 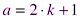 .
.
2.
Любое целое число можно представить в виде 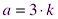 или
или 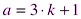 или
или 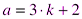 .
.
Важным следствием из теоремы о делении с остатком является еще одно свойство делимости.
Теорема 4.4. Разность целых чисел а и b делится на натуральное число m в том и только в том случае, когда числа а и b при делении на m дают одинаковые остатки.
Замечание. Такие числа называют еще равноостаточными, или сравнимыми по модулю m.
На следующей теореме основан ещё один способ нахождения наибольшего общего делителя целых чисел.
|
|
|
Теорема 4.5. Пусть a и b – два целых числа, 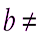 0и
0и  ,
, 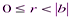 тогда
тогда 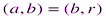 .
.
Этот способ называется алгоритмом Евклида. Задача нахождения НОД чисел a и b сводится к более простой задаченахождения НОД b и r, 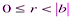 . Если r = 0, то
. Если r = 0, то 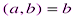 . Если же
. Если же 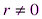 , то рассуждения повторяем, отправляясь от b и r. В результате получаем цепочку равенств:
, то рассуждения повторяем, отправляясь от b и r. В результате получаем цепочку равенств:
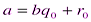 ,
, 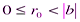 ,
,
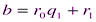 ,
, 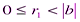 ,
,
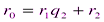 ,
, 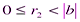 , ……………………(**)
, ……………………(**)
………….. ………..
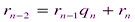 ,
, 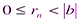 ,
,
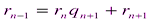 .
.
Мы получим убывающую последовательность натуральных чисел
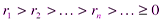
которая не может быть бесконечной. Поэтому существует остаток, равный нулю: пусть 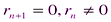 . На основании теоремы 4.5 из (**) следует, что
. На основании теоремы 4.5 из (**) следует, что 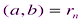 .
.
 2015-04-12
2015-04-12 6386
6386
