Плоскость. Теорема. В декартовой системе координат каждая плоскость определяется уравнением первой степени

Теорема. В декартовой системе координат каждая плоскость определяется уравнением первой степени. И обратно: в декартовой системе координат каждое уравнение первой степени определяет плоскость.

Доказательство. Пусть существует произвольная плоскость 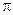. Пусть точка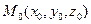 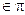. Пусть задан вектор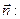 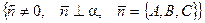. Пусть 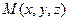– произвольная точка пространства с переменными координатами. Условие принадлежности точки М плоскости 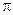– это перпендикулярность векторов 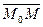и :

.

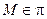
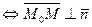Выразим условие принадлежности т. 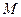к плоскости 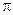через координаты векторов 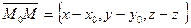и .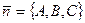

Условие перпендикулярности векторов:

(*)

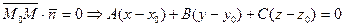– это и есть уравнение плоскости 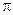, поскольку ему удовлетворяют только точки плоскости. Преобразуем его:

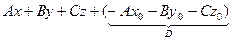= 0 или

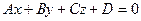. (1)

Уравнение (1) – это общее уравнение плоскости. Таким образом, плоскость 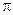действительно определяется уравнением первой степени.

Докажем второе утверждение. Пусть дано произвольное уравнение первой степени (1): .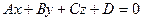

Пусть 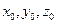- решение данного уравнения.

Тогда равенство 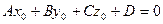– тождество. (2)

Вычтем тождество (2) из уравнения (1), получим

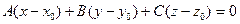. (3)

Это уравнение плоскости, проходящей через заданную точку 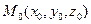и имеющей нормаль 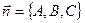(см. уравнение (*)).

Уравнение (1) равносильно уравнению (3), т. к. они получаются друг из друга путем почленного вычитания тождества. Следовательно, уравнение (1) является уравнением той же плоскости. Теорема доказана.

Рассмотрим два общих уравнения плоскостей. Пусть они определяют одну и ту же плоскость 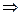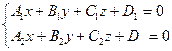(4)

Тогда нормали и 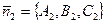коллинеарны, а, следовательно, коэффициенты уравнений пропорциональны: .

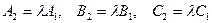Умножим первое уравнение системы на 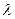и вычтем его из второго уравнения. Получим: .

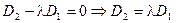Вывод. Если два уравнения определяют одну и ту же плоскость, то их коэффициенты пропорциональны.