Пример 1. Вычислить для атома водорода радиус первой боровской орбиты и скорости электрона на ней.
Решение. Радиус n–й боровской орбиты rn и скорость un электрона на ней связаны между собой уравнением первого постулата Бора:
munrn = ћn. (3.1)
Чтобы иметь еще одно уравнение, связывающие величины un и rn, запишем второй закон Ньютона для электрона, движущегося под действием кулоновской силы притяжения ядра по круговой орбите. Учитывая, что ядром атома водорода является протон, заряд которого равен по модулю заряду электрона, запишем:
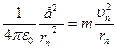 , (3.2)
, (3.2)
где m – масса электрона, 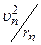 – нормальное ускорение. Решив совместно (3.1) и (3.2) получим:
– нормальное ускорение. Решив совместно (3.1) и (3.2) получим:
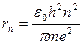 ,
, 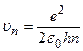 .
.
Положив здесь n = 1, произведем вычисления:
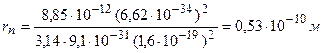 ;
; 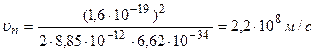 .
.
Пример 2. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Определить энергию испущенного при этом фотона и его длину волны.
Решение. Для определения энергии фотона воспользуемся сериальной формулой для водородоподобных ионов:
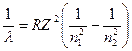 , (3.3)
, (3.3)
где λ – длина волны фотона; R – постоянная Ридберга; Z – заряд ядра в относительных единицах (при Z = 1 формула переходит в сериальную формулу для водорода); n1 – номер орбиты, на которую перешел электрон; n2 – номер орбиты, с которой перешел электрон (n1 и n2 – главные квантовые числа).
|
|
|
Энергия фотона Е выражается формулой
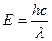 . (3.4)
. (3.4)
Поэтому, умножив обе части равенства (13.3) на hc, получим выражение для энергии фотона:
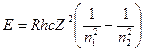 .
.
Т.к. Rhc есть энергия ионизации Ei атома водорода, то
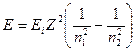 .
.
Из равенства (3.4) выразим длину волны фотона
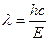
Вычисления выполним во внесистемных единицах: Ei = 13,6 эВ; Z = 1; n1 = 2; n2 = 4:
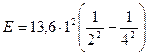 эВ = 2,55 эВ.
эВ = 2,55 эВ.
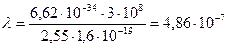 м.
м.
Пример 3. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля электрона для двух случаев: 1) U1 = 51 В; 2) U2 = 510 кВ.
Решение. Длина волны де Бройля для частицы зависит от ее импульса р и определяется формулой
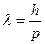 , (3.5)
, (3.5)
где h – постоянная Планка.
Импульс частицы можно определить, если известна ее кинетическая энергия Т. Связь импульса с кинетической энергией различна для нерелятивистского случая (когда кинетическая энергия частицы много меньше ее энергии покоя) и для релятивистского случая (когда кинетическая энергия сравнима с энергией покоя частицы).
В нерелятивистском случае
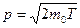 , (3.6)
, (3.6)
где m0 – масса покоя частицы.
В релятивистском случае
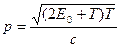 , (3.7)
, (3.7)
где E0 = m0с2 – энергия покоя частицы.
Формула (3.5) с учетом соотношений (3.6) и (3.7) запишется:
- в нерелятивистском случае
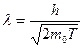 , (3.8)
, (3.8)
- в релятивистском случае
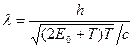 . (3.9)
. (3.9)
Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U1 = 51 В и U2 = 510 кВ, с энергией покоя электрона и в зависимости от этого решим, какую из формул (3.8) или (3.9) следует применить для вычисления длины волны де Бройля.
|
|
|
Как известно, кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U,
T = eU.
В первом случае T1 = еU1 = 51 эВ= 0,51 10-4 МэВ, что много меньше энергии покоя электрона Е0 = m0с2 = 0,51 МэВ. Следовательно, в этом случае можно применить формулу (3.8). Для упрощения расчетов заметим, что T1 = 10-4 m0c2. Подставив это выражение в формулу (3.8), перепишем ее в виде
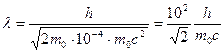 .
.
Учитывая, что 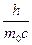 есть комптоновская длина волны λ, получаем
есть комптоновская длина волны λ, получаем
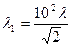 .
.
Т.к. λ = 2,43пм, то
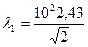 = 171 пм.
= 171 пм.
Во втором случае кинетическая энергия T2 = eU2 = 510 кэВ = 0,51 МэВ, т.е. равна энергии покоя электрона. В этом случае необходимо применить релятивистскую формулу (3.9). Учитывая, что Т2 = 0,51МэВ = m0с2, по формуле (3.9) находим
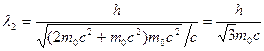 ,
,
или
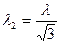 .
.
Подставим значение λи произведем вычисления:
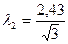 = 1,40 пм.
= 1,40 пм.
Пример 4. Кинетическая энергия электрона в атоме водорода составляет величину порядка Т = 10 эВ. Используя соотношение неопределенностей, оценить минимальные линейные размеры атома.
Решение. Соотношение неопределенностей для координаты и импульса имеет вид
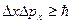 , (3.10)
, (3.10)
где Dх – неопределенность координаты частицы (в данном случае электрона); Dрх – неопределенность импульса частицы (электрона); 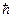 – постоянная Планка.
– постоянная Планка.
Из соотношения неопределенностей следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а, следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью
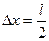 .
.
Соотношение неопределенностей (3.10) можно записать в этом случае в виде
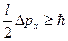 ,
,
откуда
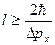 . (3.11)
. (3.11)
Физически разумная неопределенность импульса Dрх во всяком случае не должна превышать значения самого импульса рх, т.е. Dрх £ рх. Импульс рх связан с кинетической энергией Т соотношением
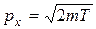 . Заменим Dрх значением
. Заменим Dрх значением 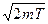 (такая замена не увеличит l). Переходя от неравенства к равенству, получим
(такая замена не увеличит l). Переходя от неравенства к равенству, получим
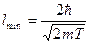 . (3.12)
. (3.12)
Проверим, дает ли полученная формула единицу длины. Для этого в правую часть формулы (3.12) вместо символов величин подставим обозначения их единиц:
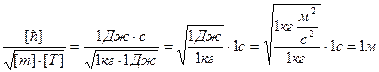 .
.
Найденная единица является единицей длины.
Произведем вычисления:
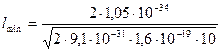 = 1,24 10-10 м = 124 нм.
= 1,24 10-10 м = 124 нм.
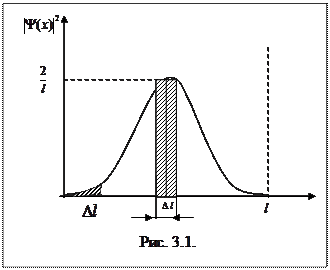 Пример 5. Волновая функция
Пример 5. Волновая функция 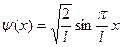 описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l, рис.3.1. Вычислить вероятность нахождения частицы в малом интервале Dl = 0,01 l в двух случаях:
описывает основное состояние частицы в бесконечно глубоком прямоугольном ящике шириной l, рис.3.1. Вычислить вероятность нахождения частицы в малом интервале Dl = 0,01 l в двух случаях:
1) (вблизи стенки) (0£ x £ Dl);
2) в средней части ящика (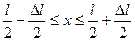 ).
).
 2015-04-01
2015-04-01 9139
9139
